Teil C – Experimente

Hinweis: Von den nachfolgenden Wahlaufgaben C 1 und C 2 soll in der Prüfung nur eine bearbeitet werden.

Wahlaufgabe C 1: Brechung des Lichtes

Führe Messungen und Berechnungen zur Brechung eines Lichtbündels an einem geraden gleichseitigen optischen Prisma durch.
Alle notwendigen Geräte und Hilfsmittel sind am Arbeitsplatz bereitgestellt.

Plane das Experiment den folgenden Aufgabenstellungen gemäß.
Das planvolle und systematische Experimentieren wird bewertet.

Erreichbare BE-Anzahl: 01

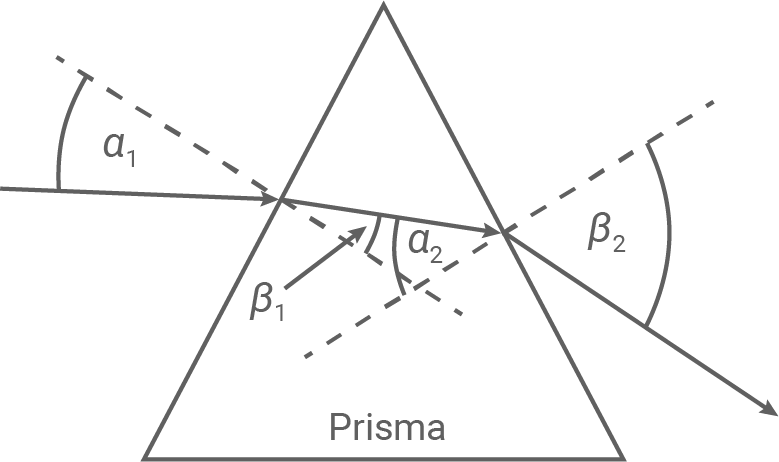
Das Prisma steht auf einer seiner beiden dreieckigen Grundflächen auf einem Blatt Kopierpapier. Ein schmales paralleles Lichtbündel verläuft parallel zum Blatt und trifft aus Luft kommend auf die Seitenfläche des Prismas, durchläuft dieses und tritt wieder in Luft aus.

Die Abbildung zeigt das Prinzip.

sachsen physik abi gk 2021 teil c1 abbildung 1 prisma

Vom Aufsicht führenden Lehrer wird dir ein Kopierpapierblatt (A4) bereitgestellt, auf dem zweimal der Umriss der Grundfläche des Prismas in Originalgröße und das Einfallslot abgebildet sind.
Stelle das Prisma auf eine der beiden Umrisse und baue die Experimentieranordnung auf. Beobachte den Verlauf des Lichtbündels. Wähle einen Einfallswinkel $\alpha_1$ so, dass das auf der anderen Seite des Prismas austretende Lichtbündel deutlich zu erkennen ist.

1.1

Zeichne in den Umriss den Verlauf des Lichtbündels ein.
Miss den Einfallswinkel $\alpha_1$ und den zugehörigen Brechungswinkel $\beta_1$ .
Wiederhole das Experiment für einen anderen Einfallswinkel.

Erreichbare BE-Anzahl: 04

1.2

Berechne die Brechzahl $n$ des Stoffes, aus dem das Prisma besteht.

Erreichbare BE-Anzahl: 02

Die Brechzahl des Stoffes soll nun durch ein anderes experimentelles Vorgehen ermittelt werden. Stelle das Prisma auf den anderen Umriss. Wähle den Einfallswinkel $\alpha_1$ so, dass der Brechungswinkel $\beta_2$ genau $90^{\circ}$ beträgt.

2.1

Zeichne den Verlauf des Lichtbündels ein. Miss den Winkel $\alpha_2$ .

Erreichbare BE-Anzahl: 03

2.2

Zeige, dass unter der Bedingung $\beta_2=90^{\circ}$ gilt: $\sin \alpha_2=\dfrac{1}{n}$ .
Berechne die Brechzahl $n$ des Stoffes, aus dem das Prisma besteht.

Erreichbare BE-Anzahl: 03

Gib je einen systematischen und einen zufälligen Fehler an, der bei der Ermittlung der Brechzahl auftritt.

Erreichbare BE-Anzahl: 02

Wahlaufgabe C 2: Mechanik - Bewegung und Energie

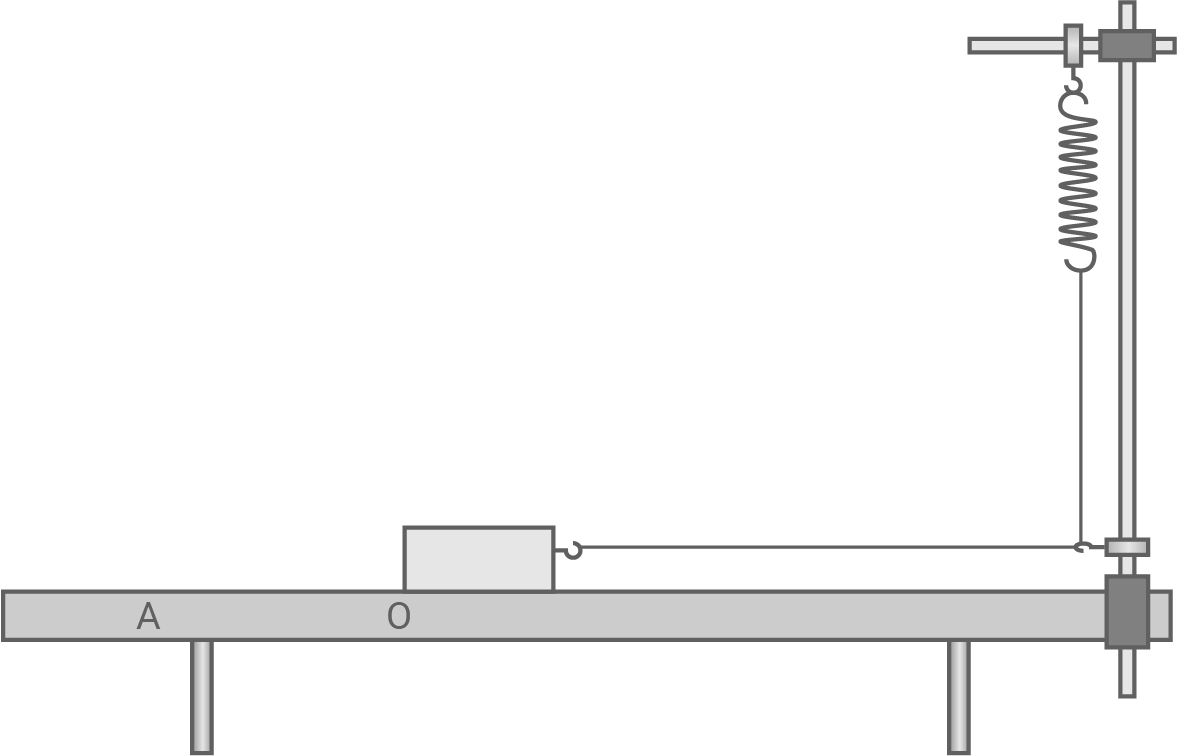
Führe Untersuchungen an einem mechanischen System durch. Das System besteht aus einer Feder und einem Gleitkörper, die über einen Faden verbunden sind. Die Abbildung zeigt das Prinzip der Experimentieranordnung.

sachsen physik abi gk 2021 teil c2 abbildung 1 mechanisches system mit feder, gleitkörper und faden

Die vollständig aufgebaute Experimentieranordnung sowie alle erforderlichen Geräte und Hilfsmittel werden dir am Arbeitsplatz bereitgestellt.

Plane das Experiment den folgenden Aufgabenstellungen gemäß.

Das planvolle und systematische Experimentieren wird bewertet.

Erreichbare BE-Anzahl: 01

Miss die Länge der Strecke $\overline{\text{OA }}$ .
Löse den Faden von der Feder. Miss für vier verschiedene Dehnungskräfte jeweils die Längenänderung $\Delta \ell$ .
Ermittle unter Nutzung aller Messwertpaare die Federkonstante $\text D$ .

Hinweise: Für die Feder gilt $\text F=\text D \cdot \Delta \ell$ .
Die maximale Dehnung der Feder entspricht der Strecke $\overline{\text{OA }}$ .

Erreichbare BE-Anzahl: 05

Befestige den Faden wieder an der Feder. Lege den Gleitkörper an den Ort O. An diesem Ort ist die Feder gerade noch nicht gespannt. Ziehe den Gleitkörper auf der horizontalen Ebene nach links, bis sich dessen hinteres Ende am Ort A befindet. Die Feder wird dabei um die Länge der Strecke $\overline{\text{OA }}$ gedehnt.

2.1

Gib den Gleitkörper frei und miss den von diesem bis zum Stillstand zurückgelegten Weg.

Erreichbare BE-Anzahl: 02

2.2

Berechne die Energie der gespannten Feder $E_{ sp }.$

Erreichbare BE-Anzahl: 02

2.3

Die gesamte Spannenergie wird durch Reibungsarbeit entwertet.
Berechne die mittlere Reibungskraft für die Bewegung des Gleitkörpers.

Erreichbare BE-Anzahl: 02

Entferne den Faden vom Gleitkörper

3.1

Ziehe den Gleitkörper unter Nutzung eines Federkraftmessers gleichförmig auf der horizontalen Ebene. Miss die Reibungskraft.

Erreichbare BE-Anzahl: 01

3.2

Vergleiche die Reibungskräfte aus den Teilaufgaben 2.3 und 3.1.
Diskutiere das Ergebnis des Vergleichs.

Erreichbare BE-Anzahl: 02

Lösung C 1: Brechung des Lichtes

1.1

Die Messungen der eingezeichneten Winkel mit einem Geodreick liefern beispielsweise folgende Werte:

$\color{#ffffff}{\alpha_1}$	$\color{#ffffff}{\beta_1}$
30 °	18,5 °
70 °	38,5 °

1.2

Mit dem snelluischen Brechungsgesetz folgt für den Brechungsindex $n_2$ des Prismas:

Rechenweg anzeigen

$n=\dfrac{n_{\text{Luft}} \cdot \sin(\alpha_1)}{\sin(\beta_1)}$

Einsetzen der Werte lifert für die erste Messung:

$\(\begin{array}[t]{rll} n$

Für die zweite Messung folgt:

$\(\begin{array}[t]{rll} n$

Der Mittelwert der beiden errechneten Brechungsindizes liefert:

$\(\begin{array}[t]{rll} \overline{n_2}&=& \dfrac{n$

2.1

Stelle das Prisma auf den anderen Umriss auf dem Papier, so dass eine der dreieckigen Grundflächen auf dem Umriss liegt.
Wähle den Einfallswinkel $\alpha_1$ so, dass der Brechungswinkel $\beta_2$ genau $90^\circ$ beträgt. Das bedeutet, dass das Licht senkrecht zur zweiten Grundfläche des Prismas eintritt und somit parallel zur Oberfläche gebrochen wird. Der Winkel $\alpha_1$ muss bei diesem Prisma etwa $28°$ betragen, damit der Winkel $\beta_2=90°.$
Messen des Winkels $\alpha_2$ liefert etwa $42°.$

2.2

Zusammenhang für $\sin\left(\alpha_2\right)$

Mit dem snelluischen Brechnungsgesetz folgt:

$\begin{array}[t]{rll} n\cdot \sin\left(\alpha_2 \right) &=& n_{\text{Luft}}\cdot \sin{\left(\beta_2\right)}&\quad \scriptsize \mid\; \cdot \dfrac{1}{n}\\[5pt] \sin\left(\alpha_2 \right) &=& \dfrac{n_{\text{Luft}}\cdot \sin{\left(\beta_2\right)}}{n} \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} \sin\left(\alpha_2 \right)&=& \dfrac{n_{\text{Luft}}\cdot \sin{\left(\beta_2\right)}}{n}&\quad \scriptsize \\[5pt] &=&\dfrac{1\cdot \sin{\left(90°\right)}}{n}&\quad \scriptsize \\[5pt] &=&\dfrac{ 1}{n}&\quad \scriptsize \\[5pt] \end{array}$

Berechnung des Brechungsindex n

$\begin{array}[t]{rll} \sin\left(\alpha_2 \right)&=&\dfrac{ 1}{n}&\quad \scriptsize \mid\, \left(\,\right)^{-1}\\[5pt] \dfrac{1}{\sin\left(\alpha_2 \right)}&=& n&\quad \scriptsize \\[5pt] n&=& \dfrac{1}{\sin\left(\alpha_2 \right)} \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} n&=& \dfrac{1}{\sin\left(\alpha_2 \right)}&\quad \scriptsize \\[5pt] &=& \dfrac{1}{\sin\left(42° \right)}&\quad \scriptsize \\[5pt] &=& 1,5 \end{array}$

Eine mögliche systematische Fehlerquelle könnte sein, dass das Prisma nicht exakt auf dem vorgezeichneten Umriss platziert wird. Dadurch könnten die gemessenen Winkelabweichungen systematisch verfälscht werden, da das Licht nicht korrekt durch das Prisma gebrochen wird.

Ein zufälliger Fehler könnte durch die begrenzte Genauigkeit der Messinstrumente entstehen, wie zum Beispiel durch die Ableseungenauigkeit des Winkelmessers. Dies kann zu zufälligen Schwankungen in den gemessenen Werten führen.

Lösung C2: Mechanik – Bewegung und Energie

1.1

Messen der Strecke $\overline{OA}$ ergibt beispielsweise $\overline{OA}= 15 \;\text{cm}.$

Messungen für verschiedene Dehnungskräfte

Es ergeben sich beispielsweise folgende Werte:

$\color{#ffffff}{F}$ in $\color{#ffffff}{\text{N}}$	$\color{#ffffff}{\Delta \ell}$	$\color{#ffffff}{D}$ in $\color{#ffffff}{\frac{\text{N}}{\text{m}}}$
10	0,5	20
50	2	25
100	4	25
150	6	25

Die Federkonstante $D$ für die einzelnen Messwertpaare wird jeweils in der Tabelle durch $D= \dfrac{F}{\Delta \ell}$ berechnet.

Federkonstante aller Messwertpaare

Mittelwertbildung ergibt:

$\dfrac{20+25+25+25+25}{4}= \dfrac{95}{4} \approx 23,75$

Daraus folgt die Federkonstante zu $D \approx 23,75 \;\frac{\text{N}}{\text{m}}.$

2.1

Nach dem Loslassen, schwingt der Körper zunächst hin und her, bis er schließlich zum Stillstand kommt, wenn die Feder in Ruhelage ist.

$\Delta s = \overline{OA}= 15 \;\text{cm}$

2.2

Es gilt:

$\begin{array}[t]{rll} E_{\text{Sp}}&=& \frac{1}{2} \cdot D\cdot \Delta s^2 \\[5pt] &=& \frac{1}{2} \cdot 23,75 \;\frac{\text{N}}{\text{m}}\cdot (0,15 \;\text{m})^2 \\[5pt] &=&0,2671 \;\text{J} \end{array}$

2.3

Die Spannenergie wird umgewandelt in kinetische Energie und Reibungsarbeit.

Der Körper schwingt solange, bis alle kinetische Energie in Reibungsarbeit umgewandelt ist. Beim Stillstand ist die Spannenergie vollständig durch Reibungsarbeit entwertet.

Um die mittlere Reibungskraft $F_R$ zu berechnen, kann vereinfacht folgende Energiegleichung aufgestellt werden:

Rechenweg anzeigen

$E_{\text{Sp}}=1,79 \;\text{N}$

3.1

Der Kraftmesser zeigt ca. $F_{\text{mess}}=0,5 \;\text{N}.$

Es gilt:

$\begin{array}[t]{rll} F_{\text{mess}}&=& F-F_R &\quad \scriptsize \mid\;-F \\[5pt] F_{\text{mess}}-F&=& -F_R \\[5pt] F_R&=& F-F_{\text{mess}} \\[5pt] F_R&=& m\cdot g -F_R \end{array}$

Vom Gleitkörper wird die Masse abgelesen. Sie beträgt beispielsweise $m=0,2 \;\text{kg}.$

$\begin{array}[t]{rll} F_R&=&0,2 \;\text{kg} \cdot 9,81\;\frac{\text{N}}{\text{kg}} -0,5 \\[5pt] &=& 1,462 \;\text{N} \end{array}$

3.2

Die Differenz der Reibungskräfte beträgt $1,79 \;\text{N}- 1,462 \;\text{N} =0,328\;\text{N}.$

Die mittlere Reibungskraft hat einen größeren Betrag, da sie im Schwingsystem mit der Feder aufgrund der kinetischen Energie nur im Mittel bestimmbar ist.

Bei der Bestimmung Reibungskraft auf horizontaler Ebene können Fehler entstehen durch das Ablesen vom Kraftmesser und der Ausführung der gleichförmigen Bewegung.