Teil B – Bewegungen, Optik
1
Bewegungen
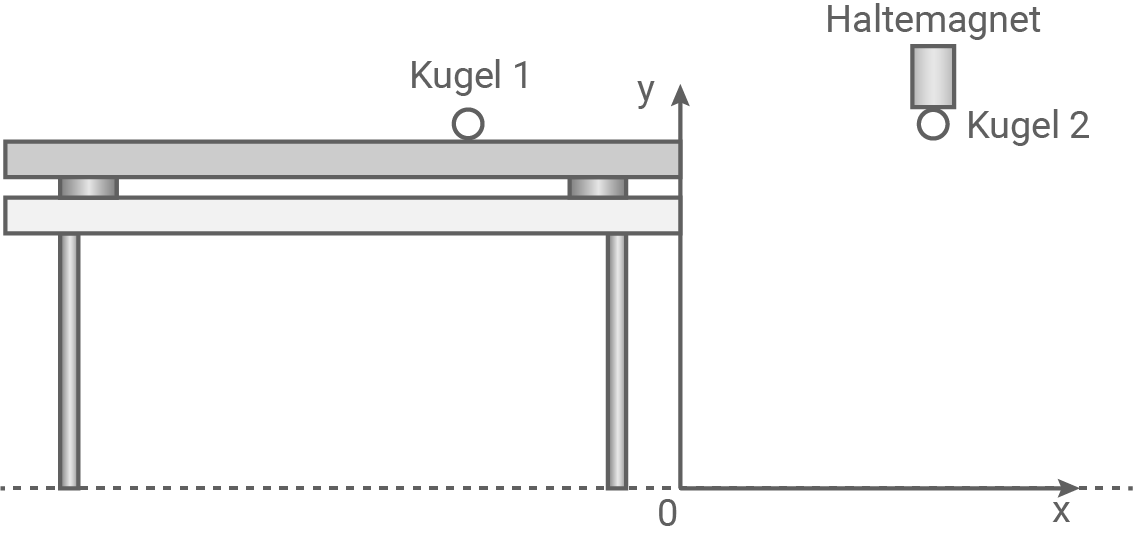
Die Bewegungen zweier gleicher Kugeln werden betrachtet. Beide Kugeln werden als Massepunkte betrachtet. Reibungseinflüsse werden vernachlässigt.

1.1
Kugel 1 bewegt sich geradlinig auf einer waagerechten Schiene. Zum Zeitpunkt  verlässt die Kugel am Ort
verlässt die Kugel am Ort  die Schiene mit der Geschwindigkeit
die Schiene mit der Geschwindigkeit  . Sie durchläuft den Punkt
. Sie durchläuft den Punkt  und trifft zum Zeitpunkt
und trifft zum Zeitpunkt  im Punkt
im Punkt  auf der Unterlage auf.
auf der Unterlage auf.
1.1.1
Ermittle die Koordinaten  und
und  .
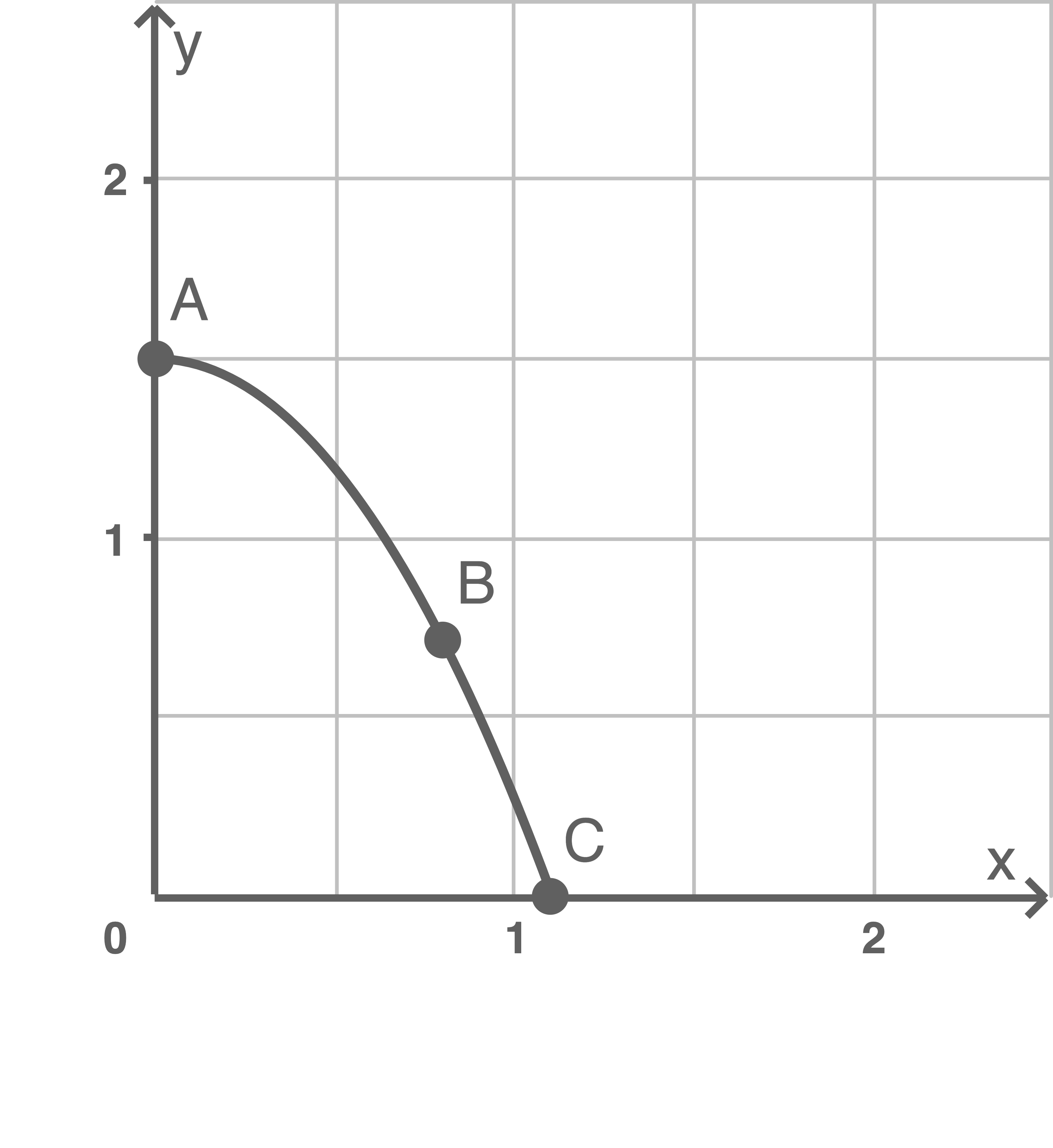
Trage die Punkte
.
Trage die Punkte 
 und
und  in ein Koordinatensystem ein und zeichne die Wurfparabel für Kugel 1 ein.
in ein Koordinatensystem ein und zeichne die Wurfparabel für Kugel 1 ein.
Erreichbare BE-Anzahl: 06
1.1.2
Ermittle den Betrag der Auftreffgeschwindigkeit für Kugel 1.
Erreichbare BE-Anzahl: 02
1.2
Kugel 2 befindet sich am Ort  an dem Haltemagnet.
an dem Haltemagnet.
1.2.1
Der waagerechte Wurf wird wiederholt. Gib an, zu welchem Zeitpunkt der Haltemagnet Kugel 2 freigeben muss, so dass beide Kugeln gleichzeitig den Ort  durchlaufen. Begründe unter Nutzung des Superpositionsprinzips.
durchlaufen. Begründe unter Nutzung des Superpositionsprinzips.
Erreichbare BE-Anzahl: 03
1.2.2
Berechne den Zeitpunkt  , zu dem beide Kugeln den Ort
, zu dem beide Kugeln den Ort  durchlaufen.
durchlaufen.
Erreichbare BE-Anzahl: 02
2
Optik
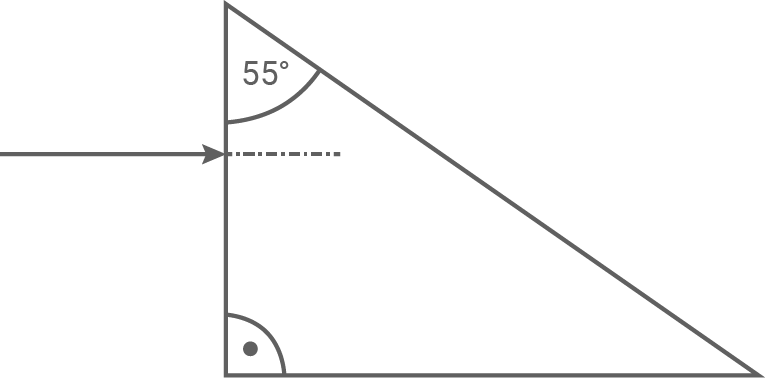
Ein gerades Prisma mit rechtwinkligem Dreieck als Grundfläche besteht aus Glas der Brechzahl 1,46. Ein schmales, paralleles Bündel monochromatischen Lichts trifft aus Luft kommend senkrecht auf eine Seitenfläche des Prismas.
Die nachfolgende Abbildung zeigt das Prinzip.

2.1
Das Lichtbündel durchläuft das Prisma und tritt wieder in Luft aus.
2.1.1
Die Brechung von Licht lässt sich mit dem Huygens'schen Prinzip erklären. Nenne Grundaussagen dieses Prinzips.
Erreichbare BE-Anzahl: 02
2.1.2
Berechne die Geschwindigkeit, mit der sich das Licht im Glas ausbreitet.
Erreichbare BE-Anzahl: 02
2.1.3
Übernimm die Abbildung maßstäblich. Zeichne den weiteren Verlauf des Lichtwegs ein. Gib deinen Lösungsweg einschließlich aller erforderlichen Berechnungen an.
Erreichbare BE-Anzahl: 06
2.2
Eine Glühlampe sendet weißes Licht aus, dieses enthält alle Wellenlängen im Intervall  Ein schmales paralleles Bündel dieses Lichts fällt senkrecht auf ein optisches Gitter der Gitterkonstante
Ein schmales paralleles Bündel dieses Lichts fällt senkrecht auf ein optisches Gitter der Gitterkonstante  . Im Abstand
. Im Abstand  ist parallel zur Gitterebene ein Schirm angeordnet, auf dem links und rechts neben einem schmalen weißen Streifen jeweils ein Band kontinuierlich verteilter Spektralfarben zu sehen ist. Beide Farbbänder sind symmetrisch zum weißen Streifen angeordnet.
ist parallel zur Gitterebene ein Schirm angeordnet, auf dem links und rechts neben einem schmalen weißen Streifen jeweils ein Band kontinuierlich verteilter Spektralfarben zu sehen ist. Beide Farbbänder sind symmetrisch zum weißen Streifen angeordnet.
2.2.1
Erkläre die spektrale Zerlegung des weißen Lichts für das beschriebene Experiment.
Erreichbare BE-Anzahl: 03
2.2.2
Berechne die Breite eines der Farbbänder.
Erreichbare BE-Anzahl: 04
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
Die Bewegung der Kugel 1 lässt sich in zwei Bewegungen aufteilen:
Bestimmung der
Gegeben: 


 Gesucht:
Gesucht:  Lösung:
1. Schritt: Zeit
Lösung:
1. Schritt: Zeit  bestimmen, in der Kugel den Punkt B durchläuft
In
bestimmen, in der Kugel den Punkt B durchläuft
In  -Richtung gilt:
-Richtung gilt:
![\(\begin{array}[t]{rll}
x_B&=& v_x\cdot t_B &\quad \scriptsize \mid\;\cdot \dfrac{1}{v_x}\\[5pt]
\dfrac{x_B}{v_x}&=& t_B &\quad \scriptsize \\[5pt]
t_B &=&\dfrac{x_B}{v_x} &\quad \scriptsize \\[5pt]
t_B &=&\dfrac{0,80 \,\text{m}}{2,00 \,\frac{\text{m}}{\text{s}}} &\quad \scriptsize \\[5pt]
t_B &=& 0,4 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/6eaf2b838daf0ebbd98374bd0c18f1969c744da50ce4f7767ec22c56d9fbdfc3_light.svg) 2. Schritt: Ortskoordinate
2. Schritt: Ortskoordinate  bestimmen
Einsetzen von
bestimmen
Einsetzen von  in die Ortsgleichung für die Bewegung in
in die Ortsgleichung für die Bewegung in  -Richtung liefert
-Richtung liefert 
 Einsetzen der Werte:
Einsetzen der Werte:
![\(\begin{array}[t]{rll}
y(t_B)&=& -\dfrac{1}{2}\cdot 9,81 \;\frac{\text{m}}{\text{s}^2} \cdot (0,4 \;\text{s})^2+1,50 \,\text{m}&\quad \scriptsize \\[5pt]
&=& 0,7152 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/4c577cc7659479f7bf9bfa63b0f81f79b36b5f3338c31300561d5c1a61b37880_light.svg)
Bestimmung der
Gegeben: 


 Gesucht:
Gesucht:  Lösung:
1. Schritt: Zeitpunkt
Lösung:
1. Schritt: Zeitpunkt  bestimmen
Werte einsetzen:
bestimmen
Werte einsetzen:
![\(\begin{array}[t]{rll}
t_C&=&\sqrt{\dfrac{2\cdot 1,5\;\text{m}}{9,81 \;\frac{\text{m}}{\text{s}^2}}} \\[5pt]
t_C&\approx& 0,56 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/3e7eb92d1d42dbac9213b90b4186e8d924056512772ae5ed83922aaf1c92253b_light.svg) 2. Schritt:
2. Schritt:  in die Ortsgleichung für die Bewegung in
in die Ortsgleichung für die Bewegung in  -Richtung einsetzen
-Richtung einsetzen
![\(\begin{array}[t]{rll}
x_C&=& v_x \cdot t_C &\quad \scriptsize \\[5pt]
x_C&=& 2,00 \,\dfrac{\text{m}}{\text{s}} \cdot 0,56 \;\text{s} &\quad \scriptsize \\[5pt]
&=& 1,1 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/8ceb6b3d79bd0b9e5c243b661f3f434f3cdb482a9da0f808f1451f00c4bed282_light.svg)
- gleichförmige Bewegung in
-Richtung:
- gleichmäßig beschleunigte Bewegung in
-Richtung:
Bestimmung der  -Koordinate
-Koordinate
Gegeben: Bestimmung der  Koordinate
Koordinate
Gegeben: 
1.1.2
Gegeben: 

 Gesucht:
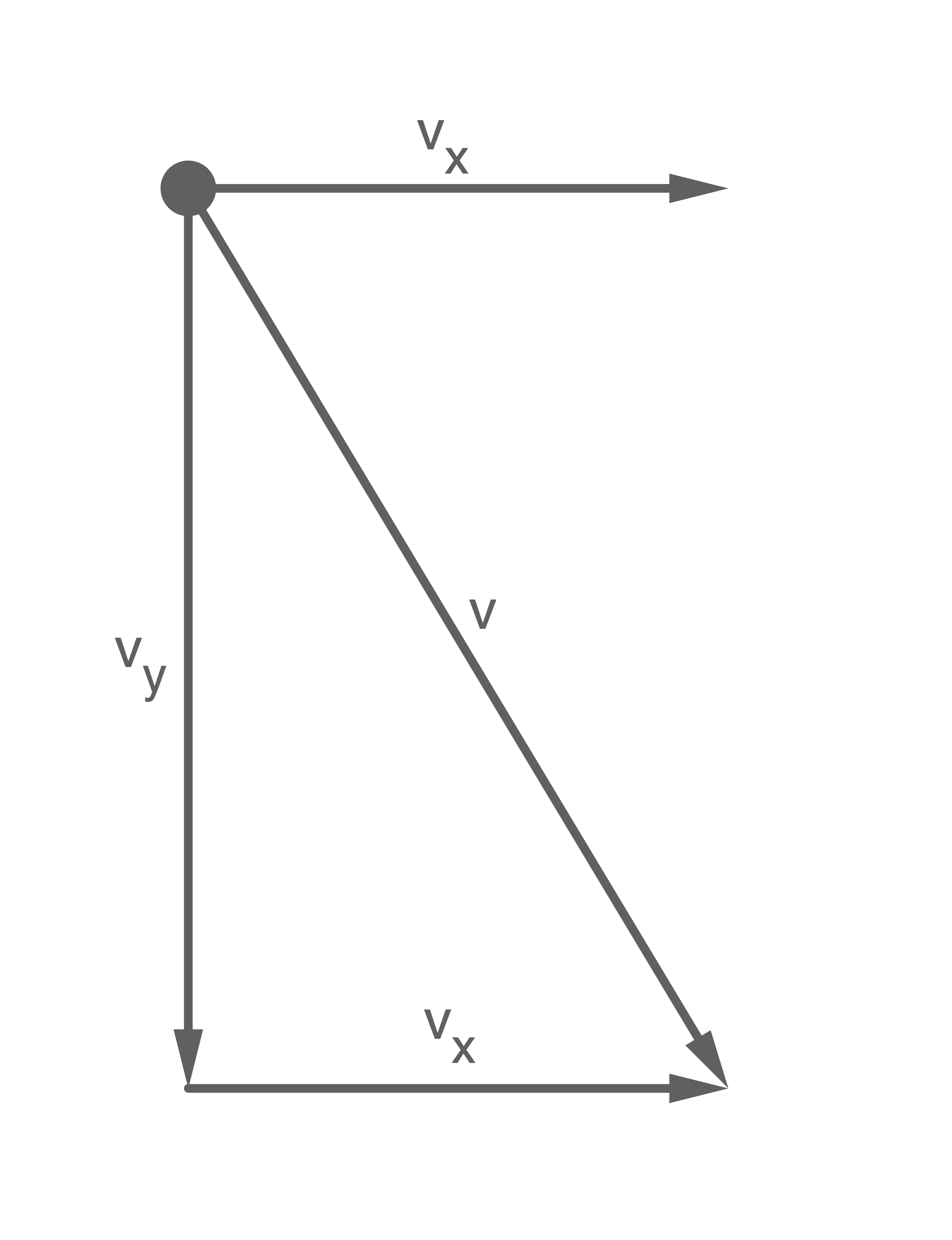
Gesucht:  Lösung: Der Betrag der Auftreffgeschwindigkeit
Lösung: Der Betrag der Auftreffgeschwindigkeit  kann aus den Geschwindigkeitskomponenten
kann aus den Geschwindigkeitskomponenten  und
und  berechnet werden. Diese ergänzen sich zu einem rechtwinkligen Dreieck für das mit dem Pythagoras folgt:
berechnet werden. Diese ergänzen sich zu einem rechtwinkligen Dreieck für das mit dem Pythagoras folgt:
![\(\begin{array}[t]{rll}
v^2&=& v_x^2+v_y^2&\quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
v&=&\sqrt{v_x^2+v_y^2}
\end{array}\)](https://www.schullv.de/resources/formulas/5b017e16c77ec5b6f829cb7e91a884472a8ae191eae57e876ae8a95cecd1e1ee_light.svg)
1.2.1
Kugel 2 wird zur selben Zeit freigegeben werden wie Kugel 1.
An Kugel 1 wirken zwei gleichzeitig wirkende Kräfte: die senkrecht nach unten gerichtete Gewichtskraft und die horizontale Kraft aufgrund des waagerechten Wurfs. Die waagrechte Bewegung der Kugel 1 verursacht keine Höhenänderung, sodass beide Kugeln stets auf gleicher Höhe bleiben.
Gemäß dem Superpositionsprinzip überlagern sich die Kräfte in - und in
- und in  -Richtung, ohne sich gegenseitig zu beeinflussen. Deswegen erreichen beide Kugeln nach gleicher Zeit den Punkt B, da sie aus derselben Höhe starten.
-Richtung, ohne sich gegenseitig zu beeinflussen. Deswegen erreichen beide Kugeln nach gleicher Zeit den Punkt B, da sie aus derselben Höhe starten.
Gemäß dem Superpositionsprinzip überlagern sich die Kräfte in
1.2.2
Der Zeitpunkt  an dem die Kugeln den Punkt B durchlaufen, lässt sich entweder über die senkrechte Bewegung der Kugel 1 bzw. 2 oder über die horizontale Bewegung der Kugel 1 berechnen.
Mit der horizontalen Bewegung der Kugel 1 ergibt sich für
an dem die Kugeln den Punkt B durchlaufen, lässt sich entweder über die senkrechte Bewegung der Kugel 1 bzw. 2 oder über die horizontale Bewegung der Kugel 1 berechnen.
Mit der horizontalen Bewegung der Kugel 1 ergibt sich für 
![\(\begin{array}[t]{rll}
x_B&=& v_x\cdot t_B &\quad \scriptsize \mid\; \dfrac{1}{v_x}\\[5pt]
\dfrac{x\left(t_B\right)}{v_x}&=& t_B &\quad \scriptsize\\[5pt]
t_B&=&\dfrac{x_B}{v_x}
\end{array}\)](https://www.schullv.de/resources/formulas/31156a80cc5e69686fce2c43bf3040b3bed43c3f9e02405976f175f483de42d1_light.svg) Werte einsetzen:
Werte einsetzen:
![\(\begin{array}[t]{rll}
t_B&=& \dfrac{0,80 \,\text{m}}{2\,\frac{\text{m}}{\text{s}}} &\quad \scriptsize \\[5pt]
&=& 0,4 \,\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/98ddd6492b9d5d2475151c2c2ed45446d27461a0e3d057423dc6d42015448340_light.svg)
2.1.1
- Jeder Punkt einer Wellenfront (Punkte mit gleicher Phase) lässt sich als Ausgangspunkt einer Elementarwelle betrachten.
- Wellenfronten lassen sich als Einhüllende dieser Elementarwellen darstellen.
- Die Elementarwellen haben immer gleiche Frequenz und Wellenlänge wie die Welle, aus der sie entstanden sind oder die sie erzeugen.
2.1.2
Für die Brechung von Licht gilt:
![\(\begin{array}[t]{rll}
n_{\text{Brechzahl}}&=& \dfrac{c_\text{Luft}}{c_\text{Glas}}&\quad \scriptsize \mid\; \cdot \dfrac{c_\text{Glas}}{n_{\text{Brechzahl}}} \\[5pt]
c_\text{Glas} &=& \dfrac{c_\text{Luft}}{n_{\text{Brechzahl}}}
\end{array}\)](https://www.schullv.de/resources/formulas/97aab75a08df5df4e08d8b483d0338294dde40a15d3965cbc428c2bd75b3ac25_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
c_\text{Glas} &=& \dfrac{c_\text{Luft}}{n_{\text{Brechzahl}}}&\quad \scriptsize \\[5pt]
&=& \dfrac{3\cdot 10^8 \,\dfrac{\text{m}}{\text{s}}}{1,46} &\quad \scriptsize \\[5pt]
&=& 2 \cdot 10^8 \,\dfrac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/b0157d888969c12400f49168f65c8cdcc9677d00f78c32bf4a12720e3420c81d_light.svg)
2.1.3
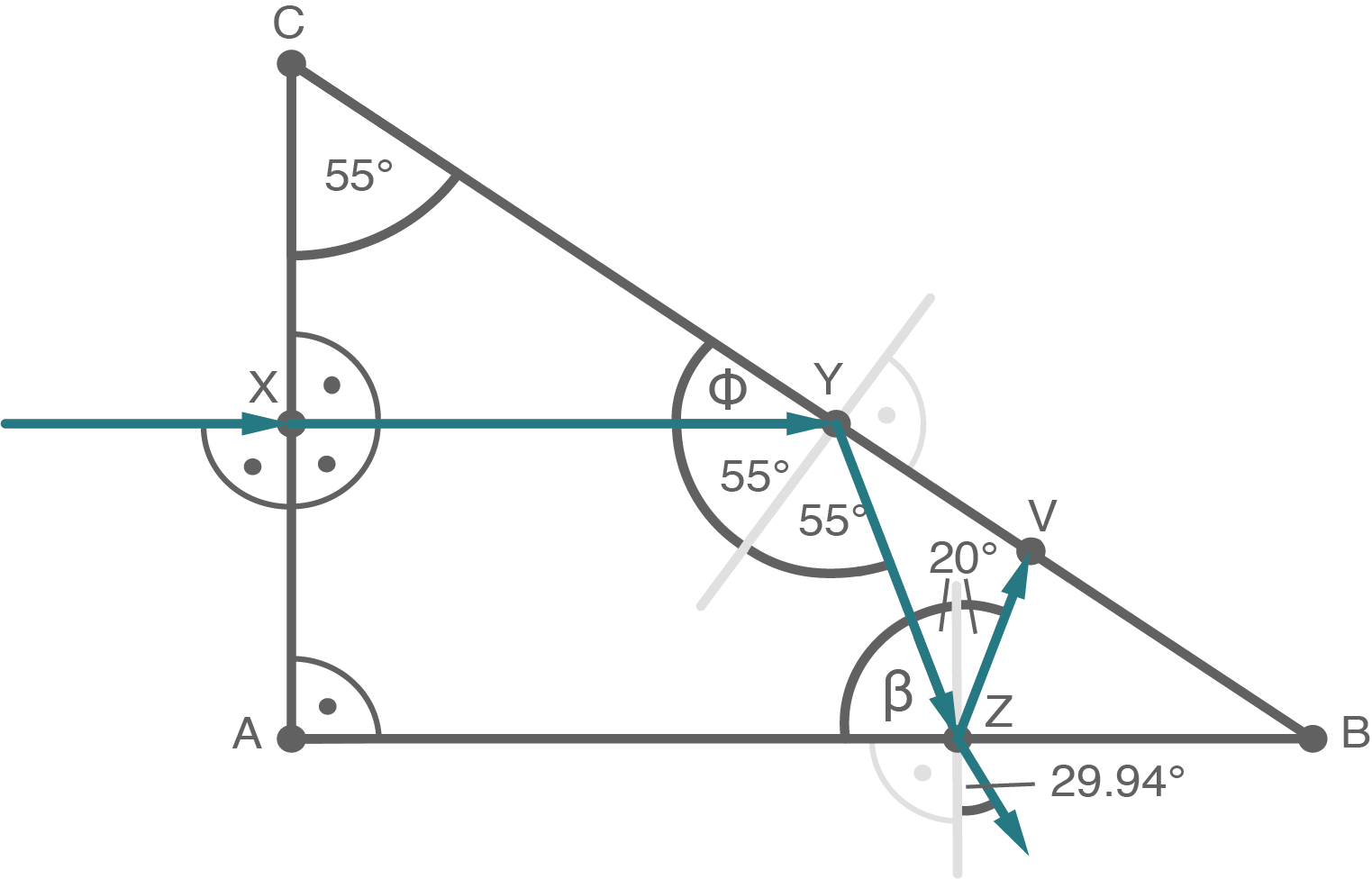
2.2.1
Hinter dem Gitter entstehen Elementarwellen verschiedener Spektralfarben, die miteinander interferieren. Bei bestimmten Gangunterschieden zwischen diesen entstehen Intensitätsmaxima und Intensitätsminima. Die Abstände zwischen den Maxima variieren je nach Wellenlänge, wobei kürzere Wellenlängen kleinere Abstände verursachen. Dies führt zur Zerlegung des weißen Lichts, da es die Überlagerung von Licht mit unterschiedlichen Wellenlängen ist.
Der weiße Streifen in der Schirmmitte entsteht durch gleichzeitige Maxima aller Farben, da der Gangunterschied dort für jede Wellenlänge null ist. Links und rechts zeigen sich Farbbänder, beginnend mit der kürzesten Wellenlänge.
2.2.2
Um die Länge eines Farbbandes zu bestimmen, muss berechnet werden, wann die Farbe mit der kürzesten und mit der längsten Wellenlänge ihr erstes Intensitätsmaxima hat. Da die Gitterkonstante  viel kleiner ist als der Schirmabstand
viel kleiner ist als der Schirmabstand  gilt mit der Kleinwinkelnäherung:
Mit der Kleinwinkelnäherung gilt
gilt mit der Kleinwinkelnäherung:
Mit der Kleinwinkelnäherung gilt  und es folgt:
und es folgt:
![\(\begin{array}[t]{rll}
\tan{\left(\alpha\right)}&=& \dfrac{d_n}{a} &\quad \scriptsize \mid\;\tan{\left(\alpha\right)} \approx \alpha \\[5pt]
\alpha&=& \dfrac{d_n}{a}
\end{array}\)](https://www.schullv.de/resources/formulas/c086fce398d2ec3c762e6c0ad3d25ba50c0a7100bfd870e11e89db9f0ba78ab4_light.svg) Einsetzen in die Beugungsgleichung liefert:
Für die Wellenlänge
Einsetzen in die Beugungsgleichung liefert:
Für die Wellenlänge  folgt damit:
folgt damit:
![\(\begin{array}[t]{rll}
d_1&=& \dfrac{1 \cdot \lambda \cdot a}{g} \quad \scriptsize \\[5pt]
&=& \dfrac{1\cdot 390 \,\text{nm}\cdot 0,8\,\text{m}}{3\,\mu\text{m}}&\quad \scriptsize \\[5pt]
&=& 0,104 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/585ff664c5ff51901bda507a08959f112134711d5f7dbb5848863852e26fa240_light.svg) Für die Wellenlänge
Für die Wellenlänge  folgt damit:
folgt damit:
![\(\begin{array}[t]{rll}
d_1&=& \dfrac{1 \cdot \lambda \cdot a}{g} \quad \scriptsize \\[5pt]
&=&\dfrac{1\cdot 780 \,\text{nm} \cdot 0,8\,\text{m}}{3\,\mu\text{m}} &\quad \scriptsize \\[5pt]
&=& 0,208 \,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/bf54225dad584630eff449db735d91ee7156e74ea5f8a1059cd0f1999ca031db_light.svg) Die Länge eines Farbbandes ist somit die Differenz zwischen den Abständen der beiden Maxima:
Die Länge eines Farbbandes ist somit die Differenz zwischen den Abständen der beiden Maxima: 