Teil C – Experimente

Hinweis: Von den nachfolgenden Wahlaufgaben C 1 und C 2 soll in der Prüfung nur eine bearbeitet werden.

Wahlaufgabe C 1: Bewegung einer Kugel

Führe Untersuchungen zur Bewegung einer Kugel durch.
Die vollständig aufgebaute Experimentieranordnung sowie alle erforderlichen Geräte und Hilfsmittel werden dir vom Aufsicht führenden Lehrer übergeben.

Plane das Experiment den folgenden Aufgabenstellungen gemäß.

Das planvolle und systematische Experimentieren wird bewertet.

Erreichbare BE-Anzahl: 01

Die Kugel wird zum Zeitpunkt $t=0$ im Punkt A freigegeben, sie bewegt sich auf der Ablaufschiene eine geneigte Ebene hinab und durchläuft an deren Ende den Punkt B.

Die Abbildung zeigt das Prinzip der Experimentieranordnung.

sachsen physik abi gk 2022 teil c abbildung 1 prinzip der experimentieranordnung mit ablaufschiene

Die Kugel bewegt sich auf der geneigten Ebene geradlinig gleichmäßig beschleunigt. Beschreibe diese Bewegung bezüglich der Geschwindigkeit.

Erreichbare BE-Anzahl: 02

Die Kugel wird am Ort A freigegeben und legt auf der geneigten Ebene den Weg $\text s$ zurück.

2.1

Gib die Kugel am Ort A frei. Miss den Weg $\text s_{\max }=\overline{ AB }$ sowie die Zeit, die die Kugel zum Durchlaufen dieser Strecke benötigt.

Erreichbare BE-Anzahl: 02

2.2

Wiederhole das Experiment für drei weitere verschiedene Wege $0 \lt \text s \lt \text s_{\max }$ .

Erreichbare BE-Anzahl: 02

2.3

Zeichne unter Nutzung aller Messwertpaare aus 2.1 und 2.2 ein $s(t)$ -Diagramm.

Erreichbare BE-Anzahl: 02

2.4

Ermittle unter Nutzung aller Messwerte die Beschleunigung der Kugel für die Bewegung auf der Ablaufschiene. Berechne die Geschwindigkeit, die die Kugel im Punkt $B$ hat.

Erreichbare BE-Anzahl: 04

2.5

Für die Lösung dieser Teilaufgabe ist keine zusätzliche experimentelle Tätigkeit erforderlich.
Die Messungen aus 2.1 und 2.2 werden für eine größere Neigung der Ebene wiederholt. Die Länge der Strecke $\overline{ AB }$ bleibt gleich.
Skizziere den Graph $s(t)$ in das Diagramm aus Aufgabe 2.3.

Erreichbare BE-Anzahl: 02

Wahlaufgabe C 2: Spule im Gleich- und Wechselstromkreis

Führe Stromstärke- und Spannungsmessungen an einer Spule im Gleich- und Wechselstromkreis durch.
Forder beim Aufsicht führenden Lehrer alle benötigten Geräte und Hilfsmittel an.

Plane das Experiment den folgenden Aufgabenstellungen gemäß.

Das planvolle und systematische Experimentieren sowie das Anfordern der Geräte und Hilfsmittel werden bewertet.

Erreichbare BE-Anzahl: 02

Der Widerstand der Spule soll experimentell ermittelt werden.
Skizziere einen zugehörigen Schaltplan.

Erreichbare BE-Anzahl: 01

Widerstand im Gleichstromkreis

Erfrage beim Aufsicht führenden Lehrer die Einstellung der Spannungsquelle.
Baue die Schaltung auf.

2.1

Die Spule hat keinen Eisenkern.
Miss die Spannung über der Spule und die Stromstärke.
Berechne den Widerstand.

Erreichbare BE-Anzahl: 03

2.2

Die Spule hat einen geschlossenen Eisenkern.
Miss die Spannung über der Spule und die Stromstärke.
Berechne den Widerstand.

Erreichbare BE-Anzahl: 03

Widerstand im Wechselstromkreis

Der Widerstand der Spule ohne und der Widerstand mit geschlossenem Eisenkern sollen experimentell analog zu Aufgabe 2 ermittelt werden.
Erfrage beim Aufsicht führenden Lehrer die Einstellung der Spannungsquelle.
Führe alle erforderlichen Messungen durch und berechne die Widerstände.

Erreichbare BE-Anzahl: 04

Vergleiche das Verhältnis der Widerstände ohne und mit Eisenkern im Gleichstromkreis mit dem entsprechenden Verhältnis im Wechselstromkreis.
Gib die physikalische Ursache an.

Erreichbare BE-Anzahl: 02

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wahllösung C 1: Bewegung einer Kugel

Die Geschwindigkeit $v$ in der geradlinig gleichmäßig beschleunigten Bewegung der Kugel wird durch die Formel $v = a \cdot t$ beschrieben, wobei $a$ die konstante Beschleunigung und $t$ die Zeit ist. Das bedeutet, dass die Geschwindigkeit direkt proportional zur Zeit ist. Der Quotient $\frac{v}{t}$ bleibt konstant und entspricht der Beschleunigung $a.$

Anfangs ist die Geschwindigkeit der Kugel auf der geneigten Ebene null $(v_0 = 0),$ sie nimmt dann mit konstanter Rate zu, während die Kugel hinabrollt.

2.1

Messen der Strecke $\overline{\text{AB}}$ mit Hilfe eines Maßbandes ergibt beispielsweise $\overline{\text{AB}}=1,00 \;\text{m}$ mit dem absolute Messfehler $\Delta \overline{\text{AB}}=\pm\;0,05 \,\text{m}.$ Die Kugel benötigt beispielsweise $t_{\text{max}}=0,54 \;\text{s}.$ Der aboslute Messfehler der Zeit beträgt $\Delta t=\pm\;0,01 \;\text{s}.$

2.2

Für drei verschiedene Wege $s$ werden beispielsweise folgende Zeiten gemessen:

Messung	Strecke $\color{#fff}{s}$ in $\color{#fff}{\text{m}}$	Zeit $\color{#fff}{t}$ in $\color{#fff}{\text{s}}$
$s_1$	0,8	0,48
$s_2$	0,6	0,42
$s_3$	0,4	0,34

Der aboslute Messfehler der Zeit beträgt jeweils $\Delta t=\pm\;0,01 \;\text{s}.$

2.3

2.4

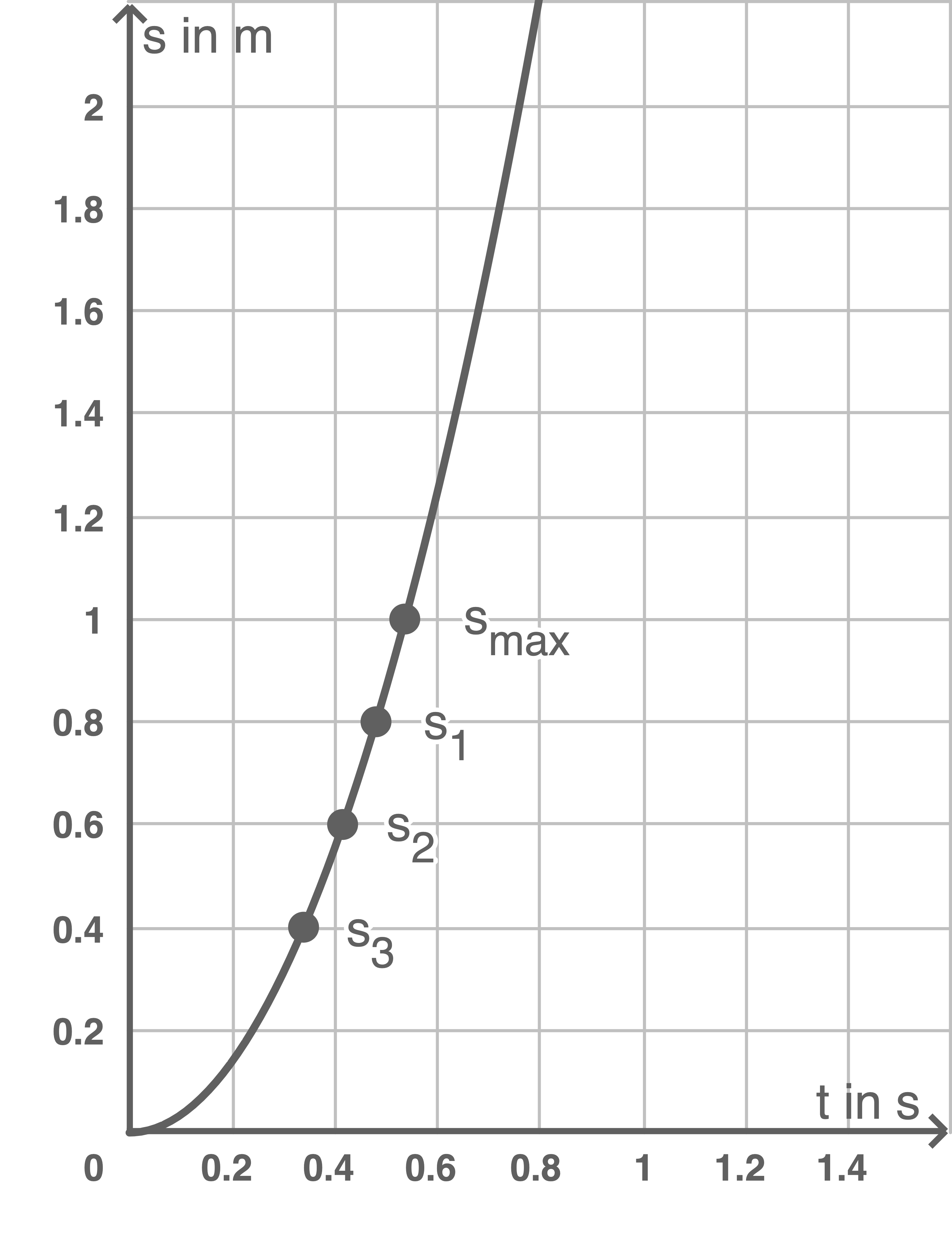
Berechnung der Beschleunigung $a$

Umstellen der Ortsgleichung der geradlinig gleichmäßig beschleunigte Kugel nach der Beschleunigung $a$ liefert:

$\begin{array}[t]{rll} s(t)&=&\dfrac{1}{2}\cdot a\cdot t^2 &\quad \scriptsize \mid\;\dfrac{a}{t^2} \quad t^2\neq 0\\[5pt] \dfrac{2\cdot s(t)}{t^2}&=& a &\quad \scriptsize \\[5pt] a &=& \dfrac{2\cdot s(t)}{t^2} \end{array}$

Einsetzen der jeweiligen Strecken $s_{\text{max}},s_1,s_2,s_3$ und der jeweils zugehörigen Zeiten $t_{\text{max}},t_1,t_2,t_3$ liefert die Beschleunigung $a:$

Messung	Strecke $\color{#fff}{s}$ in $\color{#fff}{\text{m}}$	Zeit $\color{#fff}{t}$ in $\color{#fff}{\text{s}}$
$s_{\text{max}}$	1,0	0,54
$s_1$	0,8	0,48
$s_2$	0,6	0,42
$s_3$	0,4	0,34

Für den Mittelwert der Beschleunigungen folgt damit:

Rechenweg anzeigen

$\overline{a}= 6,88 \,\dfrac{\text{m}}{\text{s}^2}$

Alternativer Lösungsweg: mit dem Streckungsfaktor der Parabel s(t)

Die Beschleunigung kann auch durch den Streckungsfaktor der Parabelfunktion aus den Messwerten im in Aufgabe 2.3 erstellten $s$ - $t$ -Diagramm berechnet werden. Die Ortsgleichung $s(t)$ ist eine Parabelfunktion, wobei für den Streckungsfaktor $b$ gilt:

$\begin{array}[t]{rll} b&=&\dfrac{1}{2}\cdot a &\quad \scriptsize \mid\;\cdot 2 \\[5pt] 2\cdot b&=& a &\quad \scriptsize \mid\;b= \dfrac{\Delta y}{(\Delta x)^2} \\[5pt] 2\cdot \dfrac{\Delta y}{(\Delta x)^2}&=& a &\quad \scriptsize \\[5pt] a &=& 2\cdot \dfrac{\Delta y}{(\Delta x)^2} \end{array}$

Für $\Delta y$ können die jeweiligen Strecken $s$ eingesetzt werden und für $\Delta x$ die zugehörigen Zeiten $t:$

$\begin{array}[t]{rll} a &=& 2\cdot \dfrac{s(t)}{t^2} \end{array}$

Messung	Strecke $\color{#fff}{s}$ in $\color{#fff}{\text{m}}$	Zeit $\color{#fff}{t}$ in $\color{#fff}{\text{s}}$
$s_{\text{max}}$	1,0	0,54
$s_1$	0,8	0,48
$s_2$	0,6	0,42
$s_3$	0,4	0,34

Für den Mittelwert der Beschleunigungen folgt damit:

Rechenweg anzeigen

$\overline{a}= 6,88 \,\dfrac{\text{m}}{\text{s}^2}$

Berechnung der Geschwindigkeit $v_B$

Für die Geschwindigkeit $v$ der geradlinig gleichmäßig beschleunigte Kugel, die an dem Punkt A losgelassen wurde, gilt:

$\begin{array}[t]{rll} v&=& a\cdot t_{\text{max}} +v_0 &\quad \scriptsize \mid\; v_0=0\\[5pt] &=& a\cdot t_{\text{max}} \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} v&=& a\cdot t_{\text{max}} &\quad \scriptsize \\[5pt] &=& 6,88 \,\dfrac{\text{m}}{\text{s}^2} \cdot 0,54 \,\text{s} &\quad \scriptsize \\[5pt] &=& 3,72 \,\dfrac{\text{m}}{\text{s}} \end{array}$

2.5

Parabel der Messwerte im s t Diagramm mit größerer Neigung

Erklärung (zum besseren Verständnis)

Aufgrund der Hangabtriebskraft der Kugel folgt für deren Beschleunigung:

$\begin{array}[t]{rll} F_H&=& m\cdot g\cdot \sin\left(\alpha\right) &\quad \scriptsize \mid\; F_H=m\cdot a \\[5pt] m\cdot a&=& m\cdot g\cdot \sin\left(\alpha\right) &\quad \scriptsize \mid\; \cdot \dfrac{1}{m} \\[5pt] a&=& g\cdot \sin\left(\alpha\right) \end{array}$

Da die Sinusfunktion für Werte zwischen $0°$ und $90°$ steigt, ist $a$ für einen größeren Neigungswinkel $\alpha$ größer als für einen kleineren. Eine größere Beschleunigung führt in der Parabelgleichung der Ortsgleichung $s(t) = \frac{1}{2} \cdot a \cdot t^2$ zu einem größeren Streckungsfaktor der Parabel. Die eingezeichnete Parabelfunktion muss folglich gestreckter sein als die Funktion, die durch die gemessenen Werte dargestellt wird.

Wahllösung C 2: Spule im Gleich- und Wechselstromkreis

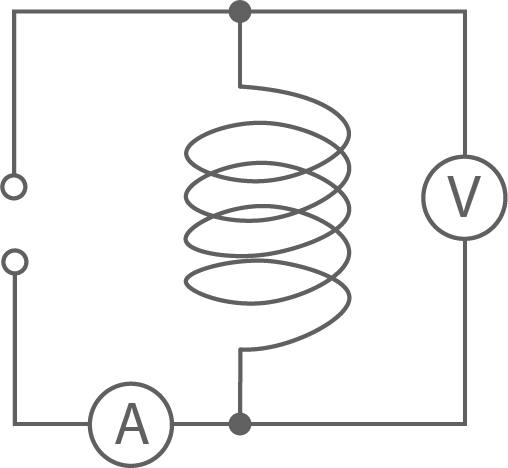Skizze des Schaltplans

Die Spule wird mit einer einstellbaren Gleichspannungsquelle verbunden, wobei die Spannung im zulässigen Bereich bleibt. Ein Voltmeter wird parallel zur Spule geschaltet, um die Spannung über die Spule zu messen. Ein Amperemeter wird in Reihe mit der Spule geschaltet, um die Stromstärke zu messen.

2.1

Die Spannung wird eingeschaltet und der angezeigte Stromwert (in Ampere) und der Spannungswert (in Volt) werden notiert. Zum Beispiel: $I=0,5 \, \text{A}$ und $U=5 \, \text{V}.$

Berechnung des Ohm'schen Widerstand $R$ mit Hilfe des Ohm'schen Gesetzes ergibt:

$\begin{array}[t]{rll} R&=& \dfrac{U}{I} &\quad \scriptsize \\[5pt] &=& \dfrac{5 \;\text{V}}{0,5 \;\text{A}} &\quad \scriptsize \\[5pt] &=& 10 \;\Omega \end{array}$

2.2

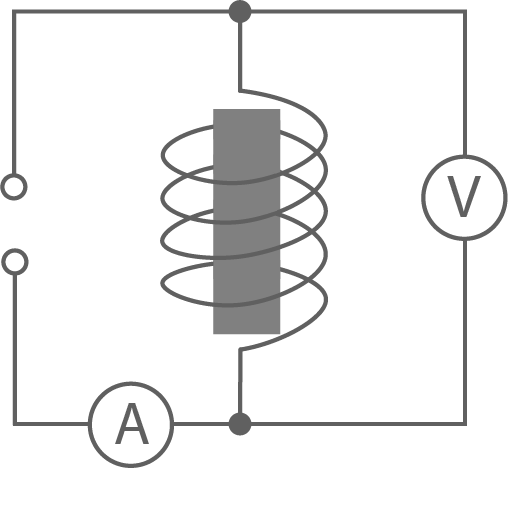Die Spannung wird eingeschaltet, und die angezeigten Strom- (in Ampere) und Spannungswerte (in Volt) werden notiert. Die Werte sollten nicht wesentlich von den zuvor gemessenen Werten bei der Spule ohne Eisenkern abweichen. Zum Beispiel: $I=0,45 \, \text{A}$ und $U=5 \, \text{V}.$

Berechnung des Ohm'schen Widerstand $R$ mit Hilfe des Ohm'schen Gesetzes ergibt:

$\begin{array}[t]{rll} R&=& \dfrac{U}{I} &\quad \scriptsize \\[5pt] &=& \dfrac{5 \;\text{V}}{0,48 \;\text{A}} &\quad \scriptsize \\[5pt] &=& 10,4 \;\Omega \end{array}$

3.1

Widerstand der Spule ohne Eisenkern

1. Schritt: Aufbau

Mögliche Schaltskizze

Die Spule wird mit einer Wechselspannungsquelle verbunden, wobei die Spannung im zulässigen Bereich bleibt.

Ein Voltmeter wird parallel zur Spule und zur Spannung geschaltet, um die Spannung über die Spule zu messen.

Ein Amperemeter wird in Reihe mit der Spule geschaltet, um die Stromstärke zu messen.

2. Schritt: Durchführung

Die Spannung wird eingeschaltet und der angezeigte Stromwert (in Ampere) und der Spannungswert (in Volt) werden notiert.
Alle Strom- und Spannungswerte, die gemessen werden sind Effektivwerte.

Beispielhafte Messergebnisse: $U=7 \, \text{V}$ und $I=45 \, \text{mA}.$

3. Schritt: Scheinwiderstand berechnen

Mittels Ohm'schen Gesetzes ergibt sich:

$\begin{array}[t]{rll} Z&=& \dfrac{U}{I} &\quad \scriptsize \\[5pt] &=& \dfrac{7 \;\text{V}}{0,045 \;\text{A}} &\quad \scriptsize \\[5pt] &\approx& 156 \;\Omega \end{array}$

Der elektrische Widerstand der Spule ist im Wechselstromkreis wesentlich größer als im Gleichstromkreis in Aufgabe 2. Die Selbstinduktion in einer Spule im Wechselstromkreis erzeugt eine Spannung, die der ursprünglichen Stromrichtung entgegenwirkt und diese abschwächt. Dadurch verhält sich die Spule ähnlich wie ein Widerstand.

Widerstand der Spule mit Eisenkern

1. Schritt: Aufbau

Mögliche Schaltskizze

In die Spule wird ein Eisenkern reingelegt. Der Rest des Versuchsaufbaus bleibt gleich.

2. Schritt: Durchführung

Die Spannung wird eingeschaltet und der angezeigte Stromwert (in Ampere) und der Spannungswert (in Volt) werden notiert.
Alle Strom- und Spannungswerte, die gemessen werden sind Effektivwerte.

Beispielhafte Messergebnisse: $U=7 \, \text{V}$ und $I=30 \, \text{mA}.$

3. Schritt: Scheinwiderstand berechnen

Mittels Ohm'schen Gesetzes ergibt sich:

$\begin{array}[t]{rll} Z&=& \dfrac{U}{I} &\quad \scriptsize \\[5pt] &=& \dfrac{7 \;\text{V}}{0,030 \;\text{A}} &\quad \scriptsize \\[5pt] &\approx& 233 \;\Omega \end{array}$

Der elektrische Widerstand einer Spule mit Eisenkern ist geringer als der einer Spule ohne Eisenkern, da die erhöhte magnetische Permeabilität des Eisenkerns den induktiven Widerstand verringert und somit zu einer Abnahme der effektiven Stromstärke führt.

$\begin{array}[t]{rll} \dfrac{R_{\text{ohne Eisenkern}}}{R_{\text{mit Eisenkern}}}&=& \dfrac{10 \,\Omega}{10,4 \,\Omega} &\quad \scriptsize \\[5pt] &=& 0.96 &\quad \scriptsize \\[5pt] &\approx& 1 \end{array}$

$\begin{array}[t]{rll} \dfrac{Z_{\text{ohne Eisenkern}}}{Z_{\text{mit Eisenkern}}}&=& \dfrac{156 \,\Omega}{233 \,\Omega} &\quad \scriptsize\\[5pt] &=& 0,7 \end{array}$

Im Gleichstromkreis bleibt der Widerstand einer Spule mit oder ohne Eisenkern weitgehend unverändert, da Selbstinduktionseffekte im Gleichstromkreis gering sind. Das Verhältnis der Widerstände ohne und mit Eisenkern ist daher nahe bei 1.

Im Wechselstromkreis erhöht der Eisenkern aufgrund seiner höheren magnetischen Permeabilität die Induktivität der Spule, was zu einem größeren induktiven Widerstand führt. Dies erhöht den gesamten Scheinwiderstand $Z$ , wodurch bei konstanter Spannung $U$ die Stromstärke $I$ abnimmt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?