Teil B – Mechanik, Licht
1
Mechanik
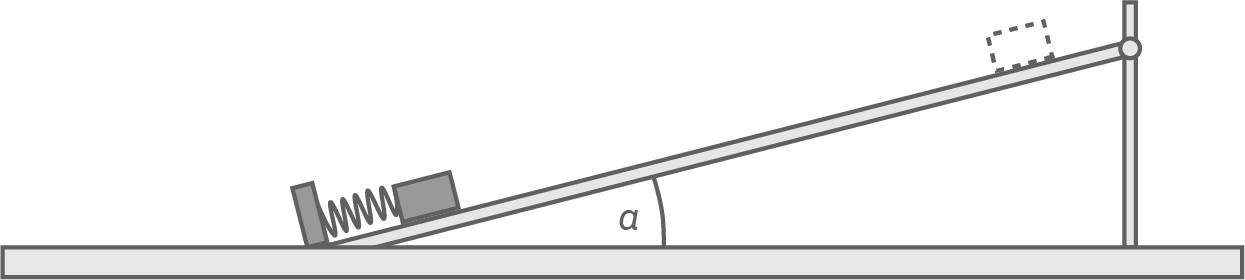
Ein Körper der Masse 
ruht auf einer geneigten Ebene vor einer gespannten Feder und berührt diese. Die Feder wird freigegeben und beschleunigt den Körper bis sich dieser im Ort 
von der Feder löst. Der Körper bewegt sich auf der geneigten Ebene aufwärts bis zum Ort 
und gleitet wieder nach unten.
Im Ort hat der Körper die potentielle Energie 
Die Reibungszahl ist für die gesamte Bewegung konstant.
Die nachfolgende nicht maßstäbliche Abbildung zeigt das Prinzip der Anordnung.
ruht auf einer geneigten Ebene vor einer gespannten Feder und berührt diese. Die Feder wird freigegeben und beschleunigt den Körper bis sich dieser im Ort von der Feder löst. Der Körper bewegt sich auf der geneigten Ebene aufwärts bis zum Ort und gleitet wieder nach unten.
Im Ort
hat der Körper die potentielle Energie
Die Reibungszahl ist für die gesamte Bewegung konstant.
Die nachfolgende nicht maßstäbliche Abbildung zeigt das Prinzip der Anordnung.
1.1
Entscheide, ob sich der Körper während seiner Bewegung aufwärts bis zum Ort gleichmäßig beschleunigt bewegt.
Begründe deine Entscheidung.
gleichmäßig beschleunigt bewegt.
Begründe deine Entscheidung.
Erreichbare BE-Anzahl: 02
1.2
Beschreibe die bei der Bewegung des Körpers vom Ort bis zum Ort ablaufenden Energieumwandlungen.
bis zum Ort ablaufenden Energieumwandlungen.
Erreichbare BE-Anzahl: 02
1.3
Am Ort hat der Körper die kinetische Energie 
.
Weise nach, dass die maximale Geschwindigkeit des Körpers 
beträgt.
hat der Körper die kinetische Energie .
Weise nach, dass die maximale Geschwindigkeit des Körpers beträgt.
Erreichbare BE-Anzahl: 02
1.4
Der Neigungswinkel der Ebene beträgt 
. Der Körper bewegt sich vom Ort bis zum Ort und legt dabei den Weg 
zurück.
Weise nach, dass die bei der Aufwärtsbewegung verrichtete Reibungsarbeit den Betrag 
hat.
. Der Körper bewegt sich vom Ort bis zum Ort und legt dabei den Weg zurück.
Weise nach, dass die bei der Aufwärtsbewegung verrichtete Reibungsarbeit den Betrag hat.
Erreichbare BE-Anzahl: 03
1.5
Der Körper gleitet vom Ort gleichmäßig beschleunigt abwärts. Die konstante Reibungszahl für die Bewegung beträgt 
.
Berechne die Beschleunigung.
gleichmäßig beschleunigt abwärts. Die konstante Reibungszahl für die Bewegung beträgt .
Berechne die Beschleunigung.
Erreichbare BE-Anzahl: 03
2
Äußerer lichtelektrischer Effekt
Monochromatisches Licht trifft auf die lichtempfindliche Schicht einer Vakuumfotozelle. Die kinetische Energie der Fotoelektronen wird mit der Gegenfeldmethode ermittelt.
2.1
Beschreibe das Prinzip eines Experiments, mit dem die kinetische Energie der schnellsten Fotoelektronen ermittelt werden kann.
Erreichbare BE-Anzahl: 03
2.2
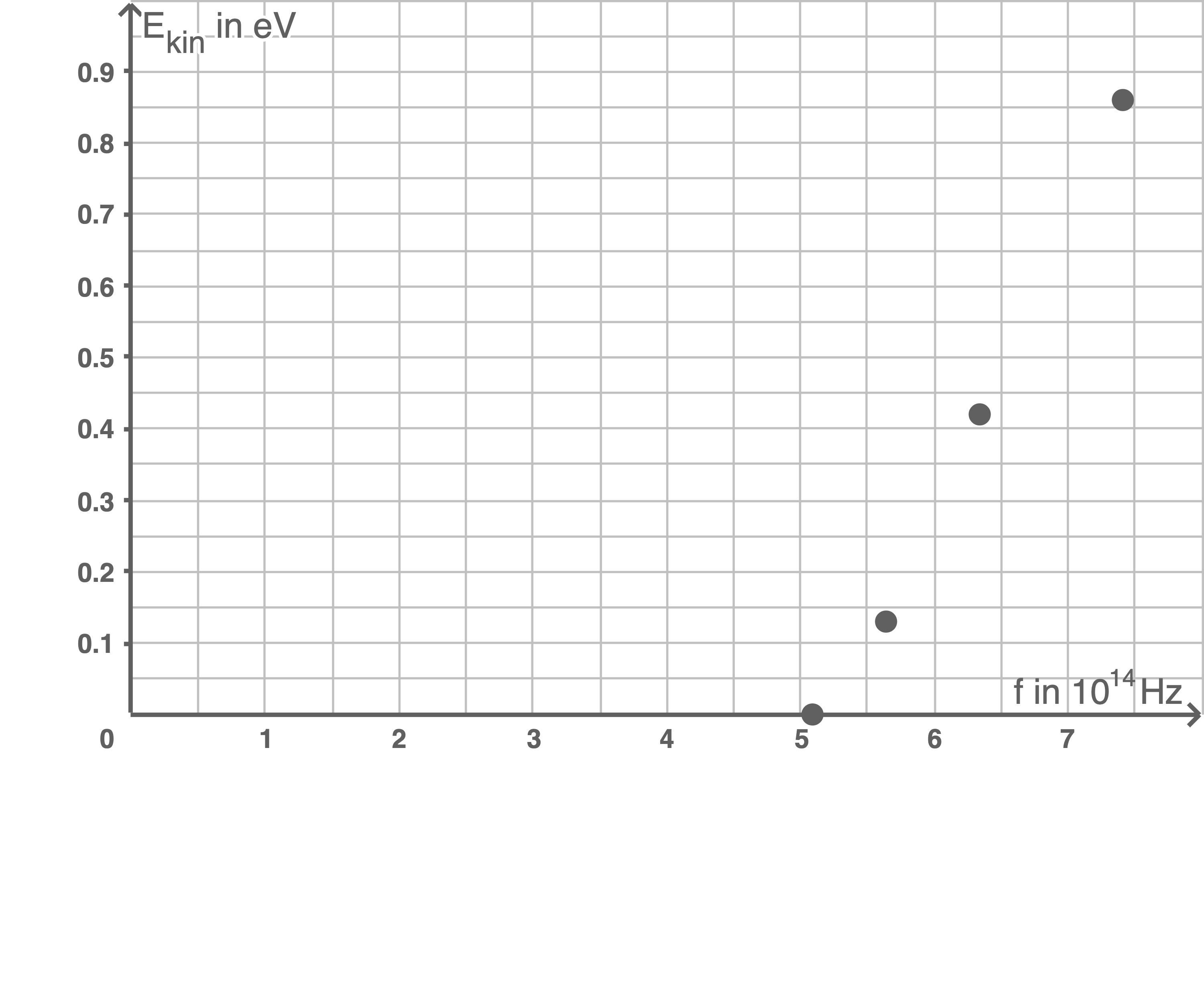
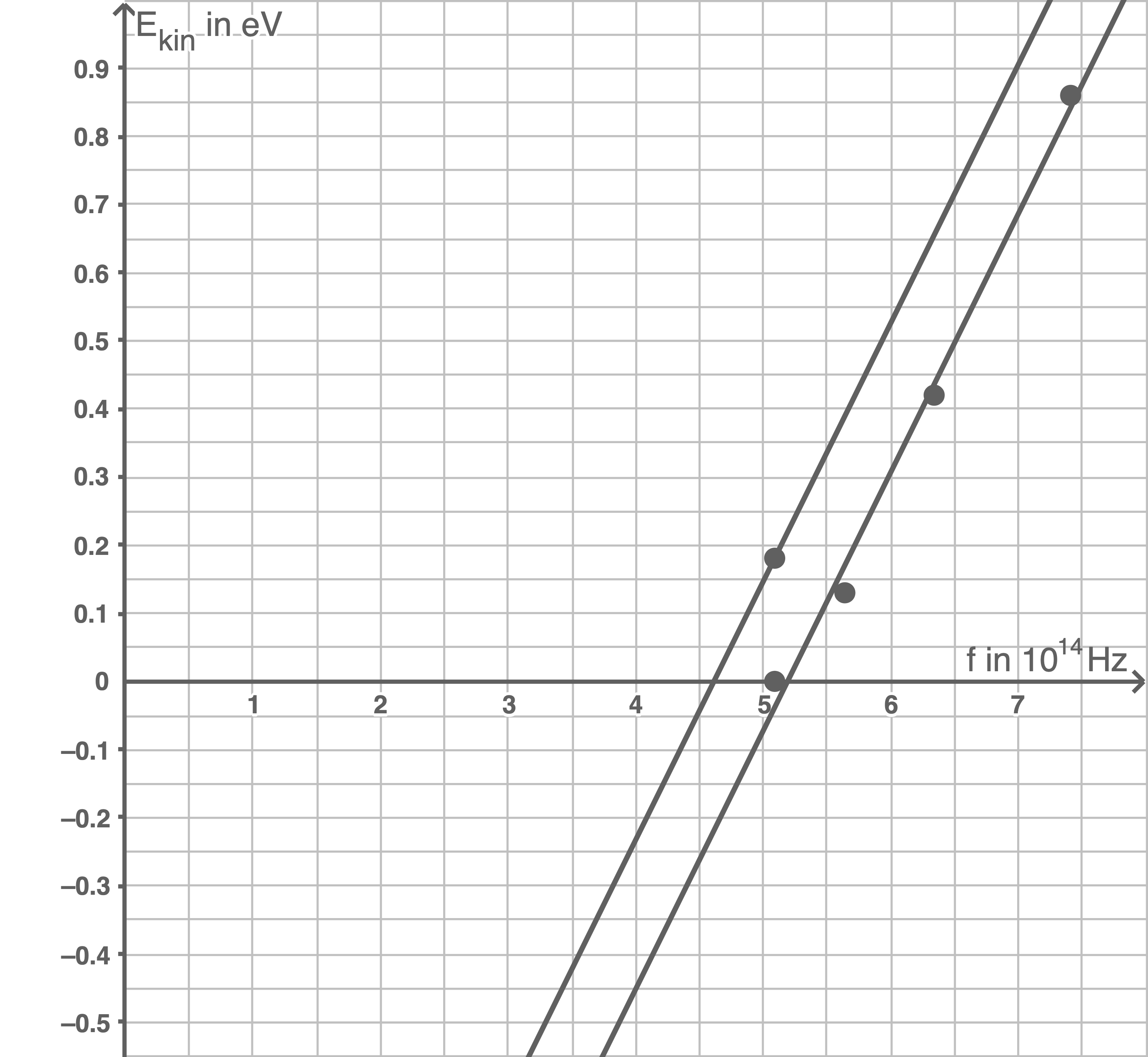
Die Gegenspannung 
wird für unterschiedliche Frequenzen gemessen.
wird für unterschiedliche Frequenzen gemessen.
| Farbe |  in  Hz |
 in V |
|---|---|---|
| gelb | 5,09 | - |
| grün | 5,64 | 0,13 |
| blau | 6,34 | 0,42 |
| violett | 7,41 | 0,86 |
2.2.1
Zeichne das zugehörige 
-Diagramm.
-Diagramm.
Erreichbare BE-Anzahl: 02
2.2.2
Gib die Grenzfrequenz an.
Erreichbare BE-Anzahl: 01
2.2.3
Ermittle unter Nutzung aller relevanten Messwerte das Planck'sche Wirkungsquantum.
Erreichbare BE-Anzahl: 02
2.3
Gelbes Licht löst keine Elektronen heraus.
Begründe unter Nutzung von Einsteins Lichtquantenhypothese diesen Sachverhalt.
Erreichbare BE-Anzahl: 03
2.4
Das Experiment wird mit einer anderen Vakuumfotozelle wiederholt.
Bei dieser löst gelbes Licht Elektronen heraus.
Trage für diese Vakuumfotozelle einen möglichen Graphen in das Diagramm aus Teilaufgabe 2.2.1 ein.
Erreichbare BE-Anzahl: 02
3
Die Lichtbrechung an einem flachen quaderförmigen Glaskörper wird experimentell untersucht.
Unter Nutzung einfarbigen Lichts sollen die Brechzahl für die Glassorte und die zugehörige Lichtgeschwindigkeit ermittelt werden.
Erläutere die Durchführung und die Auswertung eines möglichen Experiments.
Erreichbare BE-Anzahl: 05
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Auf den Körper wirkt die Federkraft, die Hangabtriebskraft und die Reibung 
Die Hangabtreibskraft und die Reibung ist zeitlich konstant. Damit folgt für die Beschleunigung 
des Körpers:
Die Beschleunigung ist abhängig von dem Ort 
an dem sich der Körper befindet. Da sich der Ort 
des Körpers mit der Zeit verändert und dementsprechend nicht konstant ist, kann auch die Beschleunigung nicht konstant sein. Es handelt sich folglich nicht um eine gleichmäßige Beschleunigung.
Die Hangabtreibskraft und die Reibung ist zeitlich konstant. Damit folgt für die Beschleunigung des Körpers:
Die Beschleunigung 
![\(\begin{array}[t]{rll}
F_{\text{ges}}&=& k\cdot x -m\cdot g\cdot \sin\left( \alpha\right)-F_{R} &\quad \scriptsize \\[5pt]
m\cdot a&=& k\cdot x -m\cdot g\cdot \sin\left( \alpha\right)-F_{R} &\quad \scriptsize \mid\; \cdot \dfrac{1}{m} \\[5pt]
a&=& \dfrac{k}{m}\cdot x -g\cdot \sin\left( \alpha\right)-\dfrac{F_{R}}{m} &\quad \scriptsize \mid\; -g\cdot \sin\left( \alpha\right)-\dfrac{F_{R}}{m} =\text{konst}=C_1\\[5pt]
a&=& \dfrac{k}{m}\cdot x +C_1&\quad \scriptsize \mid\;\dfrac{k}{m}=\text{konst}=C_2 \\[5pt]
a&=& C_2\cdot x +C_1
\end{array}\)](https://www.schullv.de/resources/formulas/fa6db49fdd15912d614435e82b8f665cf82e00f0775b3610adf2d1ddd4f09f37_light.svg)
ist abhängig von dem Ort an dem sich der Körper befindet. Da sich der Ort des Körpers mit der Zeit verändert und dementsprechend nicht konstant ist, kann auch die Beschleunigung nicht konstant sein. Es handelt sich folglich nicht um eine gleichmäßige Beschleunigung.
1.2
Am Ort O hat der Körper kinetische Energie, welche bei seiner Aufwärtsbewegung zum Ort P in potentielle Energie, Lageenergie, umgewandelt wird. Am Umkehrpunkt P hat der Körper keine Geschwindigkeit und damit auch keine kinetische Energie mehr, sondern besitzt ausschließlich potentielle Energie. Aufgrund der Reibung wird ein Teil der kinetischen Energie nicht in potentielle Energie umgewandelt, sondern in Wärmeenergie.
1.3
![\(\begin{array}[t]{rll}
E_{\text{kin,O}} &=&\dfrac{1}{2}\cdot m\cdot v^2&\quad \scriptsize \mid\;\cdot 2 \\[5pt]
2\cdot E_{\text{kin,O}}&=& m\cdot v^2 &\quad \scriptsize \mid\; \cdot \dfrac{1}{m} \\[5pt]
\dfrac{2\cdot E_{\text{kin,O}}}{m} &=& v^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{2\cdot E_{\text{kin,O}}}{m}} &=& v
\end{array}\)](https://www.schullv.de/resources/formulas/07d7872b99ea3aaf84f5ceccd65171e0f5282f52b454db731c2cdc315f37209a_light.svg)
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v&=&\sqrt{2\cdot\dfrac{E_{\text{kin,O}}}{m}} &\quad \scriptsize \\[5pt]
&=& \sqrt{2\cdot\dfrac{0,13\;\text{J}}{80,0 \;\text{g}}}&\quad \scriptsize \\[5pt]
&=& \sqrt{2\cdot\dfrac{0,13\;\text{J}}{0,08 \;\text{kg}}}&\quad \scriptsize \\[5pt]
&=& 1,80 \;\dfrac{\text{m}}{\text{s}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/3994921cdc479cc85f91516468efc030d497748ca3f8bd8f32a9b6f9bd6f06c4_light.svg)
1.4
Die Energieerhaltung liefert:
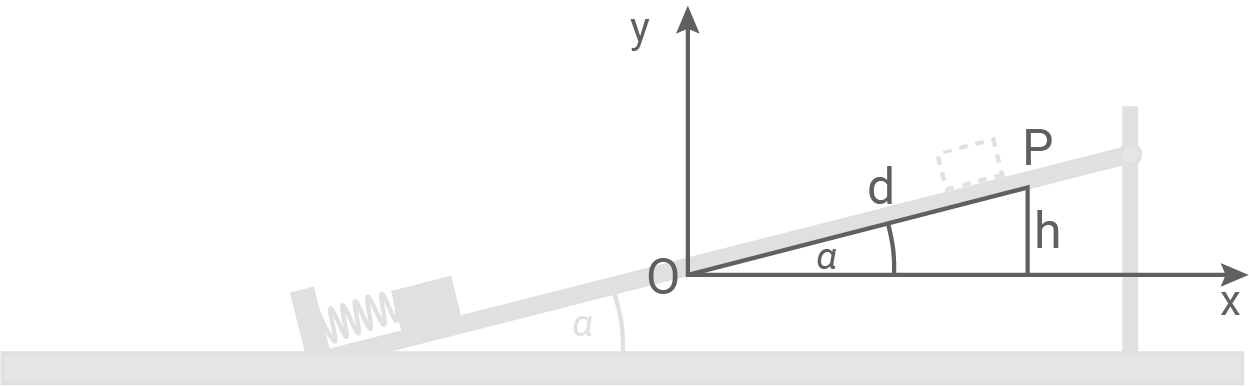Die Höhe 
die der Körper zwischen O und P erreicht, ergibt sich aus der Sinus-Beziehung im rechtwinkligen Dreieck:
![\(\begin{array}[t]{rll}
\sin\left(\alpha\right)&=& \dfrac{h}{d} &\quad \scriptsize \mid\; \cdot d\\[5pt]
\sin\left(\alpha\right)\cdot d&=& h
\end{array}\)](https://www.schullv.de/resources/formulas/be69d900be2f7d5c78d21f0475126d22583d58e6850ee02d724b03474f97976a_light.svg)
Einsetzen in die Beziehung für die Reibungsarbeit liefert:
![\(\begin{array}[t]{rll}
W_{\text{Reibung,P}} &=& E_{\text{kin,O}}-m\cdot g\cdot h&\quad \scriptsize \\[5pt]
&=& E_{\text{kin,O}}-m\cdot g\cdot \sin\left(\alpha\right)\cdot d
\end{array}\)](https://www.schullv.de/resources/formulas/b3355a648cfa93e31874d2d85cc7113665a16e2170186cb42da2976645a26e15_light.svg)
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
E_{\text{kin,O}} &=& E_{\text{pot,P}}+W_{\text{Reibung,P}}&\quad \scriptsize \mid\;-E_{\text{pot,P}} \\[5pt]
E_{\text{kin,O}}-E_{\text{pot,P}} &=& W_{\text{Reibung,P}}&\quad \scriptsize \\[5pt]
W_{\text{Reibung,P}} &=& E_{\text{kin,O}}-E_{\text{pot,P}}&\quad \scriptsize \\[5pt]
W_{\text{Reibung,P}} &=& E_{\text{kin,O}}-m\cdot g\cdot h
\end{array}\)](https://www.schullv.de/resources/formulas/f1b0e9a416c63dc16bd4aafc3056030642eb6088e5f1df0021999ef7dc0e9e47_light.svg)
die der Körper zwischen O und P erreicht, ergibt sich aus der Sinus-Beziehung im rechtwinkligen Dreieck:
Einsetzen in die Beziehung für die Reibungsarbeit liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
W_{\text{Reibung,P}}&=& E_{\text{kin,O}}-m\cdot g\cdot \sin\left(\alpha\right)\cdot d &\quad \scriptsize \\[5pt]
&=& 0,13 \;\text{J}-80 \;\text{g} \cdot 9,81\;\dfrac{\text{m}}{\text{s}^2}\cdot \sin\left(10°\right)\cdot 0,575 \;\text{m} &\quad \scriptsize \\[5pt]
&=& 0,13 \;\text{J}-0,08 \;\text{kg} \cdot 9,81\;\dfrac{\text{m}}{\text{s}^2}\cdot \sin\left(10°\right)\cdot 0,575 \;\text{m} &\quad \scriptsize \\[5pt]
&=& 0,052 \;\text{J}
\end{array}\)](https://www.schullv.de/resources/formulas/3e0a6cbb2ad8e1712f3249393d4d20c4c55ba9421c354542a006dc7ba5acfda0_light.svg)
1.5
Die resultierende beschleunigte Kraft 
entspricht der Differenz von der Hangabtriebskraft 
und von der Reibungskraft 
:
Einsetzen der Werte liefert:
entspricht der Differenz von der Hangabtriebskraft und von der Reibungskraft :
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
F_B&=& F_H-F_R &\quad \scriptsize \\[5pt]
m\cdot a&=& m\cdot g\cdot \sin\left(\alpha\right)- \mu\cdot m\cdot g\cdot \cos\left(\alpha\right) &\quad \scriptsize \mid\;\cdot \dfrac{1}{m} \\[5pt]
a&=& g\cdot \sin\left(\alpha\right)- \mu \cdot g\cdot \cos\left(\alpha\right) &\quad \scriptsize \\[5pt]
a &=& g \cdot \left(\sin\left(\alpha\right)- \mu \cdot \cos\left(\alpha\right)\right)
\end{array}\)](https://www.schullv.de/resources/formulas/b70acd59fe002ed0e9c63b238ca3f7156add6dccb36b0ac4295ff41b235d6bd6_light.svg)
![\(\begin{array}[t]{rll}
a &=& g \cdot \left(\sin\left(\alpha\right)- \mu \cdot \cos\left(\alpha\right)\right) &\quad \scriptsize \\[5pt]
&=& 9,81 \; \dfrac{\text{m}}{\text{s}^2} \cdot \left(\sin\left(10°\right)- 0,12 \cdot \cos\left(10°\right)\right) &\quad \scriptsize \\[5pt]
&=& 0.54 \; \dfrac{\text{m}}{\text{s}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/17c48593621c6932f191ecd2a63b95e644d6d53b09b20fb2c14b68e7a8d8e554_light.svg)
2.1
Bei der Gegenfeldmethode in einem Experiment zur Bestimmung der kinetischen Energie der schnellsten Fotoelektronen wird eine variable Gegenspannung zwischen zwei Elektroden einer Vakuumfotozelle angelegt. Die Spannung wird schrittweise erhöht, bis kein Elektronenstrom mehr gemessen wird. Durch weitere Erhöhung der Spannung werden nur die schnellsten Elektronen gestoppt, während langsamere Elektronen weiterhin einen messbaren Strom erzeugen. Die Spannung, bei der der Strom umkehrt, gibt die kinetische Energie der schnellsten Elektronen an. Durch Messungen bei verschiedenen Lichtfrequenzen können Zusammenhänge zwischen Lichtenergie und kinetischer Energie erforscht werden.
2.2.1
Für die kinetische Energie 
gilt:
![\(\begin{array}[t]{rll}
E_{\text{kin,f}}&=& e\cdot U_{\text{f}} &\quad \scriptsize \mid\; e=1,602176634 \cdot 10^{-19} \;\text{C} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/24f43c513bb34fa87079f17519c7a62d9068c217a7b3bc8dc420ad97acf13641_light.svg)
gilt:
| Farbe | in  |
in  |
 in  |
|---|---|---|---|
| gelb | 5,09 | - | - |
| grün | 5,64 | 0,13 | 0,13 |
| blau | 6,34 | 0,42 | 0,42 |
| violett | 7,41 | 0,86 | 0,86 |
2.2.2
Die Gegenfrequenz ist die Frequenz, bei der keine Elektronen die Kathode erreichen und somit die kinetische Energie gleich Null ist. Es kann hier also keine Spannung gemessen werden. Das entspricht der Frequenz in der Tabelle bei Gelb mit der Spannung 0 und somit einer kinetischen Energie von 0 . Die Gegenfrequenz beträgt folglich 
.
gemessen werden. Das entspricht der Frequenz in der Tabelle bei Gelb mit der Spannung 0 und somit einer kinetischen Energie von 0 . Die Gegenfrequenz beträgt folglich .
2.2.3
und der kinetischen Energie 
zu erkennen. Die Regressionsgerade durch die eingezeichneten Punkte entspricht der Einstein-Gleichung:
Das Planck'sche Wirkungsquantum entspricht hierbei der Steigung. Diese kann mit Hilfe der Abbildung bestimmt werden.
Dazu werden die Koordinaten zweier beliebiger Punkte abgelesen.
Zum Beispiel: 
und 
Steigung der Regressionsgeraden
Somit folgt:
![\(\begin{array}[t]{rll}
h&=& 0,42 \;\dfrac{\text{eV}}{10^{14}\text{Hz}}\\[5pt]
&=&0,42 \;\dfrac{1,602\cdot 10^{-19}\;\text{J}}{10^{14}\text{Hz}}\\[5pt]
&\approx& 6,73 \cdot 10^{-34}\;\text{Js}
\end{array}\)](https://www.schullv.de/resources/formulas/21f4ab57e446ade779d2c3154a5e73392d258ea5027a526a8377ed057ed0d17a_light.svg)
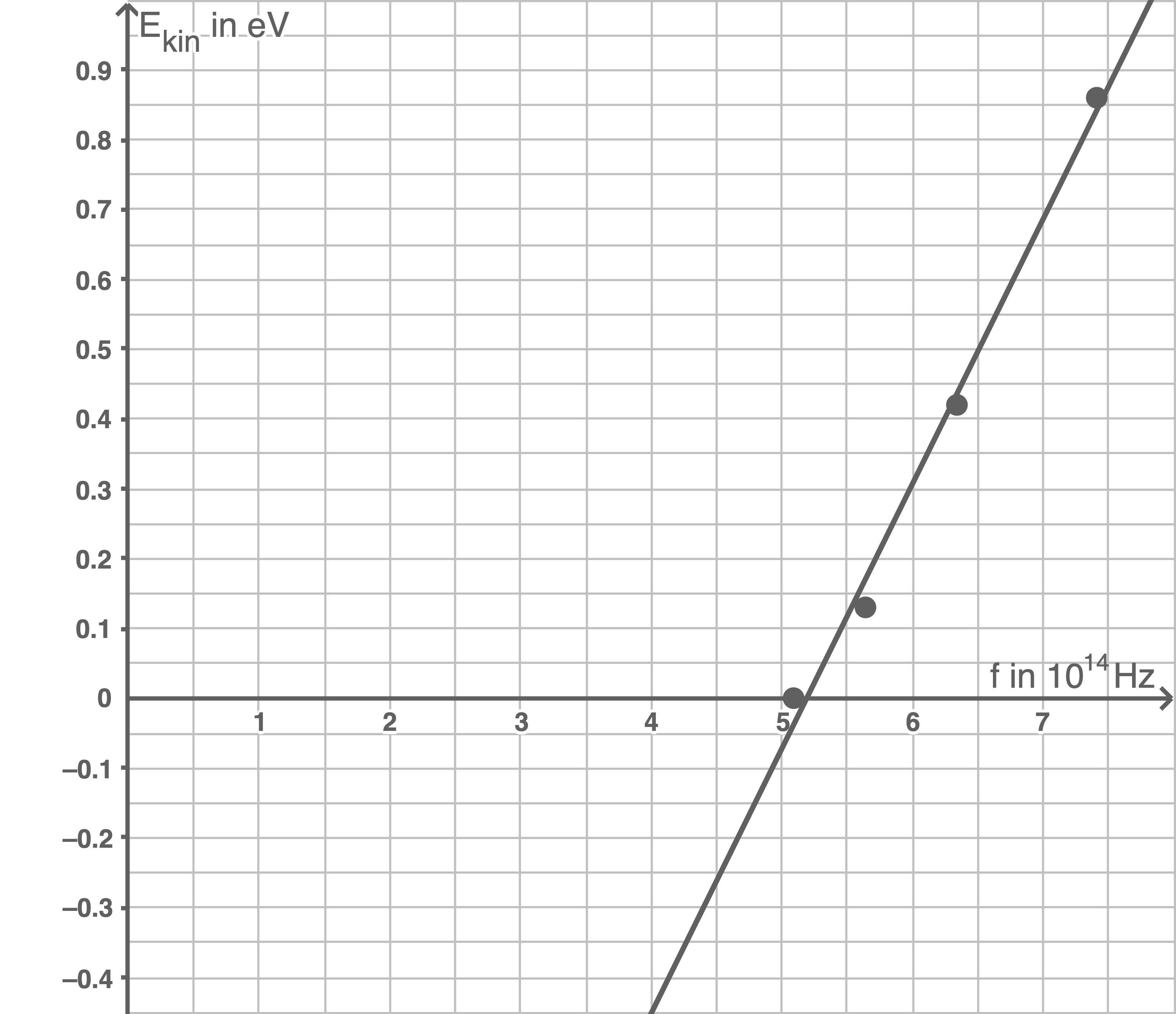
2.3
Gelbes Licht löst keine Elektronen aus, da seine Photonen nicht genug Energie haben, um die Austrittsarbeit der Elektronen in der lichtempfindlichen Schicht zu überwinden. Dies ist gemäß Einsteins Lichtquantenhypothese 
, da die Energie eines Photons direkt proportional zur Frequenz des Lichts ist. Das gelbe Licht hat eine niedrigere Frequenz und somit eine geringere Energie pro Photon im Vergleich zu Licht höherer Frequenzen (wie blau oder violett), wodurch kein äußerer lichtelektrischer Effekt auftritt.
, da die Energie eines Photons direkt proportional zur Frequenz des Lichts ist. Das gelbe Licht hat eine niedrigere Frequenz und somit eine geringere Energie pro Photon im Vergleich zu Licht höherer Frequenzen (wie blau oder violett), wodurch kein äußerer lichtelektrischer Effekt auftritt.
2.4
Da gelbes Licht nun Elektronen auslösen kann, wird für gelbes Licht ein Wert für die Gegenspannung existieren, der größer als Null ist.
3.
Ein flacher quaderförmiger Glaskörper wird stabil auf eine Tischkante platziert. Eine Lichtquelle wird so eingestellt, dass sie einfarbiges Licht auf den Glaskörper strahlt. Die Lichtstrahlen treffen in einem bestimmten Winkel auf die Glasoberfläche. Dabei werden der Einfallswinkel 
(Winkel zwischen dem einfallenden Lichtstrahl und der senkrechten Linie zur Glasoberfläche) und der Brechungswinkel 
(Winkel zwischen dem gebrochenen Lichtstrahl und der senkrechten Linie zur Glasoberfläche) gemessen und notiert. Der Versuch wird anschließend mit anderen einfarbigen Lichtern wiederholt, wobei die entsprechenden Einfallswinkel und Brechungswinkel gemessen und notiert werden. Um ein genaueres Messergebnis zu erhalten, sollte der Versuch mit jeder Lichtquelle mehrmals durchgeführt werden, damit der Durchschnitt der gemessenen Einfallswinkel und Brechnungswinkel gebildet werden kann. Die Brechzahl 
wird über das Snell'sche Gesetz berechnet:
![\(\begin{array}[t]{rll}
n = \dfrac{\sin(\alpha)}{\sin(\beta)}
\end{array}\)](https://www.schullv.de/resources/formulas/3ba02a2e97fe5a976b7ff41c90d721d75a32e31bef1e14de0d2e3af829e92001_light.svg)
Für jede Lichtquelle wird das arithmetische Mittel für den Einfallswinkel und das arithmetische Mittel des Brechungswinkels in das Snell'sche Brechungsgesetz eingesetzt. Anschließend werden die errechneten Brechzahlen aufsummiert und durch die Anzahl der Messungen geteilt. Das Ergebnis ist die ermittelte Brechzahl des Glaskörpers. Für die Lichtgeschwindigkeit 
im Glaskörper gilt:
![\(\begin{array}[t]{rll}
v = \dfrac{c}{n}
\end{array}\)](https://www.schullv.de/resources/formulas/e2a74c8ea3450d28e62aaab0fb1b3d2e81e1a4a784fb109984342370ed2b785d_light.svg)
Wobei 
der Lichtgeschwindigkeit im Vakuum entspricht und die gemessene Brechzahl darstellt.
(Winkel zwischen dem einfallenden Lichtstrahl und der senkrechten Linie zur Glasoberfläche) und der Brechungswinkel (Winkel zwischen dem gebrochenen Lichtstrahl und der senkrechten Linie zur Glasoberfläche) gemessen und notiert. Der Versuch wird anschließend mit anderen einfarbigen Lichtern wiederholt, wobei die entsprechenden Einfallswinkel und Brechungswinkel gemessen und notiert werden. Um ein genaueres Messergebnis zu erhalten, sollte der Versuch mit jeder Lichtquelle mehrmals durchgeführt werden, damit der Durchschnitt der gemessenen Einfallswinkel und Brechnungswinkel gebildet werden kann. Die Brechzahl wird über das Snell'sche Gesetz berechnet:
Für jede Lichtquelle wird das arithmetische Mittel für den Einfallswinkel und das arithmetische Mittel des Brechungswinkels in das Snell'sche Brechungsgesetz eingesetzt. Anschließend werden die errechneten Brechzahlen aufsummiert und durch die Anzahl der Messungen geteilt. Das Ergebnis ist die ermittelte Brechzahl des Glaskörpers. Für die Lichtgeschwindigkeit im Glaskörper gilt:
Wobei der Lichtgeschwindigkeit im Vakuum entspricht und die gemessene Brechzahl darstellt.