Teil B – Bewegungen, Elektronen
1
Eine Standardsituation beim Fußball ist der Einwurf von der Seitenauslinie. Dabei wird der Ball mit beiden Händen über den Kopf in das Spielfeld geworfen.
Dieser Vorgang wird modellhaft als schräger Wurf vereinfacht.
Für die Wurfbahn gilt die Gleichung 
1.1
Erläutere das Superpositionsprinzip am Beispiel des schrägen Wurfs.
Erreichbare BE-Anzahl: 02
1.2
Ein Fußballer übt den Einwurf.
Der Abwurfwinkel beträgt , die Abwurfhöhe
, die Abwurfhöhe 
Der Abwurfwinkel beträgt
1.2.1
Die Wurfweite (horizontal) beträgt 
Ermittle die Geschwindigkeit, mit der der Ball abgeworfen wurde.
Ermittle die Geschwindigkeit, mit der der Ball abgeworfen wurde.
Erreichbare BE-Anzahl: 02
1.2.2
Der Fußballer wirft den Ball mit der Abwurfgeschwindigkeit  .
.
In diesem Moment läuft ein Mitspieler geradlinig mit konstanter Geschwindigkeit genau in Richtung des Werfers, er ist zum Zeitpunkt des Abwurfes von ihm entfernt.
von ihm entfernt.
Der Ball trifft den Mitspieler in der Höhe auf dessen Brust.
auf dessen Brust.
Ermittle für diesen Zeitpunkt die Entfernung von Werfer und Mitspieler sowie die Geschwindigkeit des Mitspielers.
In diesem Moment läuft ein Mitspieler geradlinig mit konstanter Geschwindigkeit genau in Richtung des Werfers, er ist zum Zeitpunkt des Abwurfes
Der Ball trifft den Mitspieler in der Höhe
Ermittle für diesen Zeitpunkt die Entfernung von Werfer und Mitspieler sowie die Geschwindigkeit des Mitspielers.
Erreichbare BE-Anzahl: 05
2
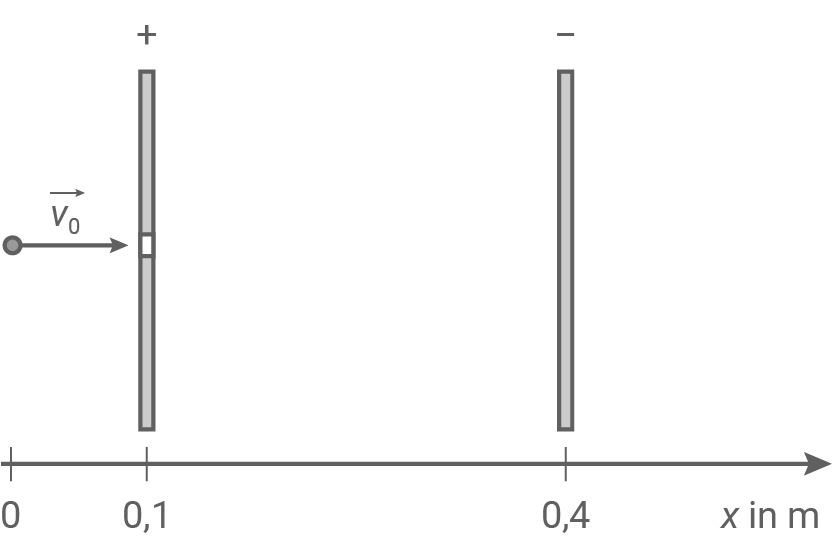
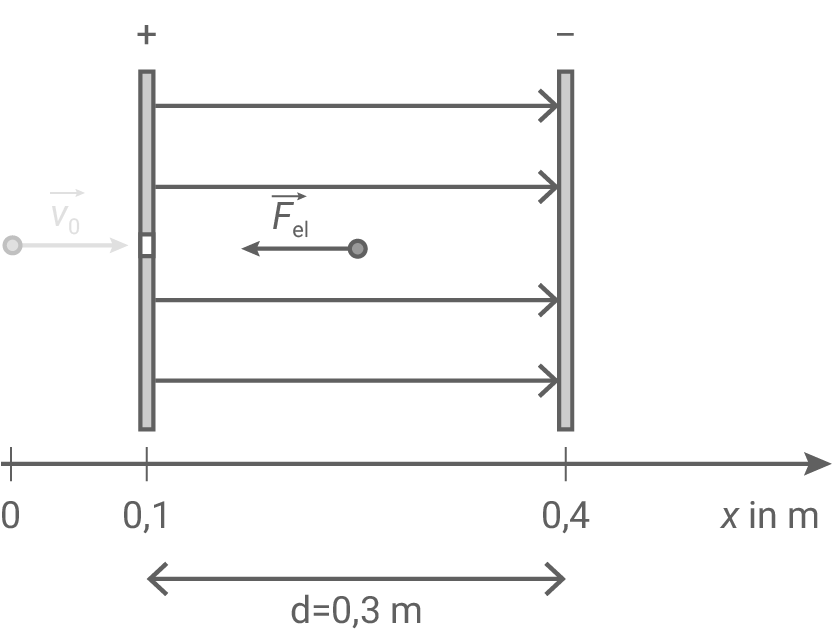
Ein Elektron tritt durch eine Öffnung in der positiv geladenen Platte eines Plattenkondensators parallel zu den Feldlinien in das homogene Feld eines auf die Spannung  geladenen Plattenkondensators ein.
Hinweis: Vereinfacht wird angenommen, dass das Feld ausschließlich im Innenraum des Kondensators existiert.
Die Abbildung 1 zeigt das Prinzip.
geladenen Plattenkondensators ein.
Hinweis: Vereinfacht wird angenommen, dass das Feld ausschließlich im Innenraum des Kondensators existiert.
Die Abbildung 1 zeigt das Prinzip.
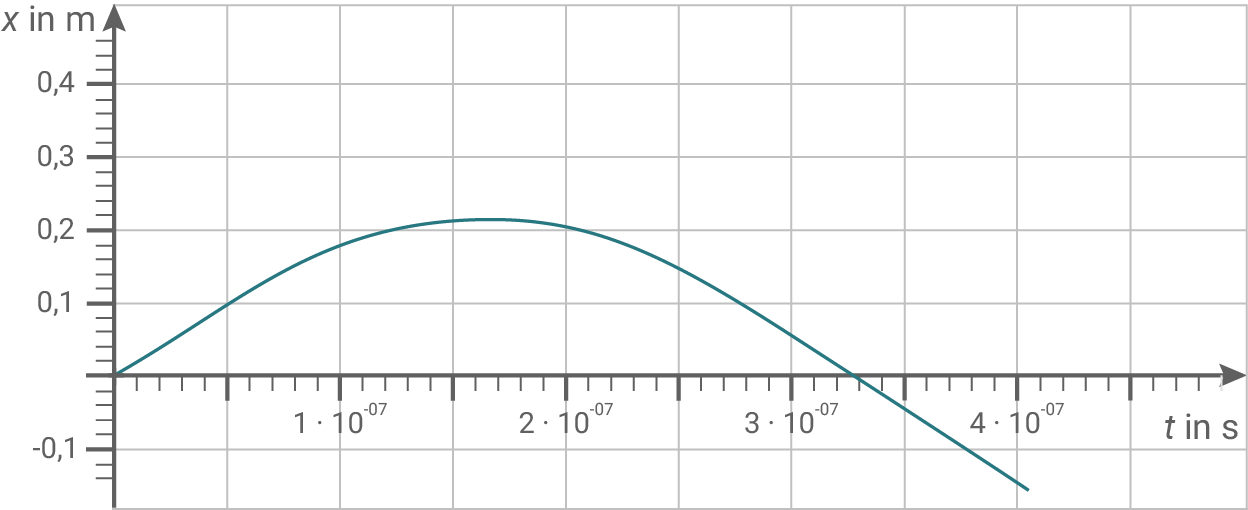
 Die Abbildung 2 zeigt das
Die Abbildung 2 zeigt das  -Diagramm für die Bewegung des Elektrons.
-Diagramm für die Bewegung des Elektrons.


2.1
Weise nach, dass die Geschwindigkeit, mit der das Elektron in das Feld eintritt,  beträgt.
beträgt.
Erreichbare BE-Anzahl: 02
2.2
Zum Zeitpunkt  erreicht das Elektron seinen maximalen Abstand zur positiven Platte
erreicht das Elektron seinen maximalen Abstand zur positiven Platte  .
.
Gib und
und  an.
an.
Gib
Erreichbare BE-Anzahl: 02
2.3
Berechne den Betrag der Spannung, auf die der Kondensator geladen ist.
Erreichbare BE-Anzahl: 03
3
Elektronen und Photonen als Quantenobjekte
3.1
Im Folgenden wird die Anregung von Neon-Atomen durch Elektronenstöße betrachtet.
3.1.1
Ein Neon-Atom wechselwirkt mit einem freien Elektron und absorbiert die Energie  .
.
Das angeregte Neon-Atom emittiert ein Quant der Wellenlänge (Orange) und geht dadurch in einen energetischen Zwischenzustand über.
(Orange) und geht dadurch in einen energetischen Zwischenzustand über.
Berechne die Energie dieses Zustands bezüglich des Grundniveaus
Das angeregte Neon-Atom emittiert ein Quant der Wellenlänge
Berechne die Energie dieses Zustands bezüglich des Grundniveaus
Erreichbare BE-Anzahl: 03
3.1.2
Elektronen durchlaufen aus der Ruhe heraus die Spannung  in einer mit Neongas gefüllten Röhre. Es werden zwei schmale orangefarbig leuchtende Bereiche beobachtet.
in einer mit Neongas gefüllten Röhre. Es werden zwei schmale orangefarbig leuchtende Bereiche beobachtet.
Erkläre diese Beobachtung.
Erkläre diese Beobachtung.
Erreichbare BE-Anzahl: 02
3.2
Ein Energieniveau des Neons ist metastabil und geeignet, um Laserlicht zu erzeugen.
Erläutere das physikalische Prinzip der Entstehung von Laserstrahlung.
Erläutere das physikalische Prinzip der Entstehung von Laserstrahlung.
Erreichbare BE-Anzahl: 03
3.3
Elektronenbeugung
3.3.1
Erläutere ein Experiment zum Nachweis der Elektronenbeugung.
Erreichbare BE-Anzahl: 03
3.3.2
Elektronen bewegen sich mit der Geschwindigkeit  .
.
Berechne den Impuls und die Wellenlänge eines Elektrons.
Berechne den Impuls und die Wellenlänge eines Elektrons.
Erreichbare BE-Anzahl: 03
1.1
Superpositionsprinzip (Prinzip der ungestörten Überlagerung)
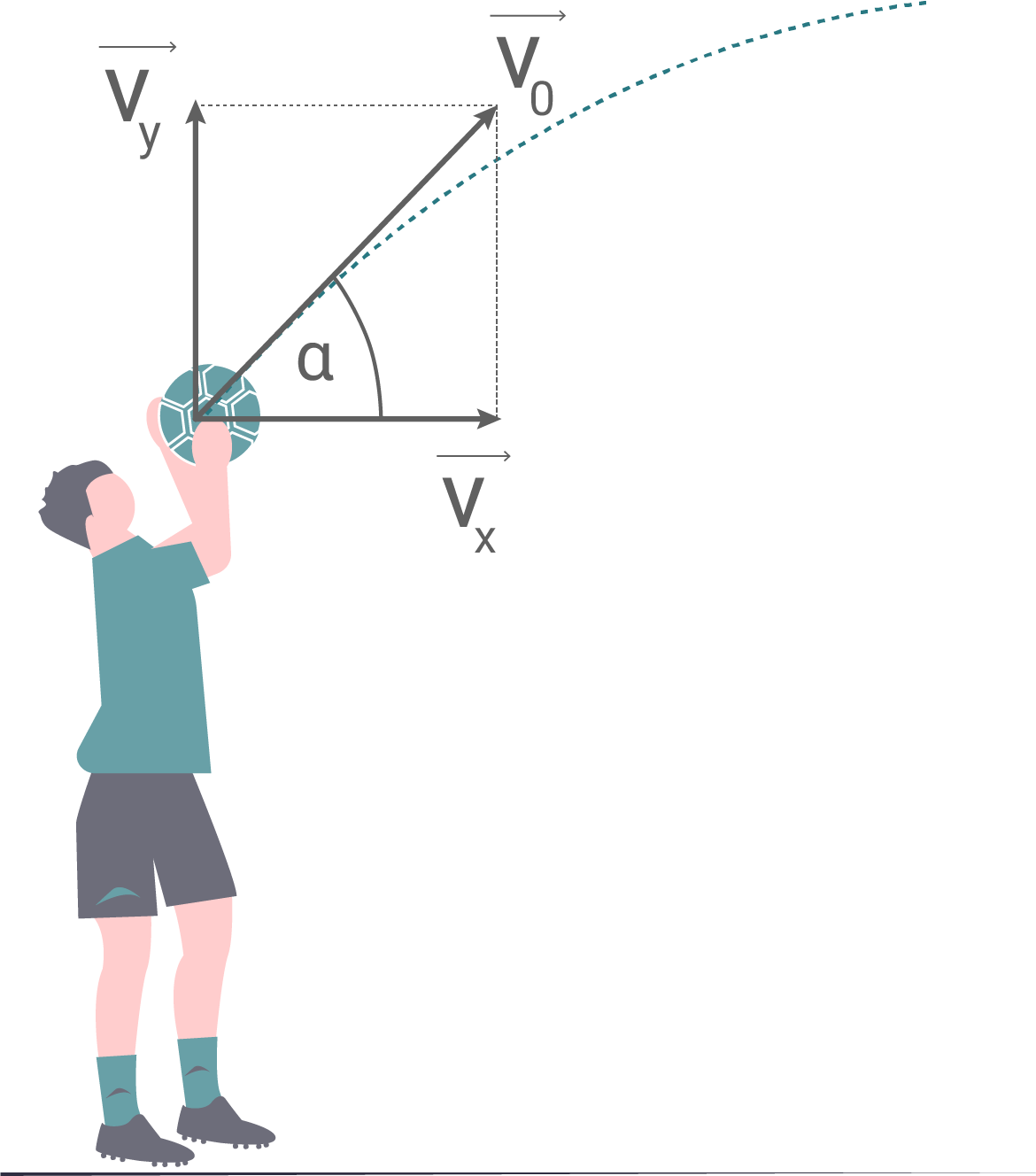 Die Bewegungen in horizontale, als auch vertikale Richtung erfolgen unabhängig voneinander.
Durch die Überlagerung (Superposition) ergibt sich die Gesamtbewegung.
Die Bewegungen in horizontale, als auch vertikale Richtung erfolgen unabhängig voneinander.
Durch die Überlagerung (Superposition) ergibt sich die Gesamtbewegung.
- Gesamtbewegung, die aus der Überlagerung voneinander unabhängigen Teilbewegungen stattfindet
- ungestörte Überlagerung bedeutet: Reibungskräfte wie beispielsweise der Luftwiderstand werden vernachlässigt
Teilbewegungen des schrägen (Ein-)Wurfes
Bewegung in horizontale  -Richtung:
-Richtung:
 -Richtung:
-Richtung:
- Ball bewegt sich gleichförmig mit konstanter Geschwindigkeit
- Geschwindigkeit entspricht horizontaler Komponente
der Anfangsgeschwindigkeit
- Ball bewegt sich gleichmäßig beschleunigt nach oben (wie bei einem senkrechten Wurf)
- Startgeschwindigkeit entspricht vertikaler Komponente
der Anfangsgeschwindigkeit
- Beschleunigung:
(wie beim freien Fall)

1.2.1
Gegeben: 

 Gesucht:
Gesucht:  Lösung: Da der Ball auf dem Boden aufkommt, folgt
Lösung: Da der Ball auf dem Boden aufkommt, folgt  Die Fallbeschleunigung ist mit
Die Fallbeschleunigung ist mit  gegeben.
Alle gegebenen Werte werden in die Gleichung der Wurfbahn eingesetzt und diese mit dem solve-Befehl des Taschenrechners nach
gegeben.
Alle gegebenen Werte werden in die Gleichung der Wurfbahn eingesetzt und diese mit dem solve-Befehl des Taschenrechners nach  gelöst:
gelöst:
1.2.2
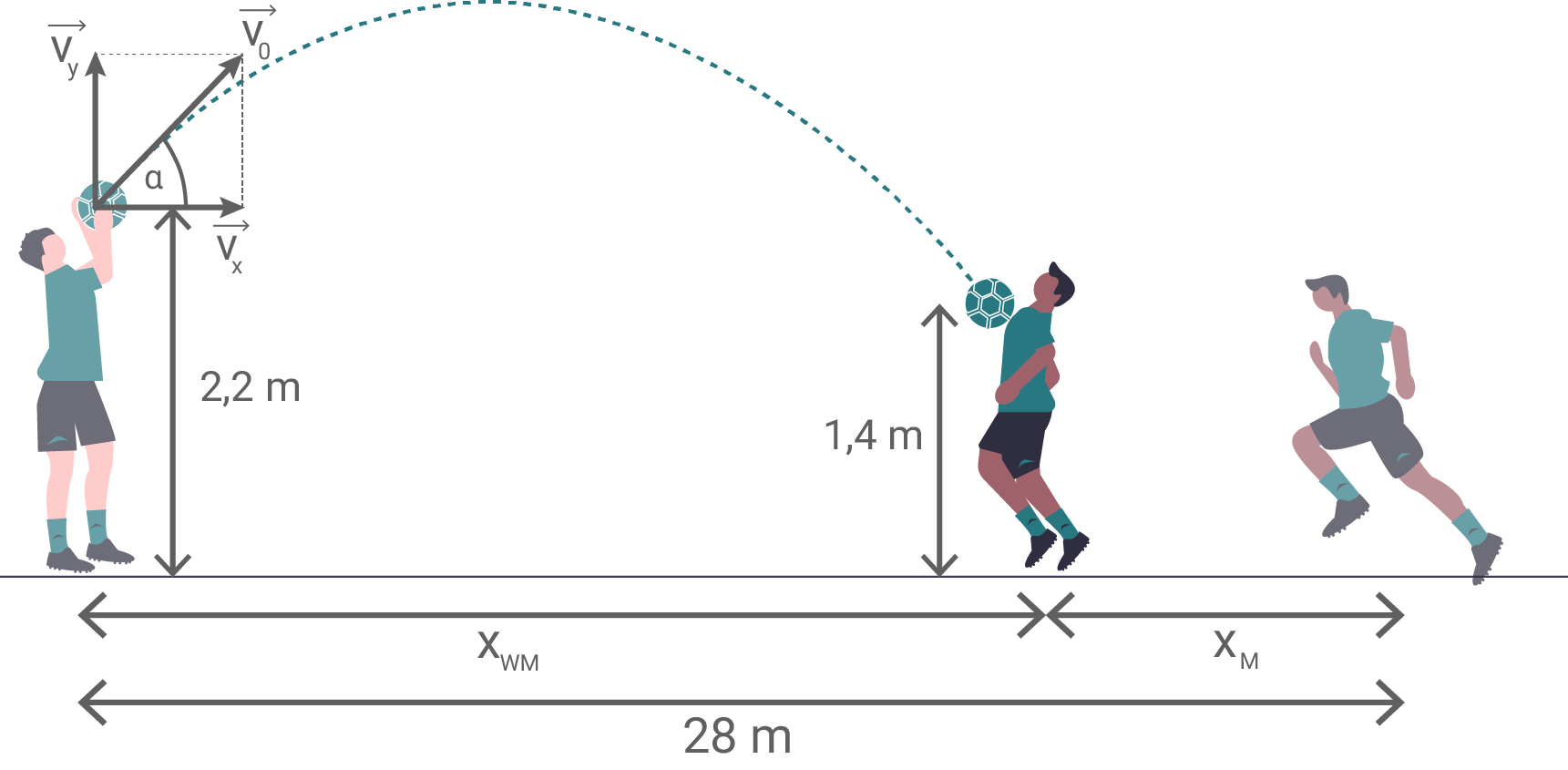
Hilfsskizze (nicht maßstäblich)
Entfernung von Werfer und Mitspieler ermitteln
Gegeben:Geschwindigkeit des Mitspielers ermitteln
Gegeben: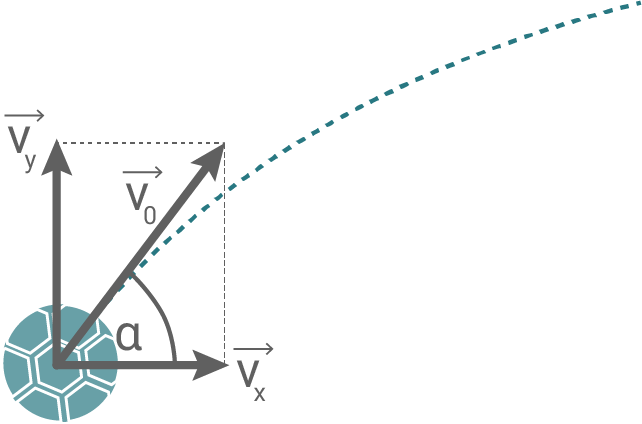
2.1
Vorüberlegungen aus dem Sachzusammenhang
(Zum Lösen der Aufgabe reicht der Rechenweg) Aus Abbildung 1 folgt: Das Elektron tritt bei in das homogene Feld des Plattenkondensators ein.
in das homogene Feld des Plattenkondensators ein.



(Zum Lösen der Aufgabe reicht der Rechenweg) Aus Abbildung 1 folgt: Das Elektron tritt bei
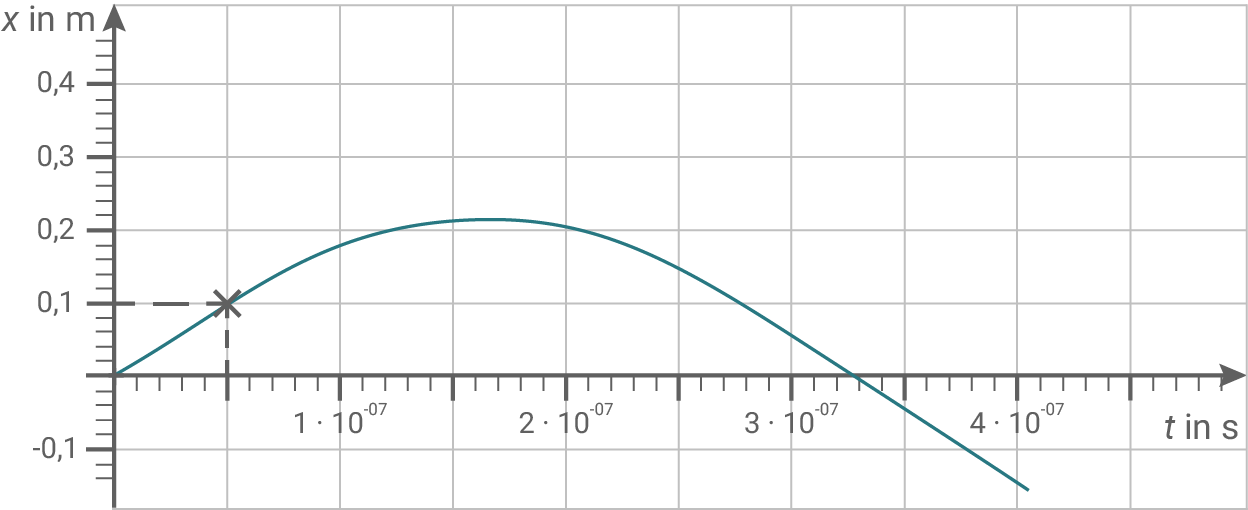
In Abbildung 2 entspricht die  -Achse dem Ort
-Achse dem Ort  in
in  des Elektrons. Somit kann auf der
des Elektrons. Somit kann auf der  -Achse der Zeitpunkt des Eintritts abgelesen werden:
-Achse der Zeitpunkt des Eintritts abgelesen werden:  Im Bereich
Im Bereich ![\([0; 0,5 \cdot 10^{-7}]\)](https://www.schullv.de/resources/formulas/08120a3c292453f813851cb28489a0cf3d46405f2d01c20b44b4fd702032db73_light.svg) verläuft der Graph für die Bewegung des Elektrons linear, d.h. das Elektron bewegt sich bis zum Eintritt in den Kondensator gleichförmig.
verläuft der Graph für die Bewegung des Elektrons linear, d.h. das Elektron bewegt sich bis zum Eintritt in den Kondensator gleichförmig.

Hilfsskizze: Koordinaten des Eintrittspunktes ablesen
2.2
Aus Abbildung 2 werden die Koordinaten des Hochpunktes am Graphen abgelesen:
Maximaler  -Wert:
-Wert:  Maximaler
Maximaler  -Wert:
-Wert: 
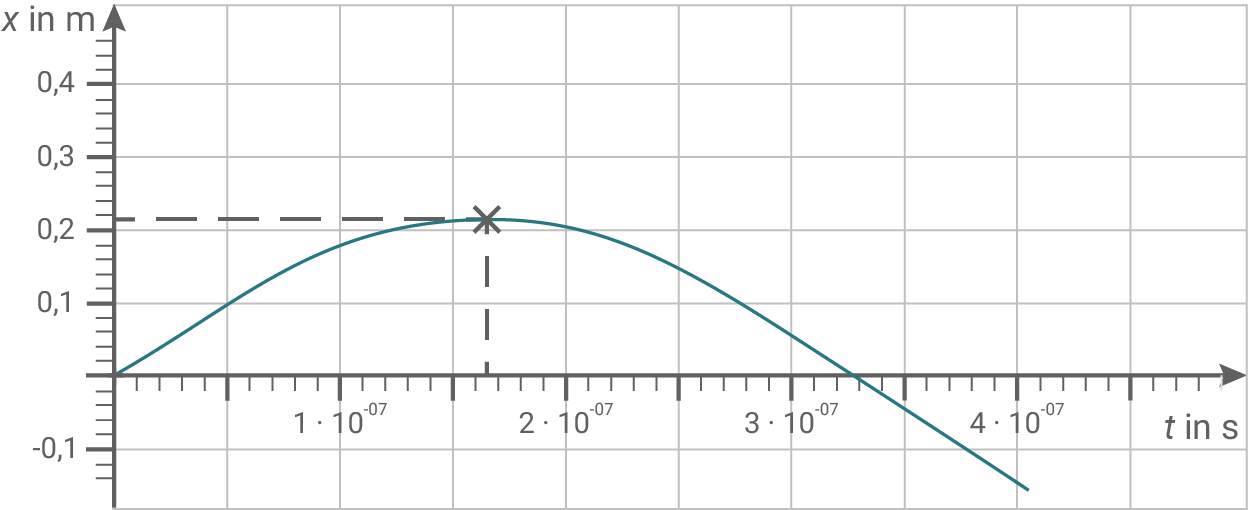
Hilfsskizze: Koordinaten des Hochpunktes ablesen
2.3
Vorüberlegungen aus dem Sachzusammenhang
(Zum Lösen der Aufgabe reicht der Rechenweg) Bei Eintritt in das elektrische Feld des Plattenkondensators bewegt sich das Elektron zunächst in Richtung der negativen Platte bis zum Zeitpunkt Das Elektron hat bei Eintritt in das homogene Feld eine Anfangsgeschwindigkeit
Das Elektron hat bei Eintritt in das homogene Feld eine Anfangsgeschwindigkeit  und somit Bewegungsenergie
und somit Bewegungsenergie 
 Somit gilt:
Alternativer Lösungsweg
Bis die Arbeit des elektrischen Feldes das Elektron vollständig abgebremst hat, durchläuft es das elektrische Feld bis
Somit gilt:
Alternativer Lösungsweg
Bis die Arbeit des elektrischen Feldes das Elektron vollständig abgebremst hat, durchläuft es das elektrische Feld bis  Danach bewegt sich das Elektron auf die positiv geladene Platte zu, wodurch die Arbeit
Danach bewegt sich das Elektron auf die positiv geladene Platte zu, wodurch die Arbeit  verrichtet wird.
Somit kann die vom elektrischen Feld verrichtete Arbeit alternativ als
verrichtet wird.
Somit kann die vom elektrischen Feld verrichtete Arbeit alternativ als  ausgedrückt werden.
Für die elektrische Feldkraft gilt:
ausgedrückt werden.
Für die elektrische Feldkraft gilt:
![\(\begin{array}[t]{rll}
F_{\text{el}}&=& E\cdot q \\[5pt]
&=& \dfrac{U}{d}\cdot e
\end{array}\)](https://www.schullv.de/resources/formulas/9c53c99002610458f1f2218ff1a0aef40058524a11b067359a94eddcd4bec8ac_light.svg) Daraus folgt:
Daraus folgt:
(Zum Lösen der Aufgabe reicht der Rechenweg) Bei Eintritt in das elektrische Feld des Plattenkondensators bewegt sich das Elektron zunächst in Richtung der negativen Platte bis zum Zeitpunkt
Innerhalb des homogenen Feldes des Plattenkondensators wirkt die durch das elektrische Feld verursachte elektrische Feldkraft  entgegengesetzt der Bewegungsrichtung des Elektrons, bremst das Elektron ab und lenkt es zur positiven Platte.
entgegengesetzt der Bewegungsrichtung des Elektrons, bremst das Elektron ab und lenkt es zur positiven Platte.
Das Elektron durchläuft somit nicht das gesamte eletrische Feld, sondern nur den Anteil Aus Abbildung 1 folgt der Abstand der Kondensatorplatten zu
Aus Abbildung 1 folgt der Abstand der Kondensatorplatten zu 
Das Elektron durchläuft somit nicht das gesamte eletrische Feld, sondern nur den Anteil

3.1.1
Das Neon-Atom nimmt zunächst  auf.
Durch Emission eines Quants geht es in den energetischen Zwischenzustand über.
Die abgegebene Energie ergibt sich wie folgt:
auf.
Durch Emission eines Quants geht es in den energetischen Zwischenzustand über.
Die abgegebene Energie ergibt sich wie folgt:
![\(\begin{array}[t]{rll}
\Delta E&=& h \cdot f \\[5pt]
&=& h\cdot \dfrac{c}{\lambda} \\[5pt]
&=& 4,14\cdot 10^{-15}\;\text{eVs}\cdot \dfrac{3\cdot 10^8\;\frac{\text{m}}{\text{s}}}{585\cdot 10^{-9}\;\text{m}}\\[5pt]
&\approx & 2,1 \;\text{eV}
\end{array}\)](https://www.schullv.de/resources/formulas/6c6dacca7d7328416a8e85ca76bb027ec558456c5d7f2f56cd6f0c75056ee643_light.svg)
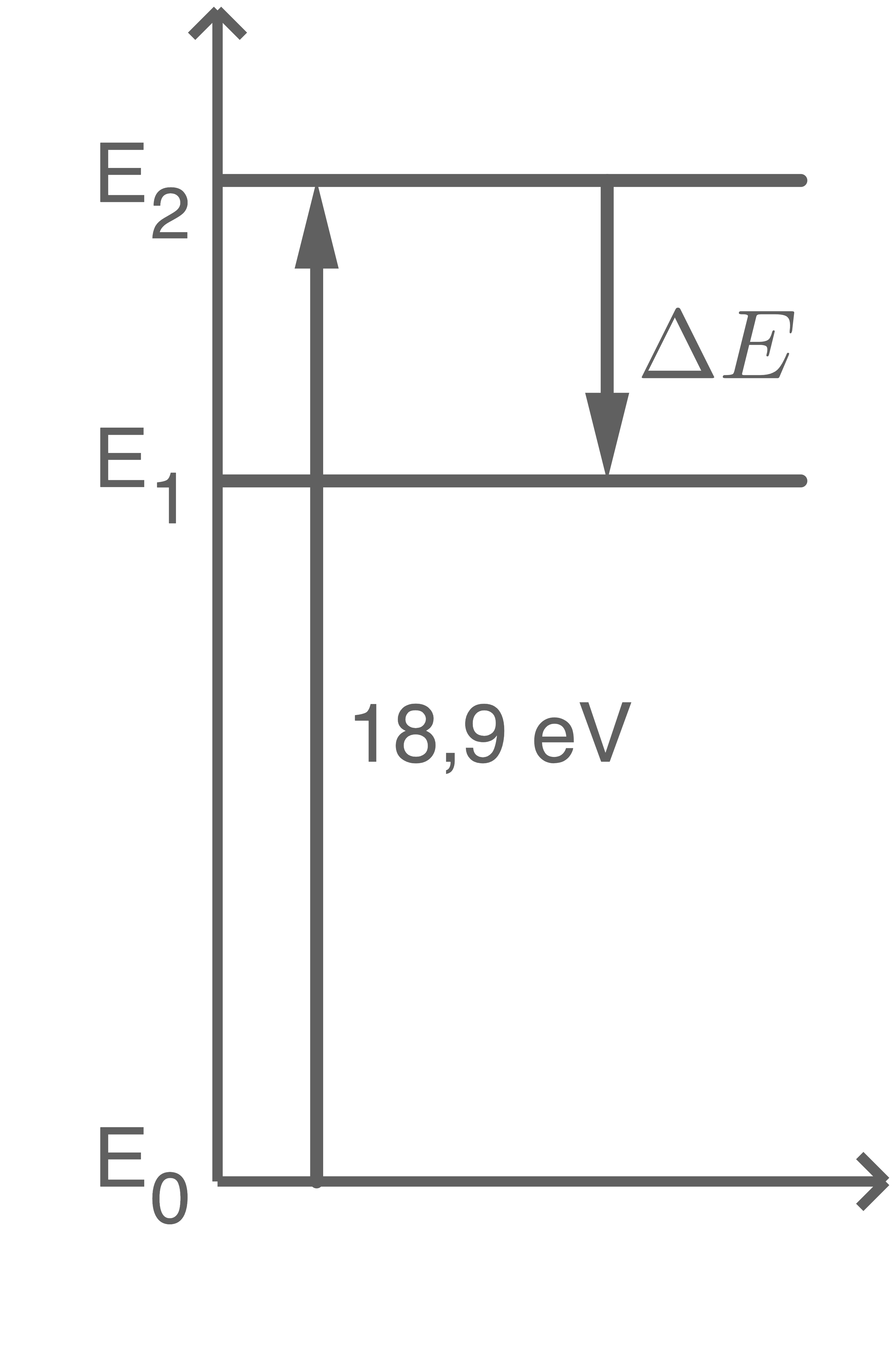
Hilfsskizze
3.1.2
Die Elektronen werden in einer mit Neongas gefüllten Röhre von Kathode zu Anode beschleunigt.
Die Elektronen stoßen dabei unabhängig von ihrer Energie mit den Gasatomen: elastisch und unelastisch.
Beim elastischen Stoß ergibt sich keine energetische Änderung.
Beim unealstischen Stoß kommt es zur Energieabsorption durch die Gasatome: Das Neon-Atom absorbiert ein Elektron mit selbigem Energiebetrag  Dadurch wird das Atom angeregt und in einen energetisch höheren Zustand versetzt. Jedoch ist dieser instabil, sodass das Atom ein Lichtquant mit dem Energiebetrag
Dadurch wird das Atom angeregt und in einen energetisch höheren Zustand versetzt. Jedoch ist dieser instabil, sodass das Atom ein Lichtquant mit dem Energiebetrag  abgibt. Dieser Energiebetrag entspricht der Wellenlänge orangefarbenen Lichtes.
Wird die Beschleunigungsspannung, an der die mit Neongas gefüllte Röhre anliegt, erhöht, so können die Eletronen erneut mit den Gasatomen unealstisch stoßen. Dadurch wiederholt sich der Vorgang und es ergibt sich ein zweiter orange leuchtender Bereich.
abgibt. Dieser Energiebetrag entspricht der Wellenlänge orangefarbenen Lichtes.
Wird die Beschleunigungsspannung, an der die mit Neongas gefüllte Röhre anliegt, erhöht, so können die Eletronen erneut mit den Gasatomen unealstisch stoßen. Dadurch wiederholt sich der Vorgang und es ergibt sich ein zweiter orange leuchtender Bereich.
3.2
Kontinuierlich wird dem Lasermedium Energie von einer Energiequelle zugeführt, wodurch zahlreiche Atome in einen angeregten und metastabilen Zustand versetzt werden.
Dieser Zustand gilt als metastabil, da die Verweildauer im angeregten Zustand deutlich länger als üblich ist.
Während spontaner Emission entsteht ein Lichtquant, welches beim Durchlaufen des Lasermediums eine Serie von induzierten Emissionen auslöst.
Eine Emission wird als induziert betrachtet, wenn der Übergang aus dem metastabilen Zustand durch ein Lichtquant gleicher Energie initiiert wird.
Dies führt dazu, dass alle emittierten Quanten kohärent sind, was bedeutet, dass sie identische Eigenschaften aufweisen.
Durch den optischen Resonator erfolgt eine Verstärkung der induzierten Emissionen, wodurch ein stark fokussierter Laserstrahl durch den teilweise durchlässigen Spiegel auf einer Seite austritt.
3.3.1
Elektronenbeugungsröhre
Elektronen, die aus der Glühkathode austreten, werden durch die Spannung  zur Anode beschleunigt. Sie durchdringen eine Schicht aus Grafitpulver und gelangen dann auf den Leuchtschirm der Vakuum-Röhre. Auf dem Schirm entstehen konzentrische Kreise. Diese werden als Interferenzbild einer Welle gedeutet, da Beugung bei Wellen auftritt.
Somit ergibt sich als Resumée aus dem Experiment: Elektronen besitzen Welleneigenschaften.
zur Anode beschleunigt. Sie durchdringen eine Schicht aus Grafitpulver und gelangen dann auf den Leuchtschirm der Vakuum-Röhre. Auf dem Schirm entstehen konzentrische Kreise. Diese werden als Interferenzbild einer Welle gedeutet, da Beugung bei Wellen auftritt.
Somit ergibt sich als Resumée aus dem Experiment: Elektronen besitzen Welleneigenschaften.
3.3.2