Teil B – Bewegungen, Induktion, Atom- und Kernphysik
1
Bewegungen
Im sächsischen Altenberg befindet sich eine Bobbahn. Beim Zweierbob erteilt der Pilot gemeinsam mit dem Anschieber dem Bob eine Anfangsgeschwindigkeit. Dazu schieben beide Sportler diesen aus der Ruhe heraus an und springen in den Bob. Der Pilot steuert den Bob durch kleine auf die Kufen übertragene Lenkbewegungen durch den Eiskanal.
Verschiedene grundlegende physikalische Prinzipien werden untersucht, die Vorgänge werden modellhaft vereinfacht.
Die Teilaufgaben 1.1 bis 1.4 sind unabhängig voneinander.
1.1
Eine Person der Masse 
springt mit der Geschwindigkeit 
auf einen ruhenden gleitfähigen Körper der Masse 
und bewegt sich gemeinsam mit diesem weiter.
Berechne die infolge der Wechselwirkung maximal mögliche Geschwindigkeit.
springt mit der Geschwindigkeit auf einen ruhenden gleitfähigen Körper der Masse und bewegt sich gemeinsam mit diesem weiter.
Berechne die infolge der Wechselwirkung maximal mögliche Geschwindigkeit.
Erreichbare BE-Anzahl: 02
1.2
Ein Körper der Masse gleitet aus der Ruhe heraus eine Ebene geradlinig hinab. Der Neigungswinkel beträgt 
die Gleitreibungszahl ist konstant 
Der Luftwiderstand wird vernachlässigt. Auf den Körper wirkt in Bewegungsrichtung zusätzlich zur Hangabtriebskraft eine konstante Schubkraft.
Die Zeit für das Zurücklegen der ersten 
beträgt 
Weise nach, dass die erreichte Geschwindigkeit 
beträgt.
Berechne den Betrag der Schubkraft.
gleitet aus der Ruhe heraus eine Ebene geradlinig hinab. Der Neigungswinkel beträgt die Gleitreibungszahl ist konstant
Der Luftwiderstand wird vernachlässigt. Auf den Körper wirkt in Bewegungsrichtung zusätzlich zur Hangabtriebskraft eine konstante Schubkraft.
Die Zeit für das Zurücklegen der ersten beträgt
Weise nach, dass die erreichte Geschwindigkeit beträgt.
Berechne den Betrag der Schubkraft.
Erreichbare BE-Anzahl: 04
1.3
Ein Körper gleitet geradlinig eine geneigte Ebene hinab, Gleitreibungskraft und Luftwiderstand werden nicht vernachlässigt.
1.3.1
Die Geschwindigkeit nimmt zu.
Zeige, dass sich bei einer Verdopplung der Geschwindigkeit die Luftreibungskraft vervierfacht.
Erreichbare BE-Anzahl: 02
1.3.2
Begründe, dass die Bewegung des Körpers im weiteren Verlauf gleichförmig werden kann.
Erreichbare BE-Anzahl: 02
1.4
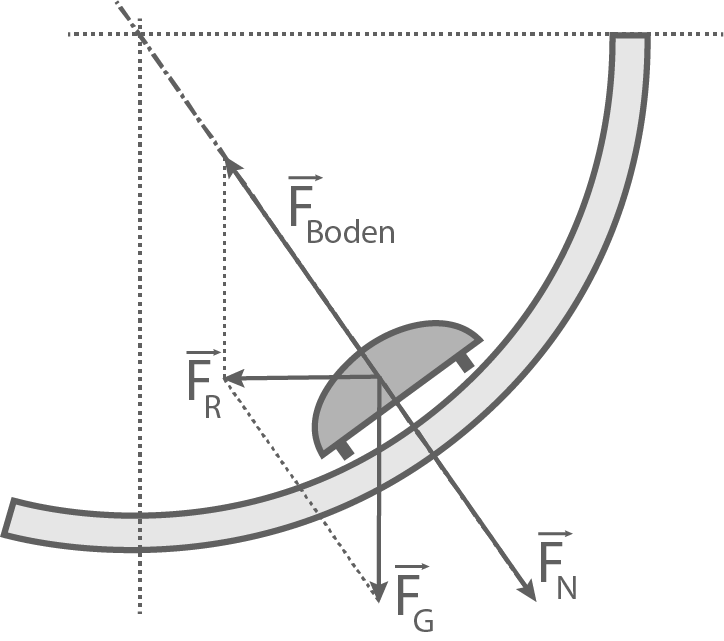
Ein Körper gleitet gleichförmig durch eine überhöhte Kurve. Körper und Bahn wechselwirken so, dass die Wirkungslinie der zugehörigen Kraft (siehe Abbildung) genau senkrecht zur Bahn gerichtet ist, der Körper gleitet somit in konstanter Bahnhöhe 
durch die Kurve.
Die Abbildung zeigt einen Querschnitt der Bahn.
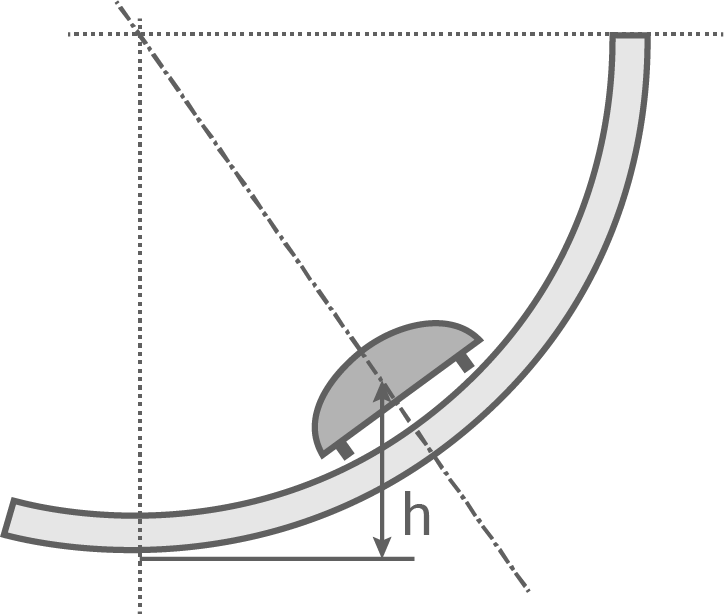Ergänze ein zugehöriges Kräfteparallelogramm und benenne die Kraftpfeile.
durch die Kurve.
Die Abbildung zeigt einen Querschnitt der Bahn.
Querschnitt der Bahn
Erreichbare BE-Anzahl: 03
2
Elektromagnetische Induktion
Ein System besteht aus einem Wagen aus Kunststoff, einer auf dem Wagen angebrachten offenen Leiterschleife und einer horizontal einseitig eingespannten Schraubenfeder. Der Wagen ist über einen Faden am anderen Ende der Feder befestigt und horizontal reibungsfrei beweglich. Ist das Ende der Feder am Ort 
, so ist die Feder entspannt.
Die Leiterschleife hat die Höhe 
und die Länge 
die Federkonstante beträgt 
Die Gesamtmasse des Wagens einschließlich der Leiterschleife beträgt 
, so ist die Feder entspannt.
Die Leiterschleife hat die Höhe und die Länge die Federkonstante beträgt
Die Gesamtmasse des Wagens einschließlich der Leiterschleife beträgt
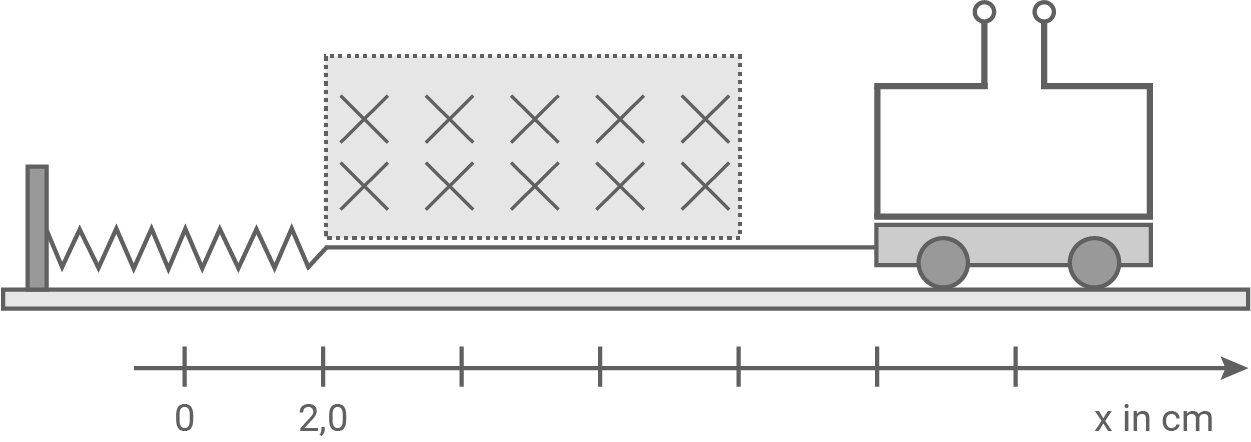
2.1
Die linke Kante des Wagens befindet sich am Ort 
Der Wagen wird freigegeben. Die Leiterschleife dringt in ein räumlich begrenztes, homogenes und zeitlich konstantes Magnetfeld der Flussdichte 
ein. Die Feldlinien zeigen senkrecht in die Zeichenebene.
Der Wagen wird freigegeben. Die Leiterschleife dringt in ein räumlich begrenztes, homogenes und zeitlich konstantes Magnetfeld der Flussdichte ein. Die Feldlinien zeigen senkrecht in die Zeichenebene.
2.1.1
Weise nach, dass der Wagen mit der Geschwindigkeit 
in das Magnetfeld eintritt.
in das Magnetfeld eintritt.
Erreichbare BE-Anzahl: 02
2.1.2
Berechne den Betrag der induzierten Spannung.
Erreichbare BE-Anzahl: 02
2.2
Die Feder wird entfernt. Die Leiterschleife wird vollständig vom Magnetfeld durchsetzt und ruht. Die Flussdichte nimmt gleichmäßig bis auf 
ab.
Skizziere die Graphen der Funktionen 
und 
über ein und derselben Zeitachse.
ab.
Skizziere die Graphen der Funktionen und über ein und derselben Zeitachse.
Erreichbare BE-Anzahl: 02
3
Grundlagen der Atomphysik
Die nachfolgende Abbildung zeigt schematisch für zwei Energiezustände 
und 
eines Atoms drei verschiedene Wechselwirkungen von Atom und Photon.
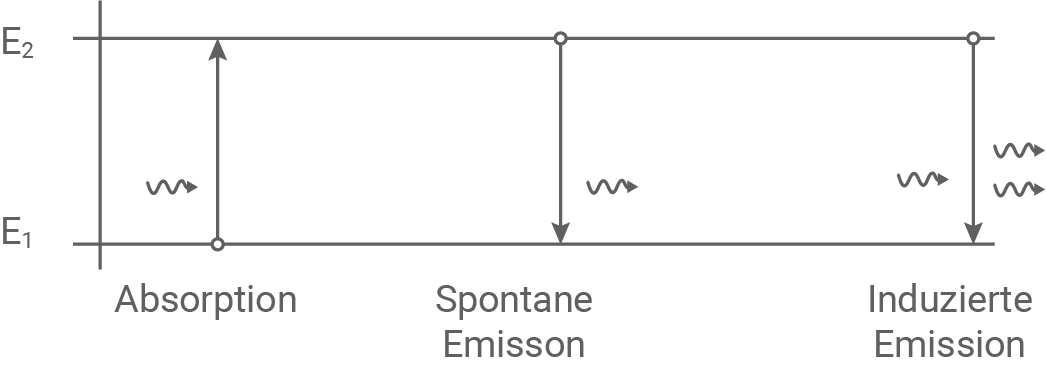Erläutere diese drei Vorgänge.
und eines Atoms drei verschiedene Wechselwirkungen von Atom und Photon.
Erreichbare BE-Anzahl: 04
4
Kernphysik
Heilbäder oder Heilstollen bieten oft eine Radontherapie an. Dabei wird die natürliche Freisetzung des radioaktiven Elementes Radon aus dem Erdboden genutzt. Die Therapie soll das menschliche Immunsystem stimulieren und dadurch Krankheiten lindern. Das Radon gelangt durch die Inhalation hochaktiver radonhaltiger Luft oder in Bädern durch die Haut in den menschlichen Organismus.
Radon-222 ist ein 
-Strahler und hat die Halbwertszeit 3,825 Tage.
-Strahler und hat die Halbwertszeit 3,825 Tage.
4.1
Gib die Kernumwandlungsgleichung für den Zerfall eines Radonkerns an.
Erreichbare BE-Anzahl: 01
4.2
Berechne die beim Zerfall eines Radonkerns freiwerdende Bindungsenergie.
Hinweis:
Atomare Masseneinheit: 
| Kernart | Kernmasse in  |
|---|---|
| Radon-222 | 221,97039991 |
| Tochterkern | 217,96289197 |
| -Teilchen |
4,00150608 |
Erreichbare BE-Anzahl: 02
4.3
Im Radonheilbad Bad Schlema gibt es radonhaltiges Wasser als natürliches Heilmittel. Pro Kubikmeter Wasser ist so viel Radon gelöst, dass die Aktivität 
erzeugt wird.
erzeugt wird.
4.3.1
Berechne die Masse des enthaltenen Radons.
Hinweis: Die Atommasse wird mit 
angenommen.
angenommen.
Erreichbare BE-Anzahl: 02
4.3.2
Ermittle, nach welcher Zeit die Anzahl der enthaltenen Rn-222-Nuklide auf 
gesunken ist, falls kein weiteres „frisches“ Radon-Wasser zugeführt wird.
gesunken ist, falls kein weiteres „frisches“ Radon-Wasser zugeführt wird.
Erreichbare BE-Anzahl: 02
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Es handelt sich um einen unelastischen Stoß. Mittels Impulserhaltungssatz, einsetzen der gegebenen Werte und umstellen nach der Geschwindigkeit folgt:
![\(\begin{array}[t]{rll}
m_P \cdot v_P +m_K \cdot v_K &=& (m_P+m_K)\cdot v_{\text{nach}} \\[5pt]
70\;\text{kg} \cdot 7,0 \;\frac{ \text{m} }{ \text{s}}+200 \;\text{kg} \cdot 0&=& (70\;\text{kg}+ 200\;\text{kg})\cdot v_{\text{nach}}\\[5pt]
70\;\text{kg} \cdot 7,0 \;\frac{ \text{m} }{ \text{s}}&=& 270\;\text{kg} \cdot v_{\text{nach}} &\quad \scriptsize \mid\; :270\;\text{kg} \\[5pt]
\dfrac{490\;\frac{ \text{m} }{ \text{s}}\cdot \text{kg} }{270\;\text{kg} }&=&v_{\text{nach}} \\[5pt]
1,8\;\frac{ \text{m} }{ \text{s}}&\approx& v_{\text{nach}} \\[5pt]
v_{\text{nach}}&\approx& 1,8 \;\frac{ \text{m} }{ \text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/6a04233e5777bdb9f3f57eb8ab7668ae651685ea430de9274605ab77782ae2d1_light.svg)
1.2
Alle wirkenden Kräfte besitzen konstante Beträge, weswegen es sich um eine gleichmäßig beschleunigte Bewegung handelt. Es gelten die Formeln für die gleichmäßig beschleunigte Bewegung.
Geschwindigkeitsnachweis
![\(\begin{array}[t]{rll}
s&=&\dfrac{1}{2}\cdot a \cdot t^2 &\quad \scriptsize \mid\;\cdot \frac{2}{t^2} \\[5pt]
s\cdot \dfrac{2}{t^2}&=& a \\[5pt]
a&=& s\cdot \dfrac{2}{t^2} \\[5pt]
&=& \dfrac{2\cdot 25 \;\text{m}}{(4,55\;\text{s})^2} \\[5pt]
&\approx & 2,415 \dfrac{\text{m}}{\text{s}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/8dc54fd8181e18b6dabd0a7c71fc0a34a65ed54f160422e967ff461596ba687c_light.svg)
Die Geschwindigkeit folgt zu
Betrag der Schubkraft berechnen
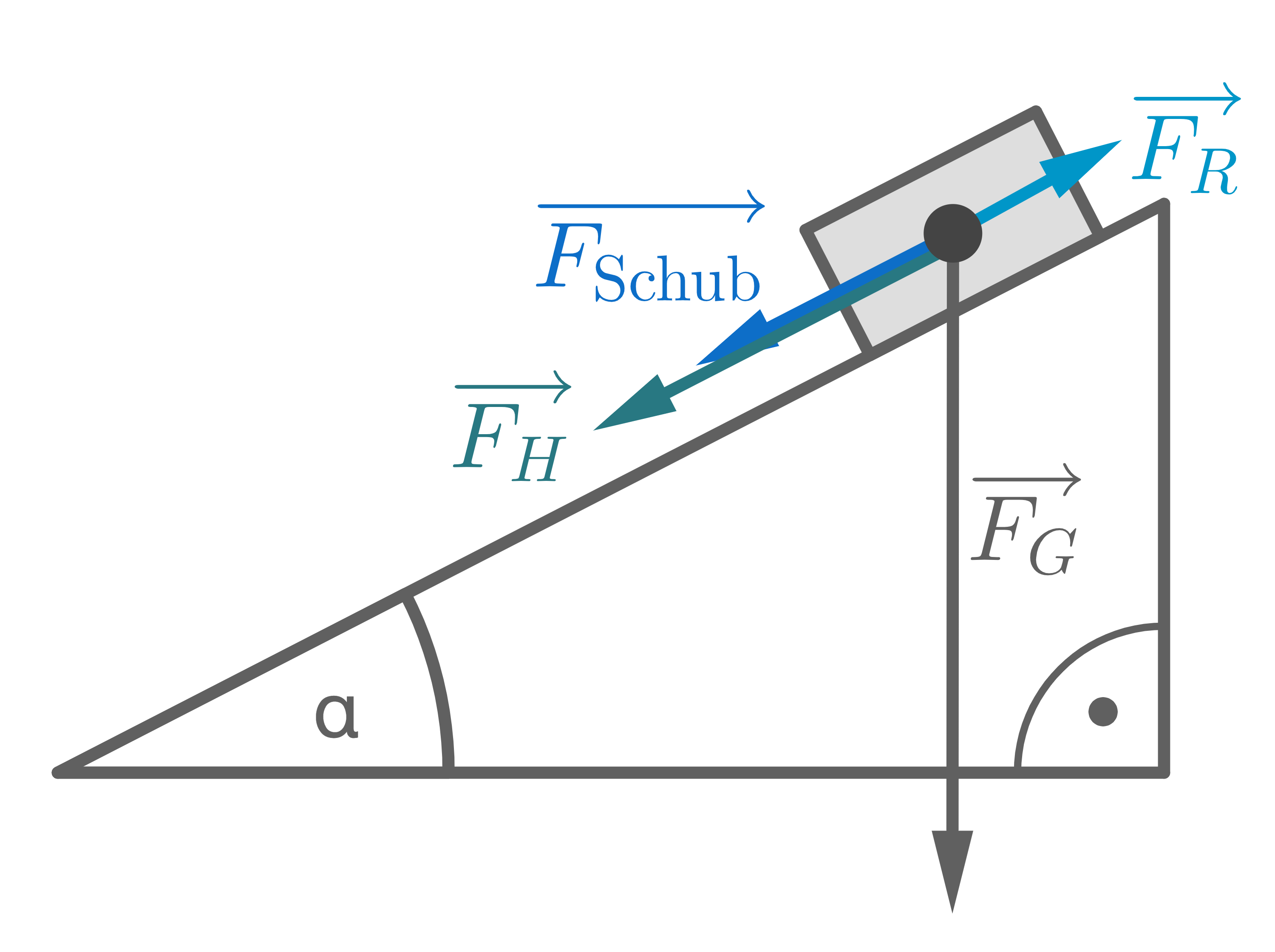
Lösungsweg über Berechnung der einzelnen Komponenten
Die beschleunigende (Gesamt-)Kraft setzt sich wie folgt zusammen:
Einsetzen und Umstellen:
Lösungsweg über Kräftebilanz
Die Geschwindigkeit folgt zu
Betrag der Schubkraft berechnen
Für die einzelnen Komponenten gilt:
Hilfsskizze: Wirkende Kräfte (nicht maßstäblich)
Die beschleunigende (Gesamt-)Kraft setzt sich wie folgt zusammen:
Einsetzen und Umstellen:
Lösungsweg über Kräftebilanz
![\(\begin{array}[t]{rll}
483 \;\text{N} &=& 341 \;\text{N} + F_{\text{Schub}} - 29\;\text{N} \\[5pt]
483 \;\text{N}&=& 312 \;\text{N}+ F_{\text{Schub}}&\quad \scriptsize \mid\;-312 \;\text{N} \\[5pt]
171 \;\text{N}&=& F_{\text{Schub}} \\[5pt]
F_{\text{Schub}}&=& 171 \;\text{N}
\end{array}\)](https://www.schullv.de/resources/formulas/ac074421be4f0f76abc270af86c12551388a65952bff50306c3d10e317980043_light.svg)
![\(\begin{array}[t]{rll}
F_{ges}&=& F_H + F_{\text{Schub}} - F_R \\[5pt]
m \cdot a &=& m\cdot g \cdot \sin(\alpha) + F_{\text{Schub}} - \mu \cdot m\cdot g \cdot \cos(\alpha) \\[5pt]
m \cdot a &=& m\cdot g \cdot (\sin(\alpha) -\mu \cdot \cos(\alpha)) + F_{\text{Schub}} \\[5pt]
200 \;\text{kg}\cdot 2,415 \;\frac{\text{m}}{\text{s}^2}&=& 200 \;\text{kg} \cdot 9,81 \;\frac{\text{m}}{\text{s}^2}\cdot (\sin(10^{\circ}) - 0,015 \cdot \cos(10^{\circ})) + F_{\text{Schub}} \\[5pt]
483 \;\text{N}&\approx& 312\;\text{N} + F_{\text{Schub}}&\quad \scriptsize \mid\; -312\;\text{N}\\[5pt]
312 \;\text{N}&=& F_{\text{Schub}}\\[5pt]
F_{\text{Schub}}&=& 312 \;\text{N}
\end{array}\)](https://www.schullv.de/resources/formulas/3d1eae424f13a14d1d4800dd7267ac298c2ff7cf6cfa9372c72e15e045d15038_light.svg)
1.3.1
Für den Betrag der Luftreibungskraft gilt:
Bei der Verdopplung der Geschwindigkeit, verändert sich keine andere Größe: 
und 
bleiben konstant. Somit beeinflusst ausschließlich die Geschwindigkeitsänderung die Luftreibungskraft.
womit die Luftreibungskraft quadratisch mit 
wächst. Wird also verdoppelt, so vervierfacht sich die Luftreibungskraft.
Lösung in Formeln (Alternativ)
Mit 
folgt:
![\(\begin{array}[t]{rll}
F_{\text{LR, neu} }&=& \dfrac{1}{2} \cdot A \cdot c_W \cdot \rho_{\text{Luft}} \cdot (2\cdot v)^2\\[5pt]
&=&\dfrac{1}{2} \cdot A \cdot c_W \cdot \rho_{\text{Luft}} \cdot 4\cdot v^2 \\[5pt]
&=& 4\cdot \underbrace{\dfrac{1}{2} \cdot A \cdot c_W \cdot \rho_{\text{Luft}} \cdot v^2}_{F_\text{ LR}}
\end{array}\)](https://www.schullv.de/resources/formulas/b387b32d42c7a5cf186bf58783593ba1c62584d8e3bd345a5dceee423b85c17f_light.svg)
Somit ist nachgewiesen, dass sich die Luftreibungskraft vervierfacht bei Verdopplung der Geschwindigkeit. Mathematisch: 
Bei der Verdopplung der Geschwindigkeit, verändert sich keine andere Größe: und bleiben konstant. Somit beeinflusst ausschließlich die Geschwindigkeitsänderung die Luftreibungskraft.
womit die Luftreibungskraft quadratisch mit wächst. Wird also verdoppelt, so vervierfacht sich die Luftreibungskraft.
Lösung in Formeln (Alternativ)
Mit folgt:
Somit ist nachgewiesen, dass sich die Luftreibungskraft vervierfacht bei Verdopplung der Geschwindigkeit. Mathematisch:
1.3.2
Bei einer gleichförmigen Bewegung gilt: 
Das erste Newtonische Gesetz (Trägheitsgesetz) besagt, dass die gleichförmige Bewegung der "Normalzustand" eines Körpers ist, für den es keine resultierende Kraft benötigt. Das heißt die wirkenden Kräfte gleichen sich gegenseitig aus.
Beim Herabgleiten des Körpers beschleunigt die Hangabtriebskraft den Körper, währenddessen wirken die Reibungskräfte (Luftreibungskraft und Gleitreibungskraft) entgegen.
Nur die Luftreibungskraft ist von abhängig. Somit könnte das Kräftegleichgwicht für eine bestimmte Geschwindigkeit eintreten.
Für eine bestimmte Geschwindigkeit kann die Bewegung gleichförmig werden.
Das erste Newtonische Gesetz (Trägheitsgesetz) besagt, dass die gleichförmige Bewegung der "Normalzustand" eines Körpers ist, für den es keine resultierende Kraft benötigt. Das heißt die wirkenden Kräfte gleichen sich gegenseitig aus.
Beim Herabgleiten des Körpers beschleunigt die Hangabtriebskraft den Körper, währenddessen wirken die Reibungskräfte (Luftreibungskraft und Gleitreibungskraft) entgegen.
Nur die Luftreibungskraft ist von abhängig. Somit könnte das Kräftegleichgwicht für eine bestimmte Geschwindigkeit eintreten.
Für eine bestimmte Geschwindigkeit kann die Bewegung gleichförmig werden.
1.4
Senkrecht zum Boden wirkt die Gewichtskraft 
Senkrecht zum Körper wirkt die Normalkraft 
Die Gegenkraft zur Normalkraft ist die Kraft, mit der der Boden auf den Bob wirkt: 
Aus dem Kräfteparallelogramm folgt die Radialkraft 
Senkrecht zum Körper wirkt die Normalkraft
Die Gegenkraft zur Normalkraft ist die Kraft, mit der der Boden auf den Bob wirkt:
Aus dem Kräfteparallelogramm folgt die Radialkraft
2.1.1
![\(\begin{array}[t]{rll}
E_{\text {Spann }}&=& E_{\text {kin}} \\[5pt]
\dfrac{1}{2} D \cdot s^2&=& \dfrac{1}{2}\cdot m \cdot v^2 \\[5pt]
\dfrac{1}{2} \cdot 2,4 \frac{ \text{N} }{ \text{m} } \cdot(0,020\; \text{m})^2&=& \dfrac{1}{2} \cdot 0,15 \;\text{kg} \cdot\left(0,080 \frac{\text{m} }{ \text{s} }\right)^2 \\[5pt]
4,8 \cdot 10^{-4} \;\text{J}&=& 4,8 \cdot 10^{-4} \;\text{J}
\end{array}\)](https://www.schullv.de/resources/formulas/3ea380e2238b81bde2a0f6a260f3d6125a57d0471860be78a538fb771b7cea1e_light.svg)
2.1.2
Eine Induktionsspannung folgt aus der zeitlichen Änderung des magnetischen Flusses.
Da die Leiterschleife gleichförmig in das Magnetfeld eindringt, folgt eine Änderung der Fläche der Leiterschleife. Aus dieser Flächenänderung folgt die Änderung des magnetischen Flusses.
![\(\begin{array}[t]{rll}
\left| U_{\text{ind}} \right|&=& -\dfrac{\mathrm d \Phi}{\mathrm d t} \\[5pt]
&=& -B\cdot \dfrac{\mathrm d A}{\mathrm d t} \\[5pt]
&=& -B\cdot \dfrac{\Delta A}{\Delta t}
\end{array}\)](https://www.schullv.de/resources/formulas/9a1a56a266da74b6d5cc0b8a87114c4c105279896fdb74d4a9573c5078fe7ff9_light.svg)
Zeit, die die Leiterschleife braucht, um vollständig in das Magnetfeld einzudringen:
![\(\begin{array}[t]{rll}
v&=& \dfrac{\Delta s}{\Delta t} \\[5pt]
\Delta t&=& \dfrac{\Delta s}{v} \\[5pt]
\Delta t&=& \dfrac{0,04 \;\text{m}}{0,08\;\frac{\text{m}}{\text{s}}} \\[5pt]
&=& 0,5\;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/d27cccf3c63a1694e83766488db9cedb494237cd0ab0928de475df8efa50ded4_light.svg)
Der Betrag der Induktionsspannung folgt mit den gegebenen Werten:
![\(\begin{array}[t]{rll}
\left| U_{\text{ind}} \right|&=&-B\cdot \dfrac{\Delta A}{\Delta t} \\[5pt]
&=& -0,065\;\text{T} \cdot \dfrac{0,02 \;\text{m}\cdot 0,04\;\text{m}}{0,5\;\text{s}} \\[5pt]
&=& 0,0001\;\text{V}
\end{array}\)](https://www.schullv.de/resources/formulas/f18383d5b8f65bbb79ba0462bba5a0be087bfa3c5c129827516e7090202931ed_light.svg)
Da die Leiterschleife gleichförmig in das Magnetfeld eindringt, folgt eine Änderung der Fläche der Leiterschleife. Aus dieser Flächenänderung folgt die Änderung des magnetischen Flusses.
Zeit, die die Leiterschleife braucht, um vollständig in das Magnetfeld einzudringen:
Der Betrag der Induktionsspannung folgt mit den gegebenen Werten:
2.2
Überlegungen
Eine Induktionsspannung folgt aus der zeitlichen Änderung des magnetischen Flusses.
Der magnetische Fluss ändert sich auch durch eine Magnetfeldänderung.
Es gilt: 
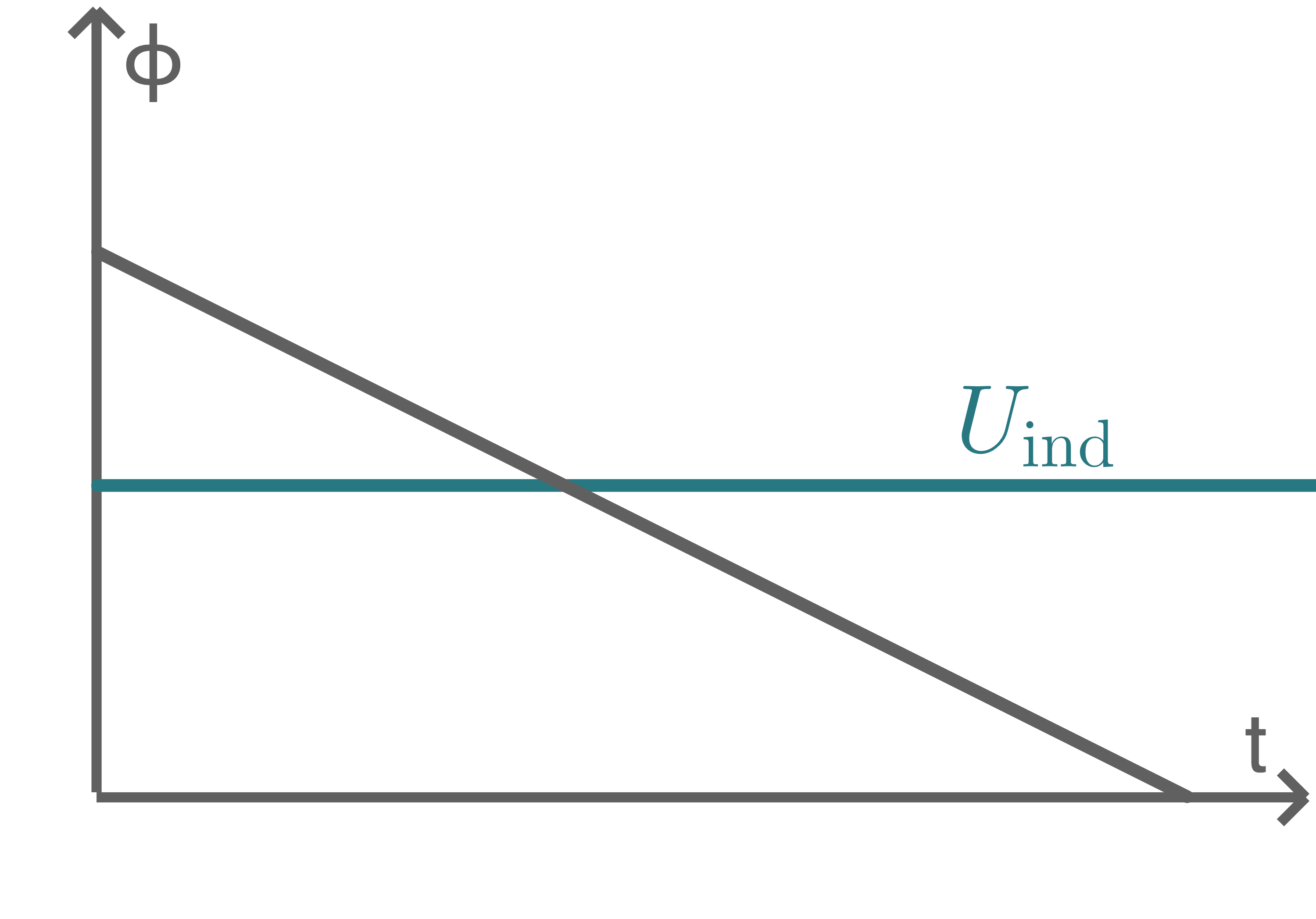
Die magnetische Flussdichte nimmt gleichmäßig auf 
ab, woraus sich eine fallende Gerade ergibt und die Induktionsspannung ist konstant.
Skizze der Graphen der Funktionen
Die magnetische Flussdichte nimmt gleichmäßig auf ab, woraus sich eine fallende Gerade ergibt und die Induktionsspannung ist konstant.
Skizze der Graphen der Funktionen
3
Absorption
Durch den Quantensprung eines Elektrons im Atom wird ein Photon absorbiert und das Atom in einen energetisch höheren Zustand.
Ein Atom kann ein Photon aufnehmen, wenn das Photon den Energiebetrag, der der Differenz der Energiestufen des Atoms entspricht, besitzt. (Bohr'sches Atommodell)
Danach ist das Atom in einem energetisch angeregten, höherem Zustand.
Spontane Emission
Spontane Emission ist der umgekehrte Vorgang zur Absorption. Ein Elektron geht spontan aus einem höheren in einen tieferen Energiezustand über. Der Zustand der spontanen Emission eines Photons in einem angeregten Atom ist instabil.
Das Atom gibt ein Photon ab, dies entspricht dem Energiebetrag der Differenz zweier Energiestufen des Atoms.
Das Atom geht vom angeregten Zustand 
in den Grundzustand 
über.
Induzierte Emission
Ein Photon erzwingt eine Emission bei einem sich im metastabilen Zustand befindlichen Atom.
Ein Atom kehrt dabei aus einem höheren in einen tieferen Energiezustand zurück. Die Energie des eingestrahlten Photons muss gleich der Energiedifferenz dieser Zustände sein.
Vom Photon wird die Energieabgabe des Atoms stimuliert.
So werden zwei gleiche Photonen emittiert: das eine aus dem Energieunterschied wie bei der spontanen Emission und das andere aus der Anregung.
Beide Photonen besitzen identische Eigenschaften.
Danach ist das Atom in einem energetisch angeregten, höherem Zustand.
Spontane Emission
Spontane Emission ist der umgekehrte Vorgang zur Absorption. Ein Elektron geht spontan aus einem höheren in einen tieferen Energiezustand über. Der Zustand der spontanen Emission eines Photons in einem angeregten Atom ist instabil.
Das Atom gibt ein Photon ab, dies entspricht dem Energiebetrag der Differenz zweier Energiestufen des Atoms.
Das Atom geht vom angeregten Zustand in den Grundzustand über.
Induzierte Emission
Ein Photon erzwingt eine Emission bei einem sich im metastabilen Zustand befindlichen Atom.
Ein Atom kehrt dabei aus einem höheren in einen tieferen Energiezustand zurück. Die Energie des eingestrahlten Photons muss gleich der Energiedifferenz dieser Zustände sein.
Vom Photon wird die Energieabgabe des Atoms stimuliert.
So werden zwei gleiche Photonen emittiert: das eine aus dem Energieunterschied wie bei der spontanen Emission und das andere aus der Anregung.
Beide Photonen besitzen identische Eigenschaften.
4.1
4.2
Für den Massedefekt gilt:
Bindungsenergie mittels Einsteins Masse-Energie-Beziehung berechnen:
![\(\begin{array}[t]{rll}
\Delta m&=&m_{ \text{Po} -218}+m_\alpha-m_{ \text{Rn} -222} \\[5pt]
&=& 217,96289197 u +4,00150608 u -221,97039991 u \\[5pt]
&=& -0,00600186 u \\[5pt]
&=& -9,966322603 \cdot 10^{-30} \;\text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/9c609837c8129122929b0ce7df5fbecf471a4ca7993e6d6f8490fab207557153_light.svg)
![\(\begin{array}[t]{rll}
\left|\Delta E_{ B }\right|&=& |\Delta m| \cdot c^2 \\[5pt]
&=& 9,966322603 \cdot 10^{-30} \;\text{kg} \cdot\left(2,998 \cdot 10^8 \frac{ \text{m} }{ \text{s} }\right)^2 \\[5pt]
&=& 8,958 \cdot 10^{-13} \;\text{J} \\[5pt]
&=& 5,6 \;\text{MeV}
\end{array}\)](https://www.schullv.de/resources/formulas/20a04f6f0d890faef22065b94935813373a9b586f38775f58aa34195b179184a_light.svg)
4.3.1
1. Schritt: Berechnung der Anzahl der Radonkerne
2. Schritt: Masse der Radonkerne berechnen
![\(\begin{array}[t]{rll}
A&=& \lambda \cdot N&\quad \scriptsize \mid\;:\lambda \\[5pt]
\dfrac{A}{\lambda}&=& N \\[5pt]
N &=& \dfrac{A}{\lambda}&\quad \scriptsize \mid\;\lambda=\frac{\ln (2)}{T_{1/2}} \\[5pt]
&=&\dfrac{A\cdot T_{1/2}}{\ln (2)}\\[5pt]
&=&\dfrac{1 \cdot 10^5 \frac{1}{\text{s} } \cdot 3,825 \cdot 24 \cdot 3600 \;\text{s} }{\ln (2)} \\[5pt]
&=& 4,7678 \cdot 10^{10}
\end{array}\)](https://www.schullv.de/resources/formulas/39a89ff43f21b767df915be11ae999fdd96d31930f4223b5eda8e950f599b594_light.svg)
![\(\begin{array}[t]{rll}
m&=& N\cdot 222u\\[5pt]
&=& 4,7678 \cdot 10^{10} \cdot 222 \cdot 1,660539 \cdot 10^{-27} \;\text{kg} \\[5pt]
&=& 1,76\cdot 10^{-14}\;\text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/e05e5eaf21b0642ea4c725abc1f75c9cd1cc65bbcb03f68b98d0f42c87ed4215_light.svg)
4.3.2
Zerfallszeit mittels Halbwertszeit ermitteln
Zerfallszeit mittels Zerfallskonstante ermitteln (Alternativ)
![\(\begin{array}[t]{rll}
N(t)&=& N_0 \cdot\left(\frac{1}{2}\right)^{\frac{t}{T_{1 / 2}}} &\quad \scriptsize \mid\;:N_0 \\[5pt]
\dfrac{N(t)}{N_0}&=& \left(\dfrac{1}{2}\right)^{\frac{t}{T_{1 / 2}}} \\[5pt]
0,15&=& \left(\dfrac{1}{2}\right)^{\frac{t}{3,825d}} \\[5pt]
\log_{0,5}(0,15)&=& \dfrac{t}{3,825d}&\quad \scriptsize \mid\;\cdot 3,825d \\[5pt]
\log_{0,5}(0,15)\cdot 3,825d&=& t \\[5pt]
10,5 d&\approx& t \\[5pt]
t&\approx& 10,5 d
\end{array}\)](https://www.schullv.de/resources/formulas/5ce9905bc793e84e0f51409495e605cc9e6745babae04ff9c542205590a43ebe_light.svg)
![\(\begin{array}[t]{rll}
N(t)&=& N_0 \cdot \mathrm e^{-\lambda\cdot t}\\[5pt]
\dfrac{N(t)}{N_0}&=& \mathrm e^{-\lambda\cdot t} \\[5pt]
0,15&=&\mathrm e^{-\lambda\cdot t} &\quad \scriptsize \mid\;\ln(\;) \\[5pt]
\ln(0,15)\dfrac{}{}&=& -\lambda\cdot t &\quad \scriptsize \mid\;:( -\lambda) \\[5pt]
\dfrac{\ln(0,15)}{-\lambda}&=&t \\[5pt]
t&=& \dfrac{\ln(0,15)}{-\ln(2)}\cdot T_{1/2} \\[5pt]
&=& \dfrac{\ln(0,15)}{-\ln(2)}\cdot 3,825d \\[5pt]
&\approx& 10,5 d
\end{array}\)](https://www.schullv.de/resources/formulas/02a7780b0f4759220569ff840ca42e51290216fad95299103211dacaf8504b85_light.svg)