Teil B – Bewegungen, kleinste Teilchen

Bewegungen, Energie, mechanische Arbeit, Impuls

Skateboarding ist eine Sportart, bei der eine Vielzahl physikalischer Gesetze zur Anwendung kommt. Ziel dieser Sportart ist die Beherrschung möglichst vieler und möglichst schwieriger „Tricks“ an unterschiedlichsten „Spots“ (Hindernissen) im öffentlichen Raum, in Skateparks oder in Skatehallen.

sachsen physik abi lk 2023 teil b abbildung 1 skatepark halfpipe skateboard

Das Sportgerät hat die Form eines Bretts, an dessen Unterseite vier Rollen angebracht sind (engl. Skateboard). Auf diesem steht der Skater, fährt und führt Sprünge, Drehungen usw. aus.

sachsen physik abi lk 2023 teil b abbildung 1 skatepark skateboard

Skateboarding bedeutet für Skater jedoch wesentlich mehr als Sport. Für sie ist Skateboarding mit einem bestimmten Lebensgefühl verknüpft.

1.1

Ein Skateboard rollt auf einer horizontalen Unterlage. Der Skater läuft hinter dem Board her und springt in Bewegungsrichtung auf. Er bewegt sich dadurch auf dem Board stehend weiter. Der Vorgang wird modellhaft als gerader unelastischer Stoß betrachtet. Vor dem Stoß beträgt die Geschwindigkeit des Skaters $5,0\,\text m \cdot \text s ^{-1}$ , die des Skateboards beträgt $2,2\,\text m \cdot \text s ^{-1}$ . Der Skater hat die Masse $65\,\text{kg}.$

Unmittelbar nach dem Stoß bewegen sich beide gemeinsam mit der Geschwindigkeit $4,9\,\text m \cdot \text s ^{-1}$ .

1.1.1

Beschreibe die zugehörigen Energieumwandlungen.

Erreichbare BE-Anzahl: 03

1.1.2

Leite allgemein ausgehend vom Impulserhaltungssatz und den gegebenen Größen eine Gleichung zur Berechnung der Masse des Skateboards her.

Erreichbare BE-Anzahl: 02

1.1.3

Gib die Masse des Skateboards an.

Erreichbare BE-Anzahl: 01

1.2

Der Skater fährt auf einer horizontalen Bahn auf eine viertelkreisförmige abwärts verlaufende Bahn zu. Die Abbildung zeigt das Prinzip.

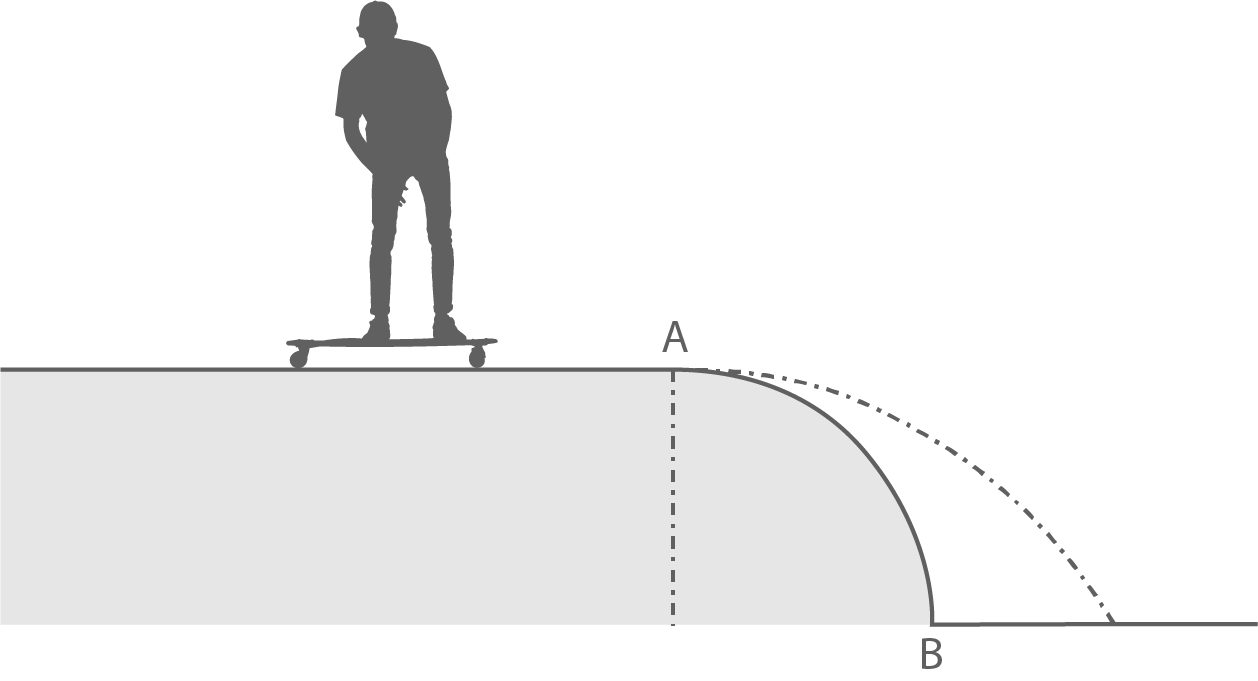sachsen physik abi lk 2023 teil b abbildung 3 skateboarder

Der Vorgang wird modellhaft vereinfacht.

Skater und Board werden durch einen als Massepunkt definierten reibungsfrei gleitenden Körper beschrieben. Der Viertelkreis hat den Radius $r=1,5\,\text m$ .

1.2.1

Der Körper muss mit einer Mindestgeschwindigkeit gleiten, damit er unmittelbar nach Durchlaufen des Ortes A nicht mehr auf die Bahn drückt.

Weise rechnerisch nach, dass diese Mindestgeschwindigkeit $3,8\,\text m \cdot \text s ^{-1}$ beträgt.

Erreichbare BE-Anzahl: 02

1.2.2

Der Körper gleitet mit der Geschwindigkeit $4,5\,\text m \cdot \text s ^{-1}$ und führt einen horizontalen Wurf aus.

Ermittle die Entfernung des Auftreffortes vom Ort B.

Erreichbare BE-Anzahl: 03

Geladene Teilchen im elektrischen Feld - Äußerer lichtelektrischer Effekt

2.1

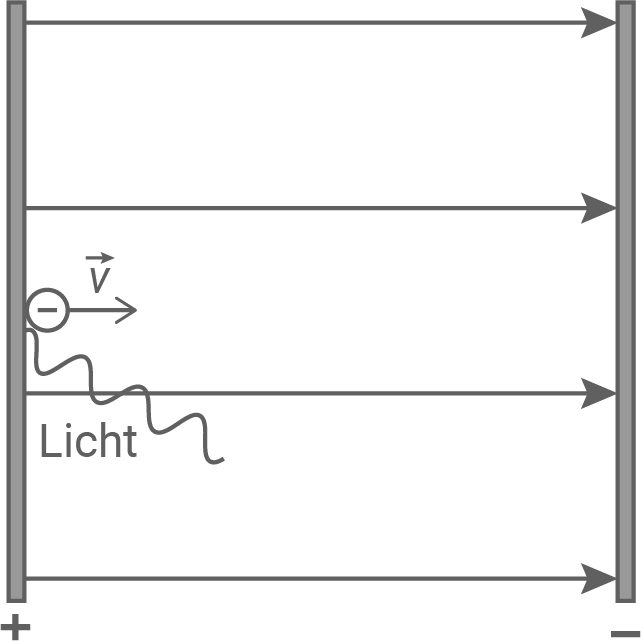
Um die kinetische Energie der von Licht aus einer metallischen Oberfläche herausgelösten Elektronen zu ermitteln, ist nachfolgendes Prinzip geeignet: Ein Plattenkondensator ist auf die Spannung $U$ geladen. Die herausgelösten Elektronen treten parallel zu den Feldlinien mit der Geschwindigkeit $v$ in das homogene elektrische Feld des Plattenkondensators (Plattenabstand $d$ ) ein. Sie werden im elektrischen Gegenfeld auf die Geschwindigkeit $0\,\text m \cdot \text s ^{-1}$ abgebremst und kehren, um.

sachsen physik abi lk 2023 teil b abbildung 4 kinetische energie von licht

2.1.1

Die Entfernung $\text s$ des Umkehrpunktes von der positiv geladenen Platte wird gemessen. Leite eine Gleichung $v=v(U, s, d)$ für die Eintrittsgeschwindigkeit eines Elektrons her.

Erreichbare BE-Anzahl: 03

2.2.2

Für ein herausgelöstes Elektron gilt bei $U=1,2\,\text V,$ dass die Entfernung $\text s$ des Umkehrpunktes gleich dem Plattenabstand $d$ ist. Gib die kinetische Energie dieses Elektrons an.

Erreichbare BE-Anzahl: 01

2.2

Licht verschiedener Wellenlängen trifft auf ein Metall und löst Elektronen heraus. Die maximale kinetische Energie der herausgelösten Elektronen wird gemessen.

$\color{#fff}{\lambda}$ in $\color{#fff}{\text{nm}}$	$\color{#fff}{E_{\text{kin, max}}}$ in $\color{#fff}{\text{eV}}$
447	1,37
471	1,23
502	1,07
668	0,46
707	0,36

Ermittle unter Nutzung aller Messwertpaare sowie einer geeigneten Regression die Austrittsarbeit für dieses Metall und das Planck'sche Wirkungsquantum.

Erreichbare BE-AnzahI: 04

Positronen-Emissions-Tomographie

Kupfer ist als ein rötlich glänzendes Metall bekannt. Einige Cu-Isotope sind aber auch radioaktiv. So ist z. B. das Isotop Cu-64 ein $\beta^{+}$ - Strahler und wird in der nuklearmedizinischen Diagnostik im Helmholtz-Zentrum Dresden-Rossendorf angewandt. Cu-64 hat die Halbwertszeit 12,701 Stunden.

Bei einer Positronen-Emissions-Tomographie beträgt die Aktivität des genutzten Präparates zu Beginn der Untersuchung $1,0 \cdot 10^9\,\text{Bq}.$

3.1

Das Prinzip der Massenspektroskopie ist geeignet, um nachzuweisen, dass Cu-64 ein $\beta^{+}$ - Strahler ist.

Erläutere das Prinzip.

Erreichbare BE-Anzahl: 03

3.2

Gib die vollständige Kernumwandlungsgleichung für den Zerfall eines Cu-64-Kerns an.

Erreichbare BE-Anzahl: 01

3.3

Ermittle rechnerisch die zu Beginn der Untersuchung erforderliche Anzahl der im Präparat enthaltenen Cu-64 Kerne.

Erreichbare BE-Anzahl: 02

3.4

Weise rechnerisch nach, dass die bei einem $\beta^{+}$ - Zerfall freiwerdende Energie $0,65\,\text{MeV}$ beträgt.

Erreichbare BE-Anzahl: 02

3.5

Berechne den Betrag der Bindungsenergie pro Nukleon für Cu-64.

Erreichbare BE-Anzahl: 03

Hinweis für Aufgabe 3:

Teilchen	Masse in $\color{#fff}{u}$
Positron	$5,485799 \cdot 10^{-4}$
Proton	$1,007287$
Neutron	$1,008665$
Nuklid	Kernmasse in $u$
Cu-64	$63,91386$
Tochterkern beim $\beta^{+}$ - Zerfall von Cu-64	$63,91261$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1.1

Beim beschriebenen Vorgang des Skaters, der auf das rollende Skateboard springt, finden verschiedene Energieumwandlungen statt. Vor dem Stoß:

Beim beschriebenen Vorgang, bei dem der Skater auf das rollende Skateboard springt, finden verschiedene Energieumwandlungen statt. Vor dem Stoß besitzt der Skater eine kinetische Energie aufgrund seiner Geschwindigkeit, während das Skateboard ebenfalls eine kinetische Energie aufgrund seiner eigenen Geschwindigkeit besitzt.

Während des Stoßes kommt es zu einer Verformung, die als unelastischer Stoß modelliert wird. Bei diesem Stoß wird ein Teil der kinetischen Energie des Skaters in innere Energie umgewandelt, da Verformungen und Reibungskräfte zwischen den Objekten auftreten. Auch die kinetische Energie des Skateboards wird teilweise in innere Energie umgewandelt.

Nach dem Stoß bewegen sich der Skater und das Skateboard gemeinsam mit einer neuen Geschwindigkeit. Die kinetische Energie des Systems, bestehend aus Skater und Skateboard, hat sich aufgrund des unelastischen Stoßes verringert. Ein Teil der ursprünglichen kinetischen Energie wurde in andere Energieformen umgewandelt, wie beispielsweise Wärme durch Reibung oder Verformung.

1.1.2

$m_B$ entspricht der Masse des Boards, $m_S$ der Masse des Skaters, $v_{S,\text{vor}}$ der Geschwindikeit des Skaters vor dem Stoß, $v_{B,\text{vor}}$ der Geschwindigkeit des Boards vor dem Stoß und $v_{\text{neu}}$ entpricht der Geschwindigkeit des Skaters auf dem Bord nach dem Stoß.

Mit dem Impulserhaltungssatz gilt:

Rechenweg anzeigen

$m_B= \dfrac{m_S\cdot v_{\text{neu}} - m_S\cdot v_{S,\text{vor}}}{\left(v_{B,\text{vor}}- v_{\text{neu}} \right)}$

1.1.3

Einsetzen der Werte in die hergeleitete Gleichung liefert für die Masse des Boards $m_B:$

$\begin{array}[t]{rll} m_B&=& \dfrac{m_S\cdot v_{\text{neu}} - m_S\cdot v_{S,\text{vor}}}{\left(v_{B,\text{vor}}- v_{\text{neu}} \right)} &\quad \scriptsize \\[5pt] &=& \dfrac{65 \;\text{kg}\cdot 4,9 \;\dfrac{\text{m}}{\text{s}} - 65 \;\text{kg}\cdot 5,0\;\dfrac{\text{m}}{\text{s}}}{\left( 2,2 \;\dfrac{\text{m}}{\text{s}}- 4,9 \;\dfrac{\text{m}}{\text{s}} \right)} &\quad \scriptsize \\[5pt] &=& 2,4 \;\text{kg} \end{array}$

1.2.1

Da der Skater den Kontakt zur Bahn verliert und nicht mehr auf die Bahn gedrückt wird, sind die Normal- und Reibungskraft Null. Der einzige wirkende Kraftvektor ist die Gewichtskraft $F_G$ , die senkrecht nach unten zeigt. Um den Skater auf der Bahn zu halten, muss die Zentripetalkraft $F_Z$ gleich oder größer als die Gewichtskraft sein. Für die Zentripetalkraft gilt:

$\begin{array}[t]{rll} F_Z&=& m \cdot a_Z &\quad \scriptsize \mid\; a_Z = \frac{v^2}{r} \\[5pt] &=& m \cdot \frac{v^2}{r} \end{array}$

Damit der Skater den Ort A passieren kann, muss die Zentripetalkraft größer oder gleich der Gewichtskraft sein:

$\begin{array}[t]{rll} F_Z &\geq& F_G &\quad \scriptsize \\[5pt] m \cdot \frac{v^2}{r}&\geq& m\cdot g &\quad \scriptsize \mid\;\cdot \dfrac{1}{m} \\[5pt] \frac{v^2}{r}&\geq& g &\quad \scriptsize \mid\;\cdot r \\[5pt] v^2&\geq& g \cdot r&\quad \scriptsize \mid\; \sqrt{\;} \\[5pt] v&\geq& \sqrt{g \cdot r} \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} v&\geq& \sqrt{g \cdot r} &\quad \scriptsize \\[5pt] &=& \sqrt{9,81 \;\dfrac{\text{m}}{\text{s}^2}\cdot 1,5\;\text{m}} &\quad \scriptsize \\[5pt] &=& \sqrt{ 14,7\;\dfrac{\text{m}^2}{\text{s}^2}} &\quad \scriptsize \\[5pt] &=& 3,8\;\dfrac{\text{m}}{\text{s}} \end{array}$

1.2.2

Gesucht ist die Flugweite in $x$ -Richtung abzüglich des Kreisradius von $1,5 \;\text{m}.$

Der Körper führt einen horizontalen Wurf aus. Hierbei gilt für die Bewegungen:

$\boldsymbol{x}$ -Richtung

$\overrightarrow{v_x}= 4,5 \;\dfrac{\text{m}}{\text{s}}$

$s_x= v_x \cdot t$

$\boldsymbol{y}$ -Richtung

Freier Fall aus der Höhe $h$

$\begin{array}[t]{rll} h&=& \dfrac{1}{2}\cdot g\cdot t^2 &\quad \scriptsize \mid\;\cdot \frac{2}{g} \\[5pt] \dfrac{2\cdot h}{g}&=& t^2&\quad \scriptsize \mid\;\sqrt{\;} \\[5pt] \sqrt{\dfrac{2\cdot h}{g}}&=& t \\[5pt] t&=&\sqrt{\dfrac{2\cdot h}{g}} \end{array}$

$t$ einsetzen in $s_x:$

$\begin{array}[t]{rll} s_x&=& v_x \cdot t \\[5pt] s_x&=&v_x \cdot \sqrt{\dfrac{2\cdot h}{g}} \\[5pt] s_x&=& 4,5 \;\frac{\text{m}}{\text{s}} \cdot \sqrt{\dfrac{2\cdot 1,5 \;\text{m}}{9,81\;\frac{\text{m}}{\text{s}^2}}} \\[5pt] &\approx & 2,49 \;\text{m} \end{array}$

Die Entfernung des Auftreffortes vom Punkt $B$ ergibt sich zu $2,49 \;\text{m} -1,5 \;\text{m}=0,99 \;\text{m} \approx 1 \;\text{m}.$

2.1.1

$\begin{array}[t]{rll} F_{el}&=& q\cdot E &\quad \scriptsize \\[5pt] a\cdot m_e&=& e\cdot E &\quad \scriptsize \mid\; E=\dfrac{U}{d} \\[5pt] a\cdot m_e&=& e\cdot \dfrac{U}{d} &\quad \scriptsize \mid\; \dfrac{1}{m_e} \\[5pt] a&=& \dfrac{e\cdot U}{d \cdot m_e} \end{array}$

Für die gleichmäßig beschleunigte Bewegungsgleichung des Elektrons gilt:

Rechenweg anzeigen

$\sqrt{\dfrac{2\cdot s\cdot d\cdot m_e }{q\cdot U}}= t$

Für die Austrittsgeschwindigkeit des Elektrons gilt:

Rechenweg anzeigen

$v=\sqrt{\dfrac{2e\cdot U\cdot s}{d \cdot m_e} }$

2.1.2

Für die kinetische Energie des Elektrons gilt:

Rechenweg anzeigen

$E_{\text{kin}}= e\cdot U$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} E_{\text{kin}}&=& e\cdot U&\quad \scriptsize \\[5pt] &=& 1,2 \;e\text{V} \\[5pt] \end{array}$

2.2.1

Die Energiebilanz lässt sich auch wie folgt ausdrücken:

$\begin{array}[t]{rll} E_{\text{kin,max}}&=&h \cdot \nu - W_A &\quad \scriptsize \mid\; \nu = \frac{c}{\lambda}\\[5pt] &=&h \cdot \frac{c}{\lambda} - W_A &\quad \scriptsize \\[5pt] &=& \left(h\cdot c \right)\cdot \frac{1}{\lambda} - W_A \end{array}$

Abbildung zum besseren Verständinis

Einzeichnen der Messwerte in ein Koordinatensystem kann die Regressionsgerade durch händisches Ablesen liefern. Alternativ: Eingabe der Messwerte in den Taschenrechner, Anzeige des Graphen und dortiges Ablesen der Regressionsgeraden.

Durch Ablesen der Steigung und des $y$ -Achsenabschnittes ergibt sich die Regressionsgerade. Diese wird im Folgenden wieder in Zusammenhang mit der Gleichung für die Energiebilanz gesetzt.

$y = 1166,81 \;\text{eVnm}\cdot x-1,38 \;\text{eV}$

Rechenweg anzeigen

$\left(h\cdot c \right)\cdot \frac{1}{\lambda} - W_A = 1166.81 \;\text{eVnm}\cdot x-1.38 \;\text{eV}$

Koeffizientenvergleich: Die Steigung der Regressionsgeraden liefert $h\cdot c:$

Rechenweg anzeigen

$h=4 \cdot 10^{-15}\;\text{eVs}$

Der $y$ -Achsenabschnitt der Regressionsgeraden liefert die Austrittsarbeit:

$\begin{array}[t]{rll} W_A &=& 1,4 \;\text{eV} \end{array}$

3.1

Massenspektroskopie: Trennt gleichartige Teilchen unterschiedlicher Masse voneinander.

Nachweis des $\beta ^+$ -Strahlers, also Anwendung auf den Nachweis positiv geladener Elementarteilchen.

Aufbau eines Massenspektrographen:

Teil: Geschwindigkeitsfilter, der aus einem homogemnen elektrischen und magnetischen Feld besteht, wobei sich für eine definierte Geschwindigkeit Lorentz- und elektrische Feldkraft aufheben. Diesen können deswegen nur geladene Teilchen mit identischer Geschwindigkeit durchlaufen.
Teil: magnetisches Ablenkfeld, das aus einem homogenen Magnetfeld besteht, in dem die Teilchen durch die Lorentzkraft auf eine Kreisbahn abgelenkt werden.

Positronen, die emmitiert werden, haben unterschiedliche Geschwindigkeiten, aber eine identische Masse. Dadurch gibt es nur eine Kreisbahn. Auf die Art der Ladung wird aus der Ablenkrichtung geschlossen.

Der Radius der Kreisbahn kann bestimmt und folglich auch die spezifische Ladung berechnet werden. Mit einem Vergleich des Literaturwertes können Alphateilchen ausgeschlossen werden.

3.2

Beim Zerfall des Cu-64-Kerns findet ein $\beta^{+}$ -Zerfall statt.

$^{64}_{29} \text{Cu} \xrightarrow{\beta +}$ $^{64}_{28}\text{Ni} + ^{0}_{1}e^+ + ^{0}_{0}\nu$

3.3

Die Formel für die Aktivität $A$ liefert die Anzahl der Kerne $N\left(t\right)$ zum Zeitpunkt $t:$

Rechenweg anzeigen

$\dfrac{A\left( 0\;\text{s}\right)}{\lambda}= N\left( 0\;\text{s}\right)$

Dabei entspricht $N\left(0\;\text{s}\right)$ der Anzahl der Kerne zu Beginn und $A\left( 0\;\text{s}\right)$ entspricht der Anfangsaktivität.

Für die Zerfallskonstante $\lambda$ gilt:

$\begin{array}[t]{rll} \lambda&=&\dfrac{\ln(2)}{T_{\frac{1}{2}}} &\quad \scriptsize \mid\; T_{\frac{1}{2}}= 12,701 \text{ h}\\[5pt] &=& \dfrac{\ln(2)}{12,701 \text{ h}} &\quad \scriptsize \\[5pt] &=& \dfrac{\ln(2)}{45723,6 \text{ s}} &\quad \scriptsize \\[5pt] &=& 1,52 \cdot 10^{-5}\;\dfrac{1}{\text{s}} \end{array}$

Einsetzen in die Gleichung liefert:

Rechenweg anzeigen

$N\left( 0\;\text{s}\right)=6.6 \cdot 10^{13}$

Das Präperat enthält zu Beginn etwa $7\cdot 10^{13}$ Kerne.

3.4

Für die freiwerdende Energie gilt:

Rechenweg anzeigen

$E=-0,65\;\text{MeV}$

3.5

Gegeben: $m_{\text{Cu-}64}=63,91386 \;\text{u},$ $m_p = 1,007287 \;\text{u},$ $m_n = 1,008665 \;\text{u}$

Gesucht: $E_B/A$

Lösung:

1. Schritt: Massendefekt berechnen

Rechenweg anzeigen

$\Delta m=...$

Da $1 \;\text{u} = 1,660539 \cdot 10^{-27} \;\text{kg}$ folgt:

$\begin{array}[t]{rll} \Delta m&=& -0,600738 \cdot 1,660539 \cdot 10^{-27} \;\text{kg} \\[5pt] &=& -9,975489 \cdot 10^{-28} \;\text{kg} \end{array}$

2. Schritt: Bindungsenergie berechnen

Rechenweg anzeigen

$E_B=...$

3. Schritt: Kernbindungsenergie pro Nukleon berechnen

$\begin{array}[t]{rll} \,\bigg \vert \,\dfrac{E_B}{A} \,\bigg \vert \,&=&\,\bigg \vert \,\dfrac{8,89 \cdot 10^{-11} \;\text{J}}{64} \,\bigg \vert \ \\[5pt] &\approx& 1,4\cdot 10^{-12} \;\text{J} \\[5pt] &=& 8,7 \;\text{MeV} \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?