Teil C – Experimente
Hinweis: Von den nachfolgenden Wahlaufgaben C 1 und C 2 soll in der Prüfung nur eine bearbeitet werden.
Ein Experimentierwagen steht auf einer waagerechten Unterlage. Er ist zwischen zwei gleichen Federn eingespannt und ruht in der Gleichgewichtslage. Wird der Wagen ausgelenkt und freigegeben, so führt er eine harmonische Schwingung aus. Die Abbildung zeigt das Prinzip.
 Plane das Experiment den folgenden Aufgabenstellungen gemäß.
Plane das Experiment den folgenden Aufgabenstellungen gemäß.
Die vollständig aufgebaute Experimentieranordnung sowie alle erforderlichen Geräte und Hilfsmittel werden Ihnen übergeben. Das planvolle und systematische Experimentieren wird bewertet.
Wahlaufgabe C 1: Spule und Kondensator im Gleich- und Wechselstromkreis
Führe Untersuchungen an einer Spule und an einer Reihenschaltung aus Spule und Kondensator durch. Plane das Experiment den folgenden Aufgabenstellungen gemäß und fordere bei der Aufsicht führenden Fachlehrkraft die notwendigen Geräte und Hilfsmittel an. Das vollständige Anfordern aller notwendigen Geräte und Hilfsmittel sowie das planvolle und systematische Experimentieren werden bewertet.
Erreichbare BE-Anzahl: 02
1
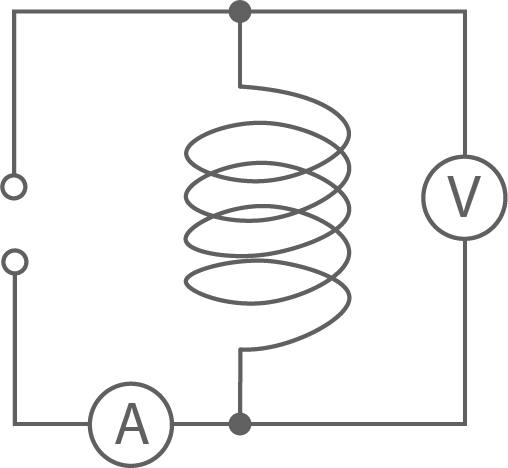
Ermittle für die vorgegebene Spule durch Strom- und Spannungsmessung den Ohm'schen Widerstand  Erfrage bei der Aufsicht führenden Fachlehrkraft, welche Gleichspannung nicht überschritten werden darf.
Erfrage bei der Aufsicht führenden Fachlehrkraft, welche Gleichspannung nicht überschritten werden darf.
Erreichbare BE-Anzahl: 03
2
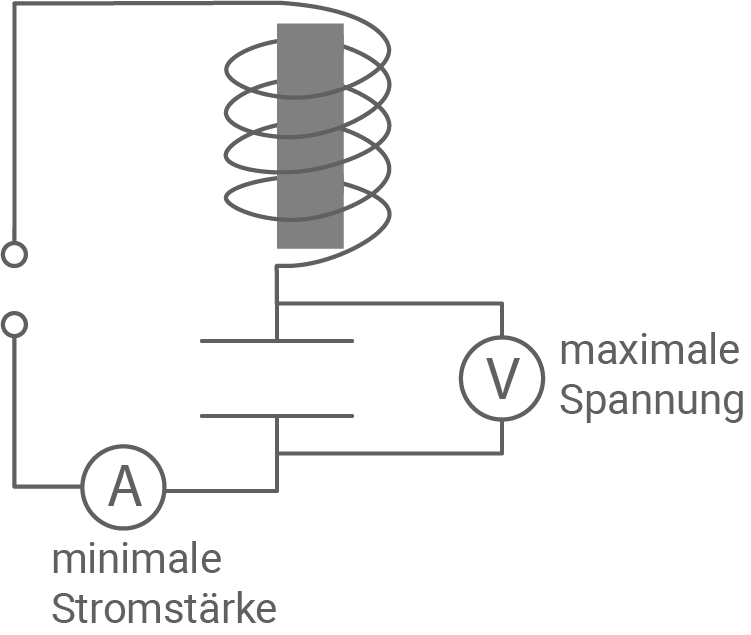
Baue eine Reihenschaltung aus einer Spule mit Eisenkern und einem Kondensator auf. Die Stromstärke und die über dem Kondensator abfallende Spannung sollen gemessen werden.
Erfrage bei der Aufsicht führenden Fachlehrkraft die Einstellung der Wechselspannungsquelle und die Frequenz der Wechselspannung.
Durch Verschieben des Eisenkerns wird die Induktivität der Spule verändert. Verschiebe den Eisenkern so, dass es zur Reihenresonanz kommt.
2.1
Messe für diesen Fall den Effektivwert der Stromstärke und den Effektivwert der über dem Kondensator abfallenden Spannung.
Erreichbare BE-Anzahl: 01
2.2
Berechne unter Nutzung der Messwerte aus Teilaufgabe 2.1 den kapazitiven Widerstand  des Kondensators.
des Kondensators.
Erreichbare BE-Anzahl: 02
2.3
Der Wert des kapazitiven Widerstands ist fehlerbehaftet. Erfrage bei der Aufsicht führenden Fachlehrkraft die absoluten Messunsicherheiten für die Stromstärke und die Spannung.
Ermittle den absoluten und den relativen Fehler des kapazitiven Widerstands.
Erreichbare BE-Anzahl: 03
2.4
Gib den induktiven Widerstand  der Spule und den Gesamtwiderstand der Schaltung an.
der Spule und den Gesamtwiderstand der Schaltung an.
Erreichbare BE-Anzahl: 02
2.5
Zeichne ein zugehöriges Zeigerdiagramm ausschließlich für die Spule.
Erreichbare BE-Anzahl: 02
Wahlaufgabe C 2: Mechanische Schwingungen
Führe Untersuchungen an einem schwingungsfähigen System durch.Ein Experimentierwagen steht auf einer waagerechten Unterlage. Er ist zwischen zwei gleichen Federn eingespannt und ruht in der Gleichgewichtslage. Wird der Wagen ausgelenkt und freigegeben, so führt er eine harmonische Schwingung aus. Die Abbildung zeigt das Prinzip.

Die vollständig aufgebaute Experimentieranordnung sowie alle erforderlichen Geräte und Hilfsmittel werden Ihnen übergeben. Das planvolle und systematische Experimentieren wird bewertet.
Erreichbare BE-Anzahl: 01
1
Löse eine der beiden Federn aus der Experimentieranordnung und ermittle experimentell deren Federkonstante 
Erreichbare BE-Anzahl: 03
2
Stelle den ursprünglichen Zustand der Experimentieranordnung her. Lenke den Wagen aus der Gleichgewichtslage aus und gib ihn frei.
2.1
Messe die Periodendauer des schwingungsfähigen Systems.
Erreichbare BE-Anzahl: 02
2.2
Erfrage die Masse des Wagens bei der Aufsicht führenden Fachlehrkraft. Berechne die Richtgröße  des schwingungsähigen Systems.
des schwingungsähigen Systems.
Erreichbare BE-Anzahl: 02
3
Gib das Verhältnis  zu
zu  an.
an.
Erreichbare BE-Anzahl:01
4
Bei einem anderen schwingungsfähigen System gleicher Bauart beträgt die Richtgröße  . Der Wagen hat die Gesamtmasse
. Der Wagen hat die Gesamtmasse  . Die Auslenkung
. Die Auslenkung  wird in Abhängigkeit von der Zeit
wird in Abhängigkeit von der Zeit  gemessen.
Die Abbildung zeigt das zugehörige
gemessen.
Die Abbildung zeigt das zugehörige  -Diagramm.
-Diagramm.
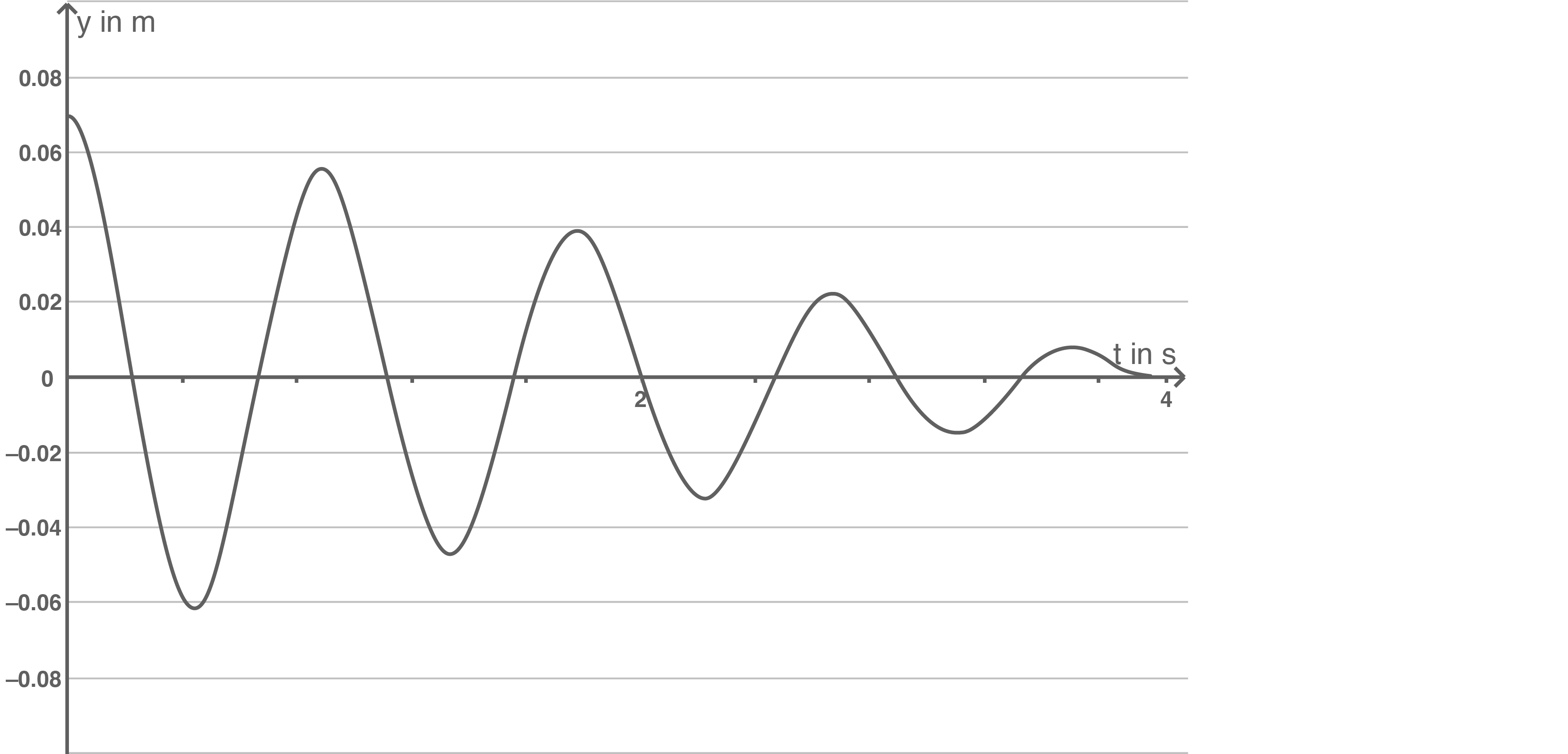 Die Spannenergie wird durch Reibungsarbeit vollständig entwertet. Die Reibungskraft ist konstant.
Die Spannenergie wird durch Reibungsarbeit vollständig entwertet. Die Reibungskraft ist konstant.

4.1
Gib die Periodendauer an.
Erreichbare BE-Anzahl: 01
4.2
Ermittle den insgesamt vom Wagen zurückgelegten Weg  .
.
Erreichbare BE-Anzahl: 02
4.3
Berechne die Reibungszahl  .
.
Erreichbare BE-Anzahl: 03
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
C1
1.
2.1
2.2
Der kapazitive Widerstand  ist in Wechselstromschaltungen definiert als:
ist in Wechselstromschaltungen definiert als:
![\(\begin{array}[t]{rll}
X_{\text{C}}&=& \dfrac{U_{\text{eff}}}{I_{\text{eff}}}
\end{array}\)](https://www.schullv.de/resources/formulas/3d41ddd79e34e926f50ee92f17a3b16d5fbc2c2857d5ccaefeb54a8497ec42bc_light.svg) Einsetzen der gemessenen Werte liefert:
Einsetzen der gemessenen Werte liefert:
![\(\begin{array}[t]{rll}
X_{\text{C}}&=& \dfrac{U_{\text{eff}}}{I_{\text{eff}}} &\quad \scriptsize \\[5pt]
&=& \dfrac{6 \; \text{V}}{0.8 \;\text{A}} &\quad \scriptsize \\[5pt]
&=& 7,5 \; \Omega
\end{array}\)](https://www.schullv.de/resources/formulas/b1a89fb8fa906b873f578fb35ebac44625ef776eb4d1a9767f907294073769d3_light.svg)
2.3
Beispielsweise  und
und  entsprechen jeweils der absoluten Messunsicherheit der Stromstärke und der Spannung.
Für den abosluten Fehler des kapazitiven Widerstandes
entsprechen jeweils der absoluten Messunsicherheit der Stromstärke und der Spannung.
Für den abosluten Fehler des kapazitiven Widerstandes  gilt:
Für den relativen Fehler des kapazitiven Widerstandes
gilt:
Für den relativen Fehler des kapazitiven Widerstandes  gilt:
gilt:
![\(\begin{array}[t]{rll}
\dfrac{\Delta X_{\text{C}}}{X_{\text{C}}}&=&\dfrac{ 1,13 \;\Omega}{7,5 \;\Omega} &\quad \scriptsize \\[5pt]
&=& 0,15 &\quad \scriptsize \\[5pt]
&=& 15 \;\%
\end{array}\)](https://www.schullv.de/resources/formulas/40dd7770312a47030b742fbe1b51d354eea3621b378d069d16f9344b3da1117e_light.svg)
2.4
Induktiver Widerstand der Spule  enstpricht im Reihenresonanzfall dem kapazitiven Widerstand
enstpricht im Reihenresonanzfall dem kapazitiven Widerstand  Der Betrag ist gleich.
Der Betrag ist gleich.
![\(\begin{array}[t]{rll}
X_{\text{L}}&=& X_{\text{C}}&\quad \scriptsize \\[5pt]
&=& 7,5 \; \Omega
\end{array}\)](https://www.schullv.de/resources/formulas/a2e0fa9ba33451c236a261dc9f34db7de7e642773952cc0e5ede202d8dcc689b_light.svg) Für den Gesamtwiderstand im Reihenresonanzfall
Für den Gesamtwiderstand im Reihenresonanzfall  gilt:
gilt:
![\(\begin{array}[t]{rll}
R_{\text{ges}}&=& X_{\text{L}}+X_{\text{C}} &\quad \scriptsize \mid\; X_{\text{L}}=-X_{\text{C}}\\[5pt]
&=& X_{\text{C}}- X_{\text{C}} &\quad \scriptsize \\[5pt]
&=& 0 \; \Omega
\end{array}\)](https://www.schullv.de/resources/formulas/eeaddcd2559fd34d7ccc3a76835bc58f472ead58fa57e023c6e7fa28babab356_light.svg)
2.5
Zeigerdiagramm
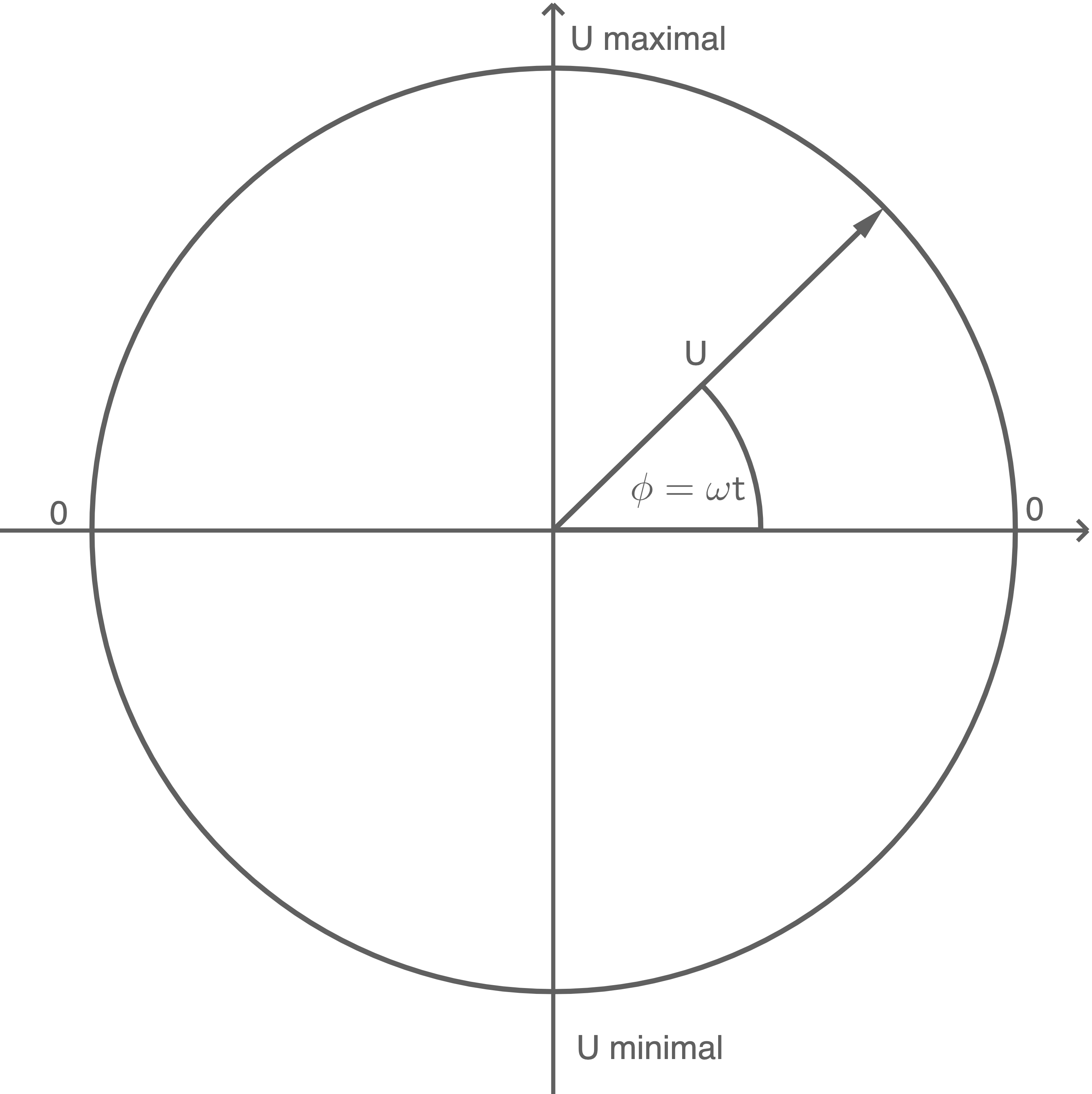

C2
1.
Die Federkonstante  kann mit Hilfe folgender Formel berechnet werden:
kann mit Hilfe folgender Formel berechnet werden:
![\(\begin{array}[t]{rll}
T&=& 2 \pi\cdot \sqrt{\dfrac{m}{D_{\text{Feder}}}} &\quad \scriptsize \mid\; \left(\;\right)^2\\[5pt]
T^2&=& 4\pi^2\cdot \dfrac{m}{D_{\text{Feder}}} &\quad \scriptsize \mid\; \cdot D_{\text{Feder}}\\[5pt]
T^2\cdot D_{\text{Feder}}&=& 4\pi^2\cdot m &\quad \scriptsize \mid\;\cdot \dfrac{1}{T^2} \\[5pt]
D_{\text{Feder}}&=& \dfrac{4\pi^2\cdot m}{T^2}
\end{array}\)](https://www.schullv.de/resources/formulas/cbaed940e3a55b8f5af8764b06154c571945adc21048d9833845ac8e0e26bcb9_light.svg) Zur Bestimmung der Periodendauer
Zur Bestimmung der Periodendauer  kann eine Masse
kann eine Masse  am unteren Ende der Feder befestigt und losgelassen werden, sodass sie zu schwingen beginnt. Mit Hilfe einer Stoppuhr wird die Zeit gemessen, die die Masse für eine vollständige Schwingung benötigt. Dabei wird die Zeit von dem Moment gemessen, wenn die Masse ihre maximale Auslenkung erreicht hat, bis zu dem Zeitpunkt, wenn sie wieder dieselbe maximale Auslenkung in der gleichen Richtung erreicht. Beispielsweise liefert eine gemessene Periodendauer von
am unteren Ende der Feder befestigt und losgelassen werden, sodass sie zu schwingen beginnt. Mit Hilfe einer Stoppuhr wird die Zeit gemessen, die die Masse für eine vollständige Schwingung benötigt. Dabei wird die Zeit von dem Moment gemessen, wenn die Masse ihre maximale Auslenkung erreicht hat, bis zu dem Zeitpunkt, wenn sie wieder dieselbe maximale Auslenkung in der gleichen Richtung erreicht. Beispielsweise liefert eine gemessene Periodendauer von  für eine Masse
für eine Masse 
![\(\begin{array}[t]{rll}
D_{\text{Feder}}&=& \dfrac{4\pi^2\cdot m}{T^2}&\quad \scriptsize \\[5pt]
&=& \dfrac{4\pi^2\cdot 0,30 \;\text{kg}}{\left(1,66\;\text{s}\right)^2}&\quad \scriptsize \\[5pt]
&=& 4,3 \; \dfrac{\text{N}}{\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/52cba552ba3420be7221b1b3323e46ddf650de36fbc9389d9c086f1512aa92ce_light.svg)
2.1
Mit Hilfe einer Stoppuhr wird die Zeit gemessen, die der Wagen für eine vollständige Schwingung benötigt, also von der maximalen Auslenkung zur maximalen Auslenkung in derselben Richtung.Mehrfache Wiederholungen und die Berechnung des Mittelwerts der gemessenen Periodendauern  liefern genauere Ergebnisse. Beispielsweise ergibt das Experiment:
liefern genauere Ergebnisse. Beispielsweise ergibt das Experiment:
Der Mittelwert der Periodendauern liefert:
| Messung | |
|---|---|
| 1 | 1,00 |
| 2 | 0,96 |
| 3 | 0,92 |
| 4 | 0,98 |
| 5 | 0,94 |
2.2
Die Masse des Wagens wiegt beispielsweise  Für die Priodendauer des Systems gilt:
Für die Priodendauer des Systems gilt:
![\(\begin{array}[t]{rll}
T&=& 2 \pi\cdot \sqrt{\dfrac{m}{D_s}} &\quad \scriptsize \mid\; \left(\;\right)^2\\[5pt]
T^2&=& 4\pi^2\cdot \dfrac{m}{D_s} &\quad \scriptsize \mid\; \cdot D_s\\[5pt]
T^2\cdot D_s&=& 4\pi^2\cdot m &\quad \scriptsize \mid\;\cdot \dfrac{1}{T^2} \\[5pt]
D_s&=& \dfrac{4\pi^2\cdot m}{T^2}
\end{array}\)](https://www.schullv.de/resources/formulas/4674270ae73951adec9d9b730ce8a70be7a8afb22f23e9e956b2a5ed83729e9d_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
D_s&=& \dfrac{4\pi^2\cdot m}{T^2} &\quad \scriptsize \\[5pt]
&=& \dfrac{4\pi^2\cdot0,2 \, \text{kg}}{\left(0,96\;\text{s}\right)^2} &\quad \scriptsize \\[5pt]
&=& 8,6 \; \dfrac{\text{N}}{\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/4ab9a659a84e26102adbb810435f2a93464bd116a9ca7fe14bb18576d411c7cd_light.svg)
3.
4.1
Die Periodendauer entspricht einer vollständigen Schwingung des Wagens, also beispielsweise der Zeit zwischen zwei Hochpunkten des Graphen. Innerhalb von  hat der Wagen
hat der Wagen  Perioden zurückgelegt. Für die Periodendauer ergibt sich:
Perioden zurückgelegt. Für die Periodendauer ergibt sich:
![\(\begin{array}[t]{rll}
T&=& \dfrac{2 \; \text{s}}{2,25}&\quad \scriptsize \\[5pt]
&=& 0,89 \; \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/8b96a1c780c1e66f316512cdbfd6382053b6290b1c16916a59515c5033cceaa5_light.svg) Alternativ lässt sich die Periodendauer mit den Angaben auch berechnen:
Alternativ lässt sich die Periodendauer mit den Angaben auch berechnen:
![\(\begin{array}[t]{rll}
T&=& 2\pi\cdot \sqrt{\dfrac{m}{D_s}} &\quad \scriptsize \\[5pt]
&=& 2\pi\cdot \sqrt{\dfrac{0,10 \; \text{kg}}{5,1 \dfrac{\text{N}}{\text{m}}}} &\quad \scriptsize \\[5pt]
&=& 0,88 \; \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/70f227030f9ac0a2d8c8ca9933315d984a9547c0b467f25b00ce14391323436a_light.svg)
4.2
Aufaddieren der Beträge der Extrempunkte des Graphen liefert den insgesamt vom Wagen zurückgelegt Weg 
4.3
Für die Reibungszahl  gilt:
gilt:
![\(\begin{array}[t]{rll}
\beta &=& \dfrac{\mu}{2\cdot m} &\quad \scriptsize \mid\; \cdot2\cdot m \\[5pt]
\beta \cdot 2\cdot m &=&\mu
\end{array}\)](https://www.schullv.de/resources/formulas/2a8977aff6f5e0d6c09d64d36389e401600807f25d5db101e8e0e88a5f3ced8a_light.svg)
 lässt sich über die Bewegungsgleichung eines harmonischen gedämpften Oszillators berechnen. An einem Maximum gilt:
lässt sich über die Bewegungsgleichung eines harmonischen gedämpften Oszillators berechnen. An einem Maximum gilt:
![\(\begin{array}[t]{rll}
y\left(t\right)&=& A e^{-\beta\cdot t}&\quad \scriptsize \mid\; \cdot \dfrac{1}{A} \\[5pt]
\dfrac{y\left(t\right)}{A}&=& e^{-\beta\cdot t}&\quad \scriptsize \mid\; \ln\left(\;\right)\\[5pt]
\ln\left(\dfrac{y\left(t\right)}{A}\right)&=& \ln\left(e^{-\beta\cdot t}\right) &\quad \scriptsize \\[5pt]
\ln\left(\dfrac{y\left(t\right)}{A}\right)&=& -\beta\cdot t &\quad \scriptsize \mid\; \cdot \dfrac{1}{-t}\\[5pt]
\dfrac{\ln\left(\dfrac{y\left(t\right)}{A}\right)}{-t}&=& \beta
\end{array}\)](https://www.schullv.de/resources/formulas/ab8e325193e8d368b212a2a9fb16b35a2c842064b2c0fbd5ecc173ca19a12b81_light.svg) Einsetzen der Werte für das zweite Maximum liefert:
Einsetzen der Werte für das zweite Maximum liefert:
![\(\begin{array}[t]{rll}
\beta &=& \dfrac{\ln\left(\dfrac{y\left(t\right)}{A}\right)}{-t} &\quad \scriptsize \\[5pt]
&=& \dfrac{\ln\left(\dfrac{0,05 \; \text{m}}{0,07 \; \text{m}}\right)}{-0,8 \;\text{s}} &\quad \scriptsize \\[5pt]
&=& 0,42 \; \dfrac{1}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/0b82b8489bc74d9ddb1c52e7a2467f47e975b34517360969f7f0c9699c63cee6_light.svg) Einsetzen in die Gleichung liefert für die Reibungszahl
Einsetzen in die Gleichung liefert für die Reibungszahl 
![\(\begin{array}[t]{rll}
\mu&=&\beta \cdot 2\cdot m &\quad \scriptsize \\[5pt]
&=& 0,42 \; \dfrac{1}{\text{s}} \cdot 2\cdot 0,10 \; \text{kg}&\quad \scriptsize \\[5pt]
&=& 0,08 \; \dfrac{\text{kg}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/80398f6be73dac55b541509ba1fbdd341296c6631db3bf829b483e8675573dc6_light.svg)