Aufstellen von Funktionsgleichungen
Ist eine Parabel gegeben, die durch eine Funktionsgleichung in der Form 
beschrieben werden kann, so kann die Funktionsgleichung rechnerisch bestimmt werden, wenn die Koordinaten zweier Punkte auf dem Graphen der Parabel bekannt sind.
Dabei gibt es drei Möglichkeiten:
und 
Einsetzen von 
in 
![\(\begin{array}[t]{rll}
8&=&9+(-11)\cdot 3+c \\[5pt]
8&=&-24+c \qquad \scriptsize \mid\;+24 \\[5pt]
32&=&c\\[5pt]
c&=&32
\end{array}\)](https://www.schullv.de/resources/formulas/ff865e2dec841138ceed9e7c6234fb8902f863e9ccd3e20d9c19cae950f1b46f_light.svg)
Die Funktionsgleichung lautet demnach 
-Koordinate haben, so kann man den Scheitelpunkt mit folgendem Verfahren bestimmen und erhält damit die Funktionsgleichung.
beschrieben werden kann, so kann die Funktionsgleichung rechnerisch bestimmt werden, wenn die Koordinaten zweier Punkte auf dem Graphen der Parabel bekannt sind.
Dabei gibt es drei Möglichkeiten:
- Wenn einer der Punkte auf der -Achse liegt, kann der Koeffizient
direkt bestimmt werden und mit dem anderen Punkt der Koeffizient 
- Lineares Gleichungssystem aufstellen.
- Schaubild der verschobenen Normalparabel betrachten.
Beispiele
Funktionsterm aufstellen mit einem linearen Gleichungssystem
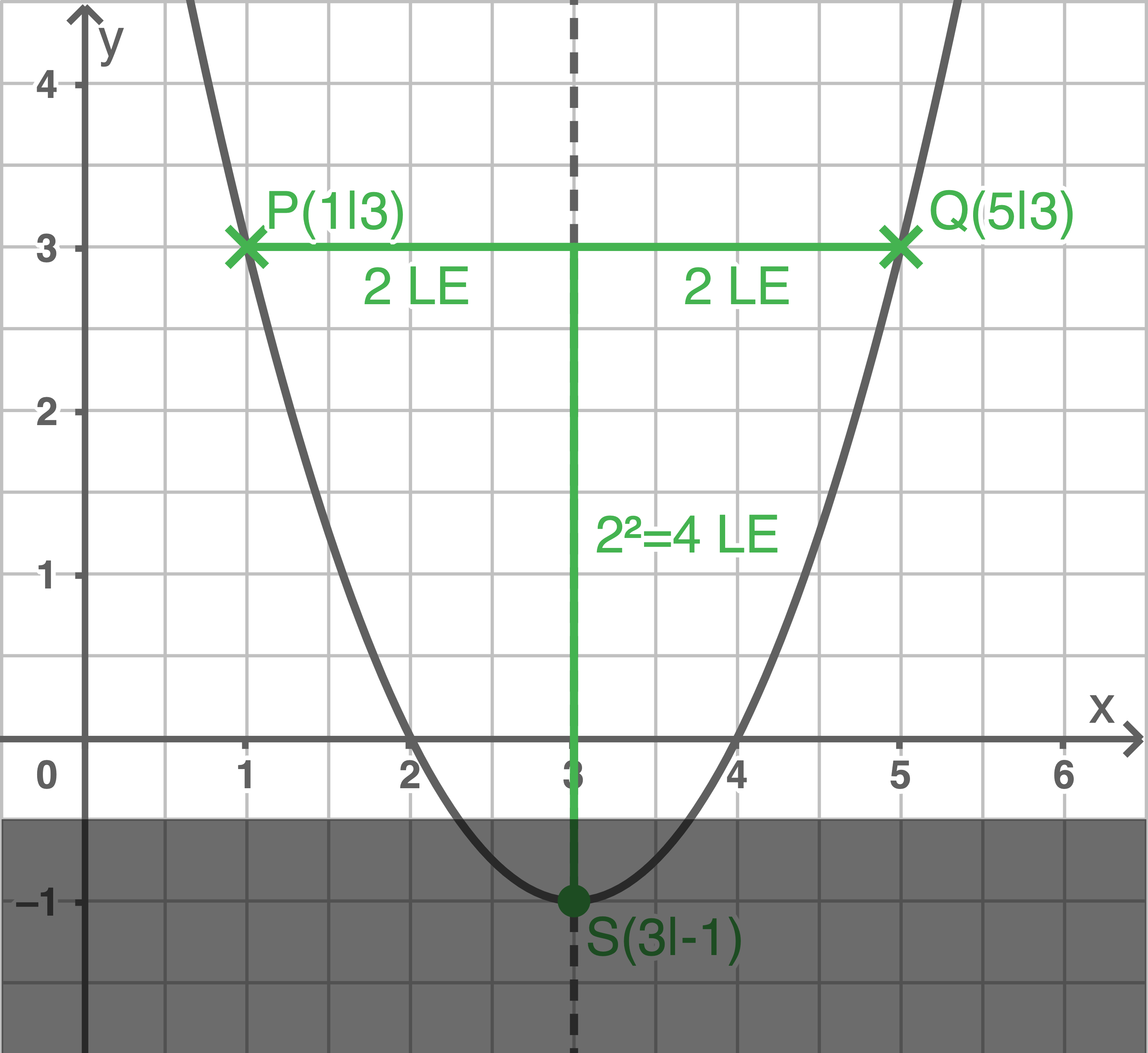
Auf einer verschobenen Normalparabel liegen die Punkte und
Einsetzen von in
Die Funktionsgleichung lautet demnach
Funktionsterm aufstellen durch Betrachtung der verschobenen Normalparabel
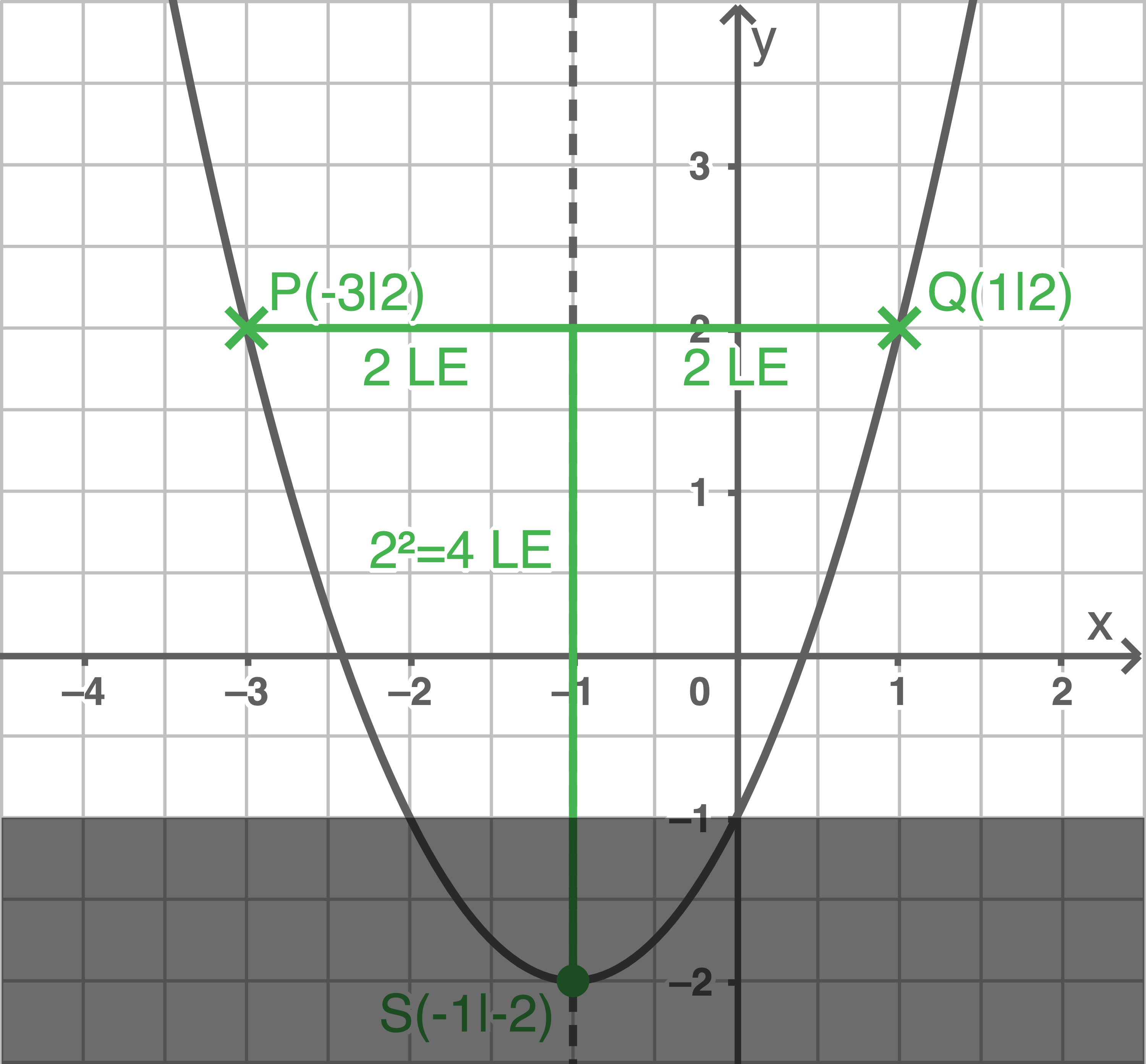
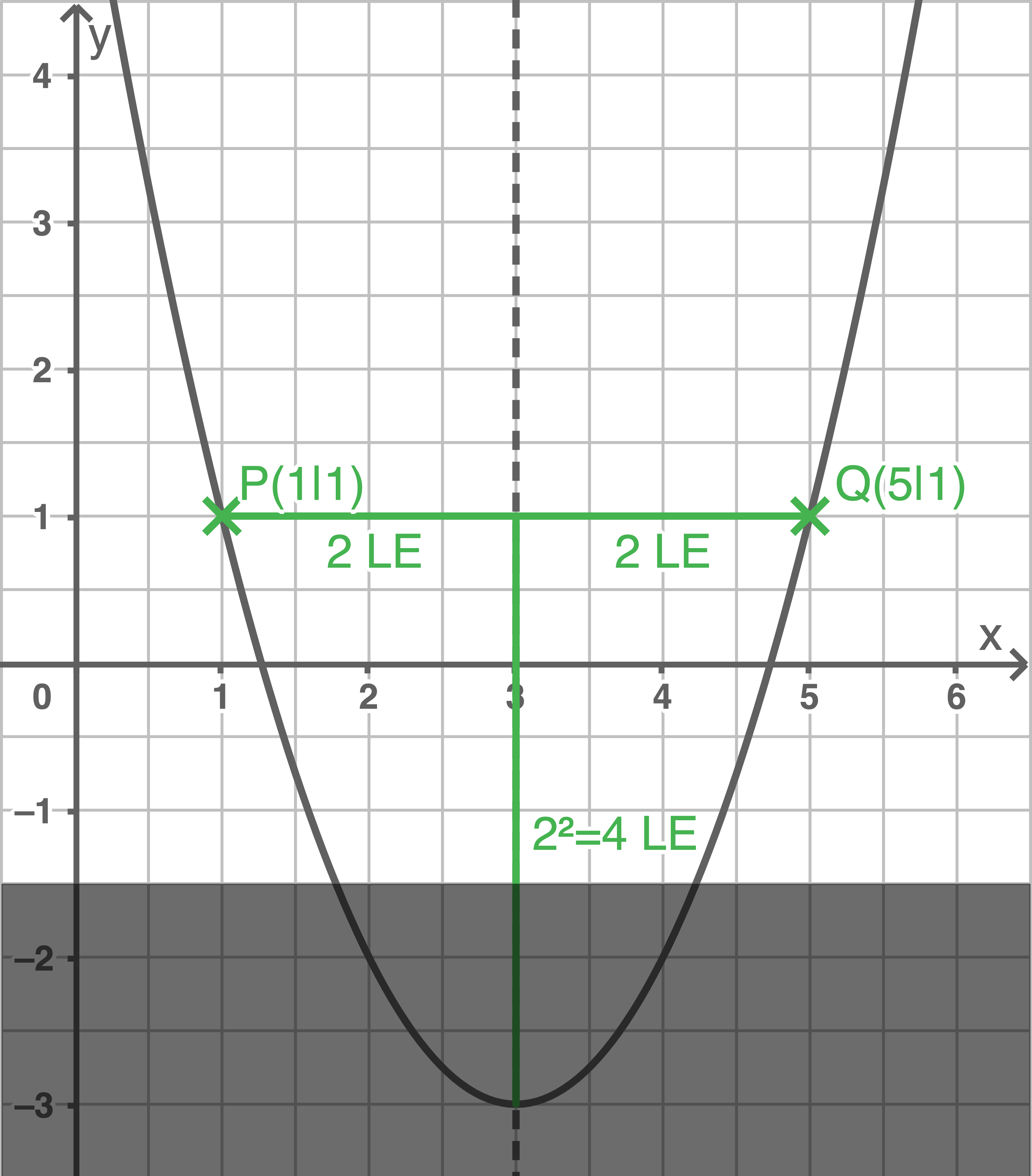
Sind zwei Punkte gegeben, welche die gleiche-Koordinate haben, so kann man den Scheitelpunkt mit folgendem Verfahren bestimmen und erhält damit die Funktionsgleichung.
Der Abstand der Punkte zur Symmetrieachse beträgt 2 LE.
Der Scheitelpunkt 
der Parabel liegt 
unterhalb der Punkte 
und 
Somit hat die Koordinaten 
da die -Koordinate von und 
gleich 1 ist.
Daraus folgt die Funktionsgleichung 
der Parabel liegt unterhalb der Punkte und Somit hat die Koordinaten da die -Koordinate von und gleich 1 ist.
Daraus folgt die Funktionsgleichung
1
Berechne die Koeffizienten 
und der Parabel mit der Funktionsgleichung 
auf der die Punkte und liegen.
, 
, 
und der Parabel mit der Funktionsgleichung auf der die Punkte und liegen.
a)
,
b)
,
2
Bestimme die Funktionsgleichung der verschobenen Normalparabel.
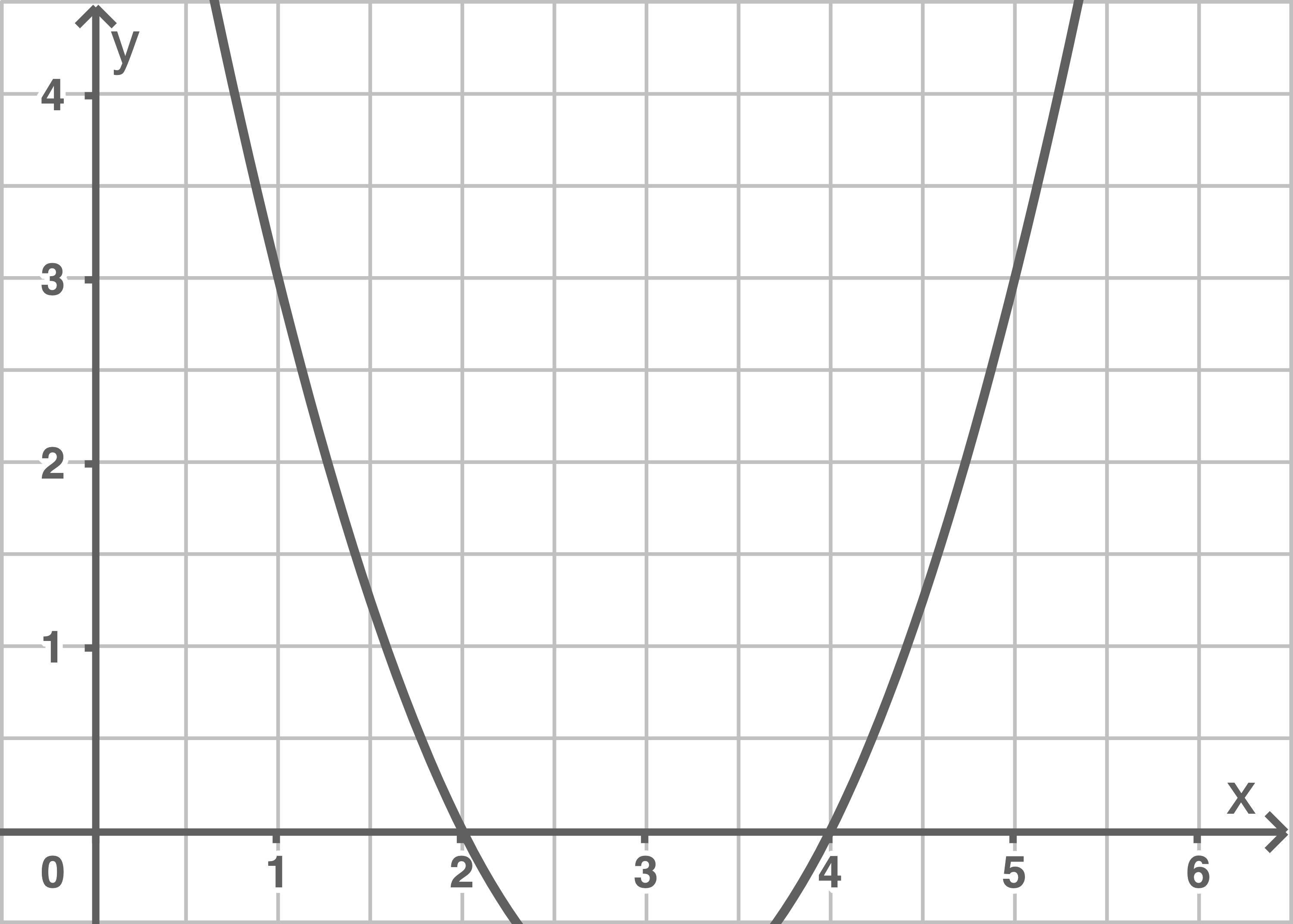
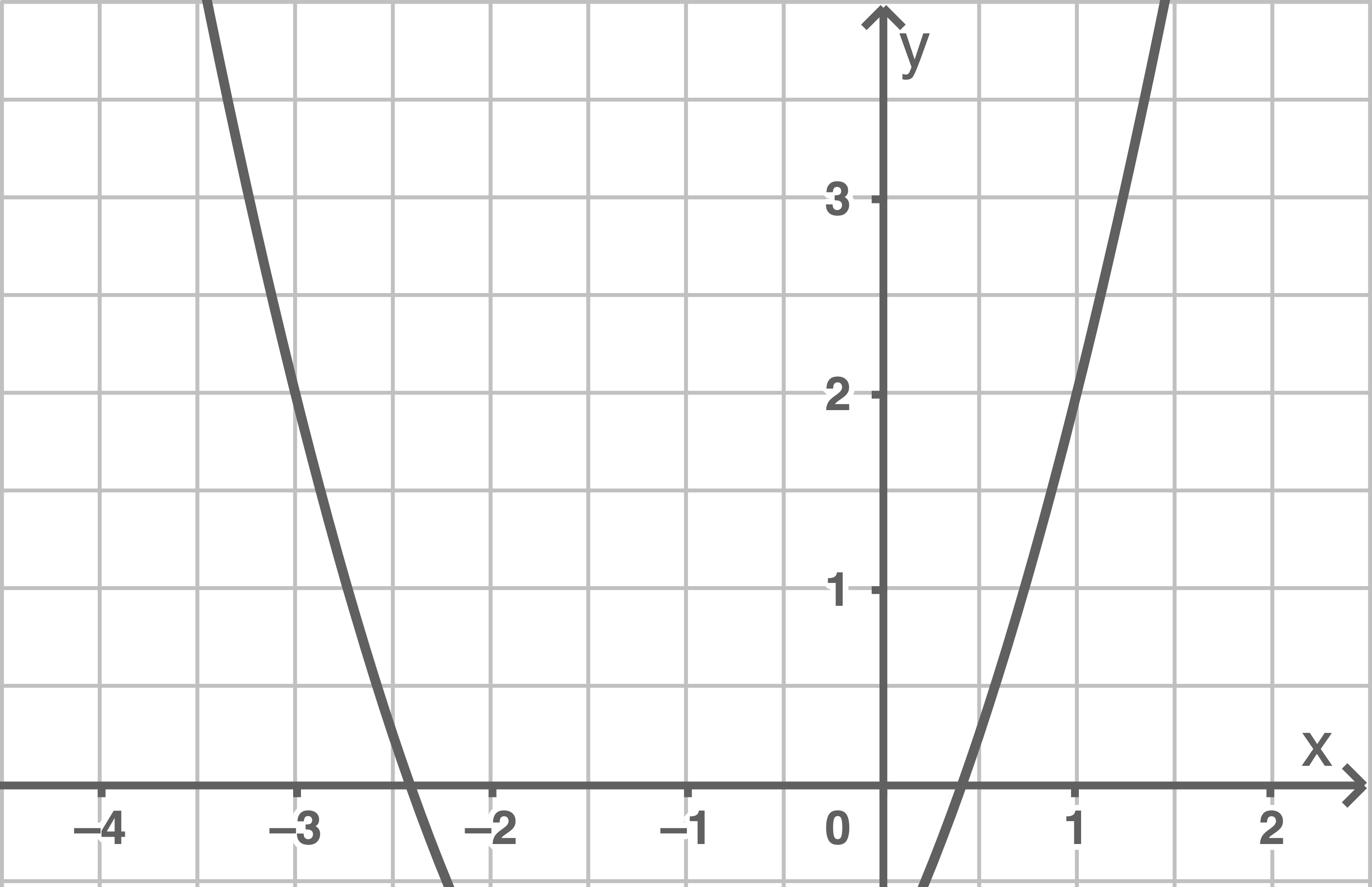
a)
b)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
,
![\(\begin{array}[t]{rrll}
\text{(3) in (1)}&-4&=&4+2\cdot (-5)+c \\
&-4&=&-6+c\quad \scriptsize \mid\;+6 \\
&2&=&c\\
&c&=&2
\end{array}\)](https://www.schullv.de/resources/formulas/8677369ce02afe69cd3c87a7d46c56e8b983060b1348e13000a72818d7584ee7_light.svg)
b)
,
![\(\begin{array}[t]{rrll}
\small\text{(3) in (1)}&1&=&9+3\cdot (-10)+c \\
&1&=&-21+c\quad \scriptsize \mid\;+21 \\
&22&=&c\\
&c&=&22
\end{array}\)](https://www.schullv.de/resources/formulas/ac1c6a792ce3ef205bd7e2eb09a8b6e0818501f66aa493f59c90fe6a804886d3_light.svg)
2
a)
b)
