Zweistufiges Zufallsexperiment mit Zurücklegen
Wird ein Zufallsexperiment zweimal durchgeführt, spricht man von einem zweistufigen Zufallsexperiment. Dabei gelten die Pfadregeln (Produkt- und Summenregel).
Beispiele
Auch bei der zweiten Durchführung gilt:
und 
Gleiches gilt für das Glücksrad.
Weiteres Beispiel
Man spricht deswegen von einem zweistufigen Zufallsexperiment mit Zurücklegen.
- Eine Münze wird zweimal geworfen.
- Ein Glücksrad wird zweimal gedreht.
Auch bei der zweiten Durchführung gilt:
und Gleiches gilt für das Glücksrad.
Weiteres Beispiel
- Eine Kugel wird aus einem Gefäß gezogen, die Farbe der Kugel wird notiert, wieder zurückgelegt und anschließend wird ein zweites Mal eine Kugel gezogen.
1
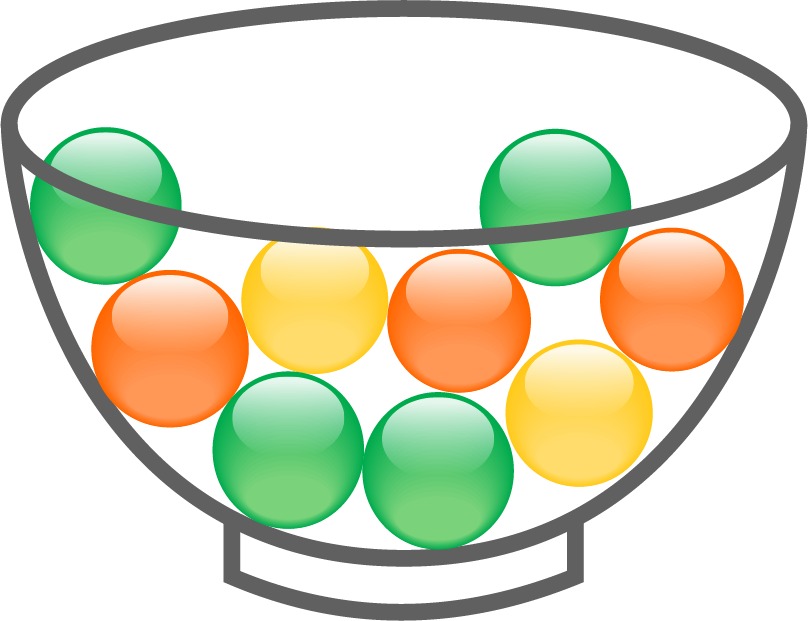
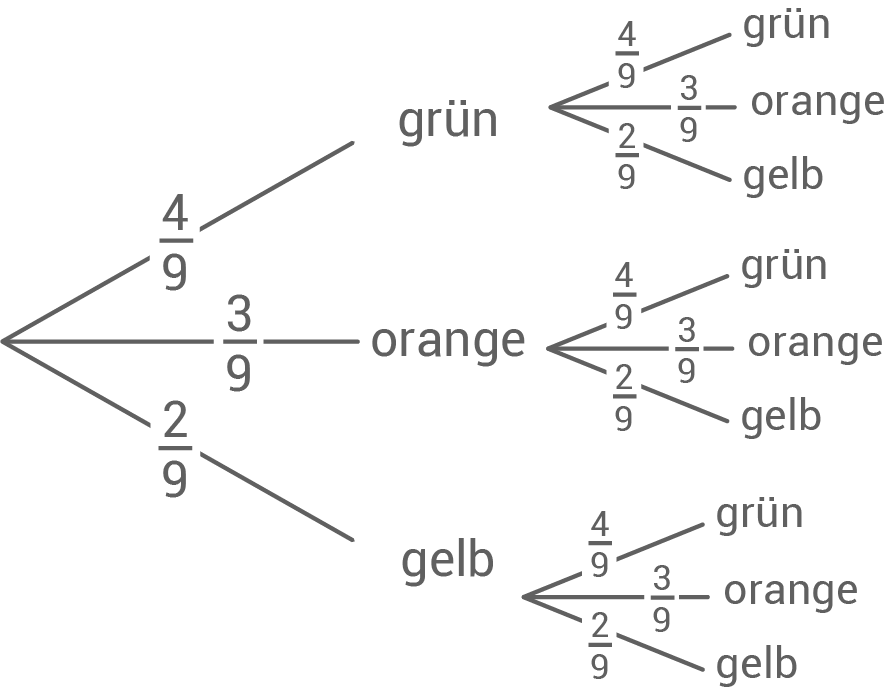
Aus dem nebenstehenden Gefäß zieht Simon eine Kugel, notiert die Farbe der Kugel, legt sie wieder zurück und zieht eine weitere Kugel.
a)
Erstelle für das Zufallsexperiment ein Baumdiagramm.
b)
Wie hoch ist die Wahrscheinlichkeit, dass Simon zwei gelbe Kugeln zieht?
c)
Wie hoch ist die Wahrscheinlichkeit, dass Simon eine orangene und gelbe Kugel zieht?
d)
Wie hoch ist die Wahrscheinlichkeit, dass Simon mindestens eine grüne Kugel zieht?
2
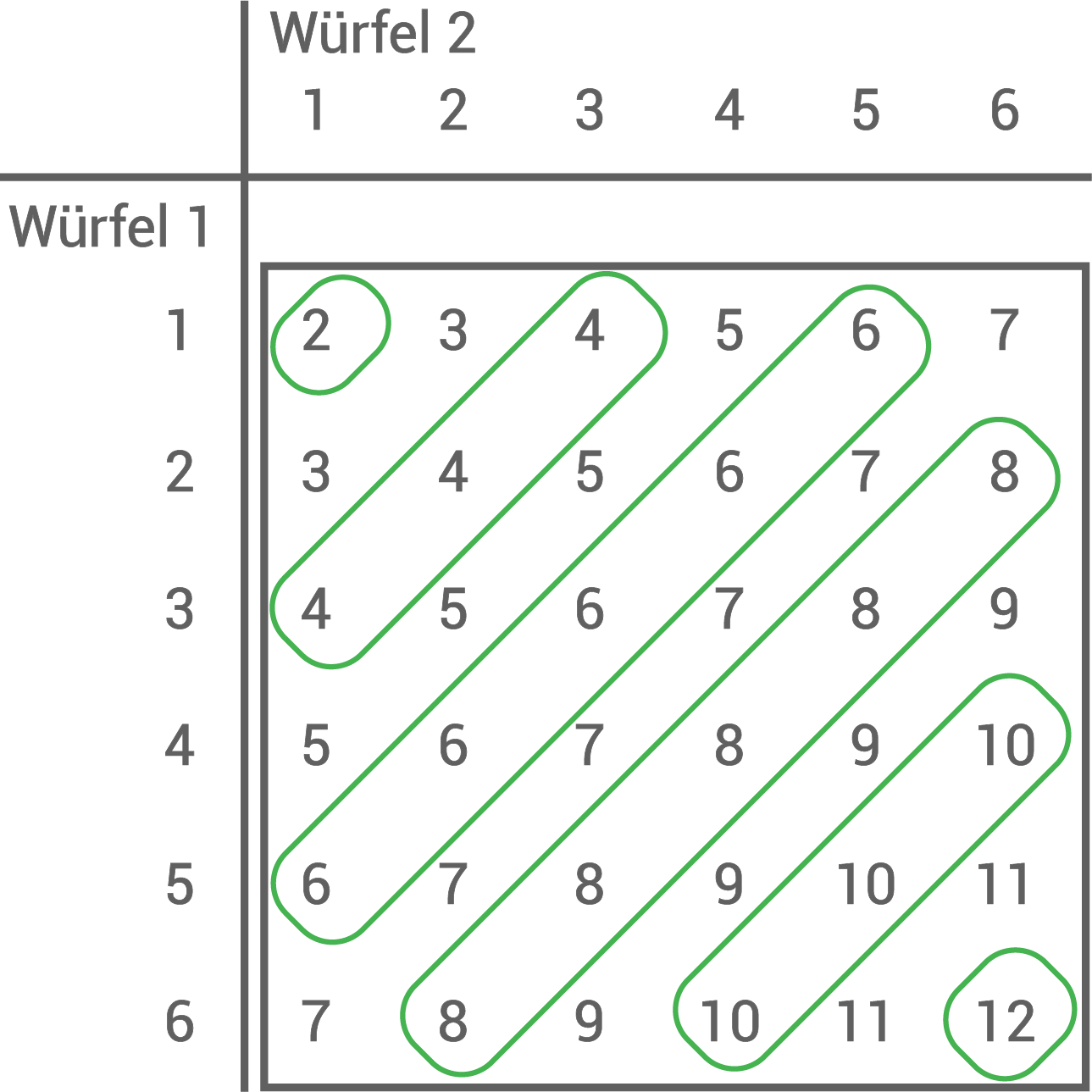
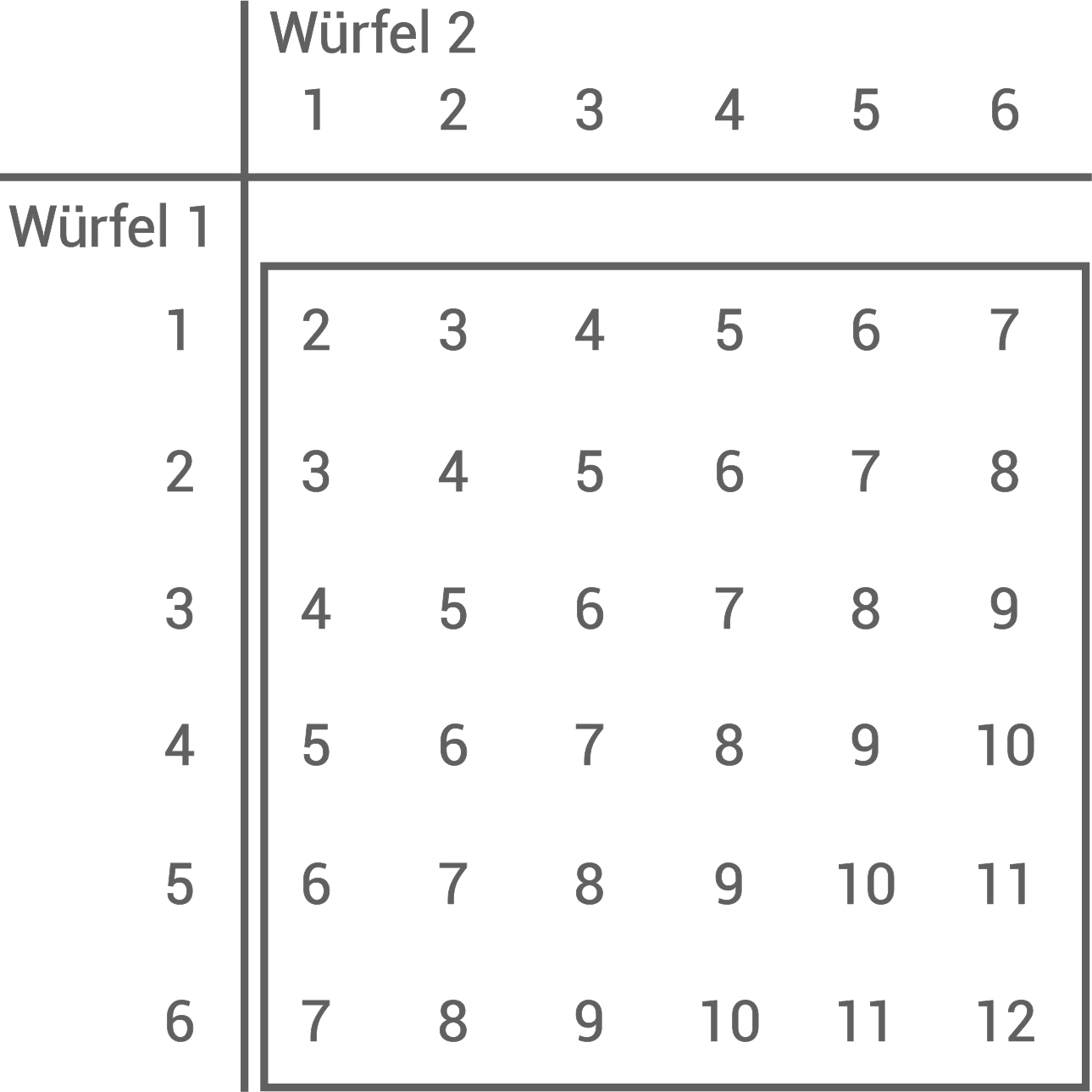
Zwei Würfel werden gleichzeitig geworfen.
a)
Erstelle eine Tabelle mit allen Ergebnissen.
b)
Berechne die Wahrscheinlichkeit, eine 4 und eine 6 zu würfeln.
c)
Berechne die Wahrscheinlichkeit, die Augensumme 10 zu würfeln.
d)
Berechne die Wahrscheinlichkeit, eine gerade Augensumme zu würfeln.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
![\(\begin{array}[t]{rll}
P(\text{gelb, gelb})&=& \dfrac{2}{9}\cdot \dfrac{2}{9} \\[5pt]
&=& \dfrac{4}{81} \\[5pt]
&=& 5\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e36fcb24ba681dd51ff67c9e296411fec9495d1f14aeacf71994a67f9c02eaa2_light.svg)
c)
![\(\begin{array}[t]{rll}
P(\text{orange, gelb})&=& \dfrac{3}{9}\cdot \dfrac{2}{9}+\dfrac{2}{9}\cdot \dfrac{3}{9} \\[5pt]
&=& \dfrac{12}{81} \\[5pt]
&=& 15\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/46620b26452dbd2ae3a0e9066bcd218fcb5c3b179b45ca2aca1eb9750d7a1399_light.svg)
d)
![\(\begin{array}[t]{rll}
&=& 1-P(\overline{\text{grün}}) \\[5pt]
&=& 1-\left(\dfrac{3}{9}\cdot\dfrac{3}{9}+\dfrac{3}{9}\cdot\dfrac{2}{9}+\dfrac{2}{9}\cdot\dfrac{2}{9}+\dfrac{2}{9}\cdot\dfrac{3}{9}\right) \\[5pt]
&=& 1-\left(\dfrac{9}{81}+\dfrac{6}{81}+\dfrac{4}{81}+\dfrac{6}{81}\right) \\[5pt]
&=& 1-\dfrac{25}{81} \\[5pt]
&=& 69\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6d391aab7ac352f69e1bd4164fe0a52a32c17723b28ae0a11721efc2ed710633_light.svg)
2
a)
b)
c)
d)
