Trigonometrie in der Ebene
Berechnungen in Vierecken und auch Vielecken lassen sich durch Unterteilen und Ergänzen durchführen.
Beispiele für passende geometrische Figuren sind Dreiecke, Rechtecke oder Trapeze.
 berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{\text{ABCD}}&=& A_{\text{EBC}}+A_{\text{AECD}}\\[5pt]
&=& 10,8\,\text{cm}^2+26,5\,\text{cm}^2\\[5pt]
A_{\text{ABCD}}&=& 37,3\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/181ea3ebf8ab5ab9ae0689b0793eea6fa8d91c4e6f41e7e12e8340d4af5ffb0b_light.svg)
Beispiel
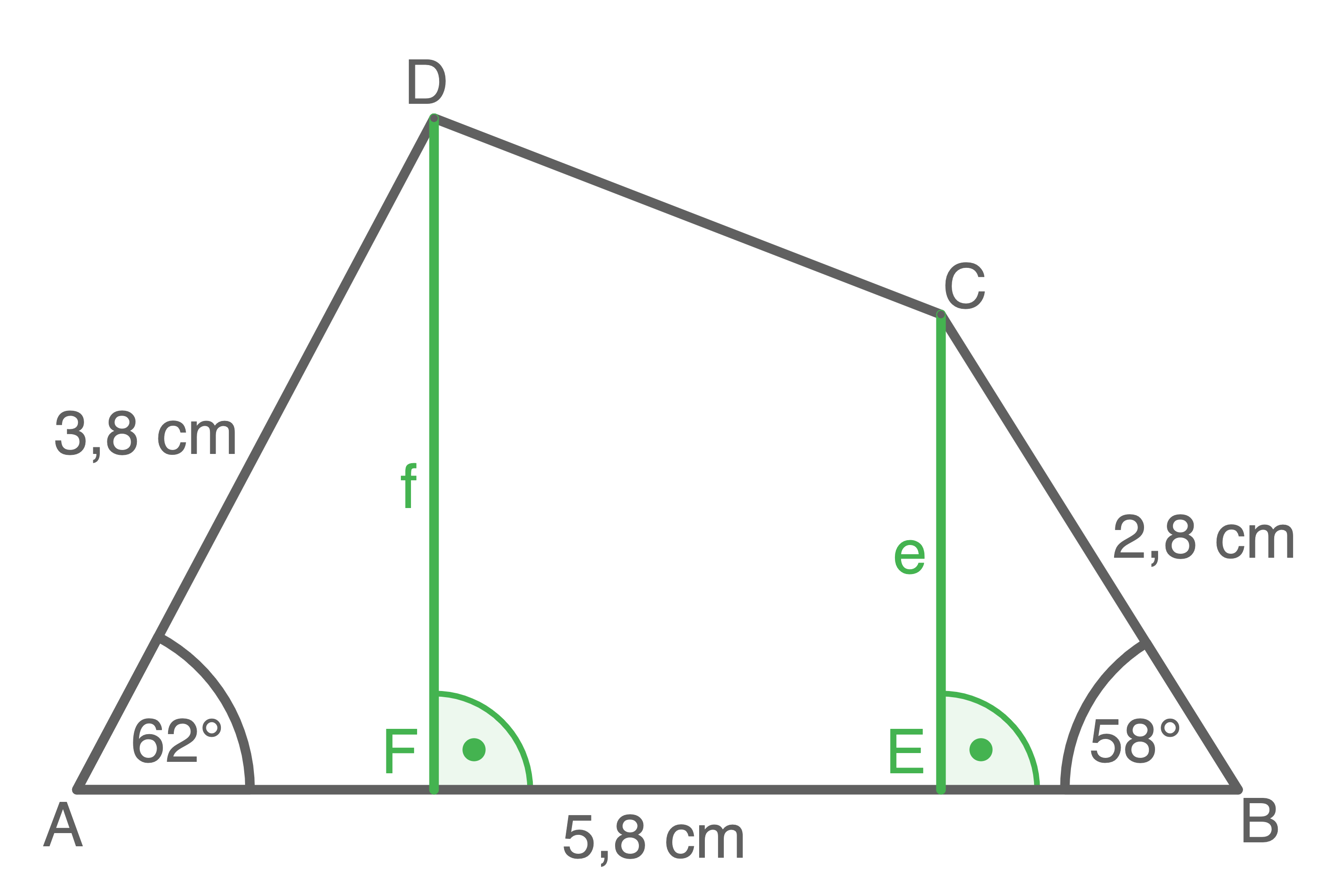
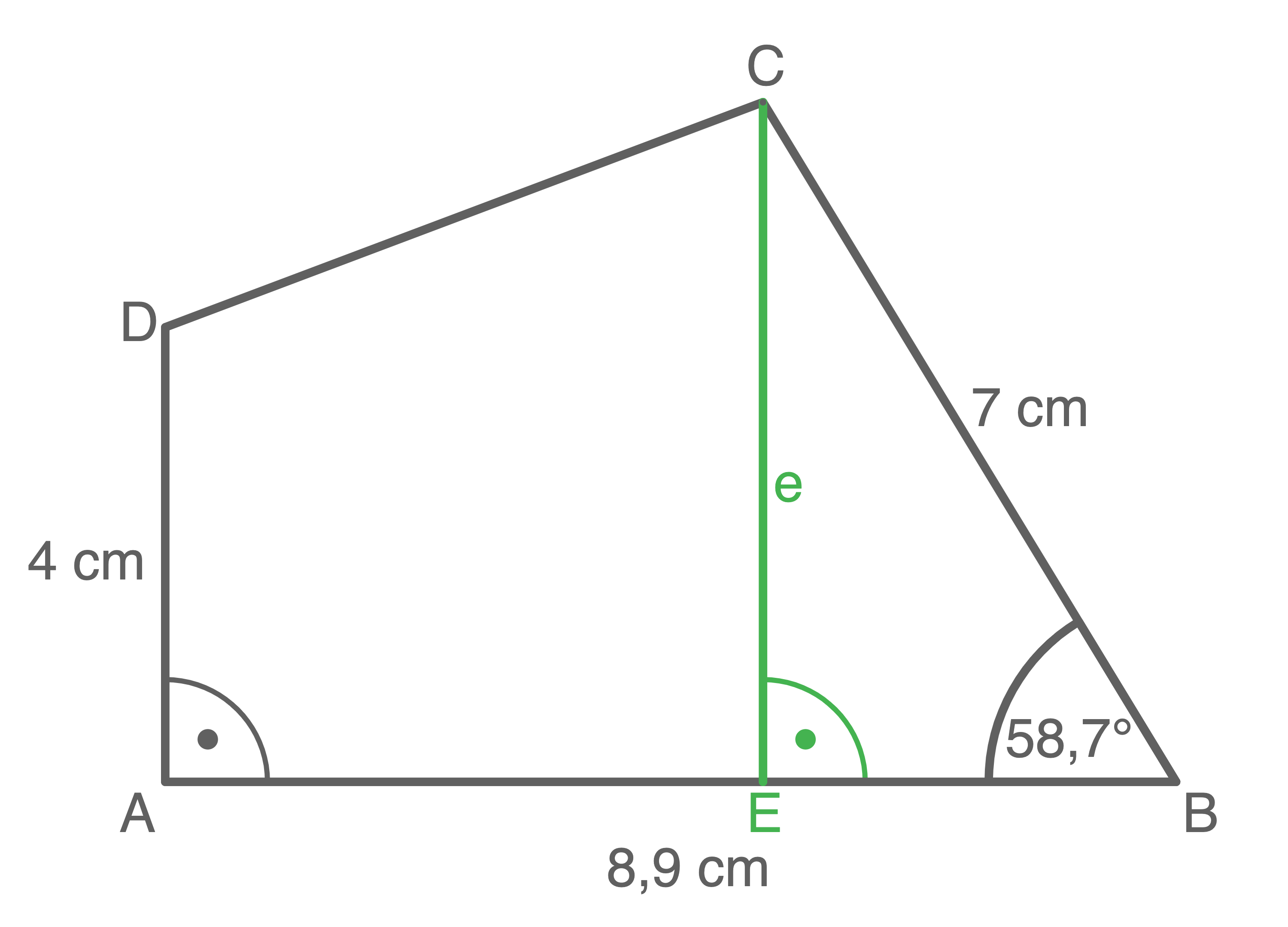
Berechnet werden soll der Flächeninhalt des Vierecks  Dazu wird das Viereck in ein Trapez und Dreieck unterteilt.
Dazu wird das Viereck in ein Trapez und Dreieck unterteilt.
 Über die jeweilige Flächeninhaltsformel können dann die Inhalte der Teilflächen berechnet werden:
Über die jeweilige Flächeninhaltsformel können dann die Inhalte der Teilflächen berechnet werden:

1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(58,7^\circ)&=&\dfrac{e}{7\,\text{cm}}\quad \scriptsize \mid\;\cdot 7\,\text{cm} \\[5pt]
\sin(58,7^\circ)\cdot 7\,\text{cm}&=&e\\[5pt]
e&=&6\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/0aa210e3ee68016e461a67cd80468302a45c9c6bbf44784f2bda2ca564bc75bc_light.svg)
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{EB}^2+e^2&=&(7\,\text{cm})^2\quad \scriptsize \mid\;-e^2 \\[5pt]
\overline{EB}^2&=&(7\,\text{cm})^2-e^2\quad \scriptsize \mid\;\sqrt{\,\,\,}\\[5pt]
\overline{EB}&=&\sqrt{(7\,\text{cm})^2-e^2}\\[5pt]
&=&\sqrt{(7\,\text{cm})^2-(6\,\text{cm})^2}\\[5pt]
\overline{EB}&=&3,6\,\text{cm}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/59bb6fef1b56e743e6788060895144ddc35d24a9f61cf6e0e353b22bc4ecddc2_light.svg)
3. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}&=&\overline{AB}-\overline{EB}\\[5pt]
&=&8,9\,\text{cm}-3,6\,\text{cm}\\[5pt]
\overline{AE}&=&5,3\,\text{cm}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5c1883577336abfa3ef989bdad1ded64fb0d54fc6d38fd709a46b574c3a023c2_light.svg)
4. Schritt: Flächeninhalte der Teilfächen berechnen
![\(\begin{array}[t]{rll}
A_{EBC}&=&\frac{1}{2}\cdot \overline{EB}\cdot e \\[5pt]
&=&\frac{1}{2}\cdot 3,6\,\text{cm}\cdot 6\,\text{cm} \\[5pt]
A_{EBC}&=&10,8\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/beb1cf4f34c1c78a11187c7b4234b0112837fafbfc67d0eba653b9e999bc76a0_light.svg)
![\(\begin{array}[t]{rll}
A_{AECD}&=&\frac{1}{2}\cdot \left(\overline{AD}+ e\right)\cdot \overline{AE} \\[5pt]
&=&\frac{1}{2}\cdot \left(4\,\text{cm}+6\,\text{cm}\right)\cdot 5,3\,\text{cm} \\[5pt]
A_{AECD}&=& 26,5\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1a53045be2490d56478e551fe8379681b8d0057bb9a3afa40034fff89543801f_light.svg)
5. Schritt: Flächeninhalt von
1
Unterteile das Viereck in geeignete Teilfiguren und berechne damit den Flächeninhalt des Vierecks.
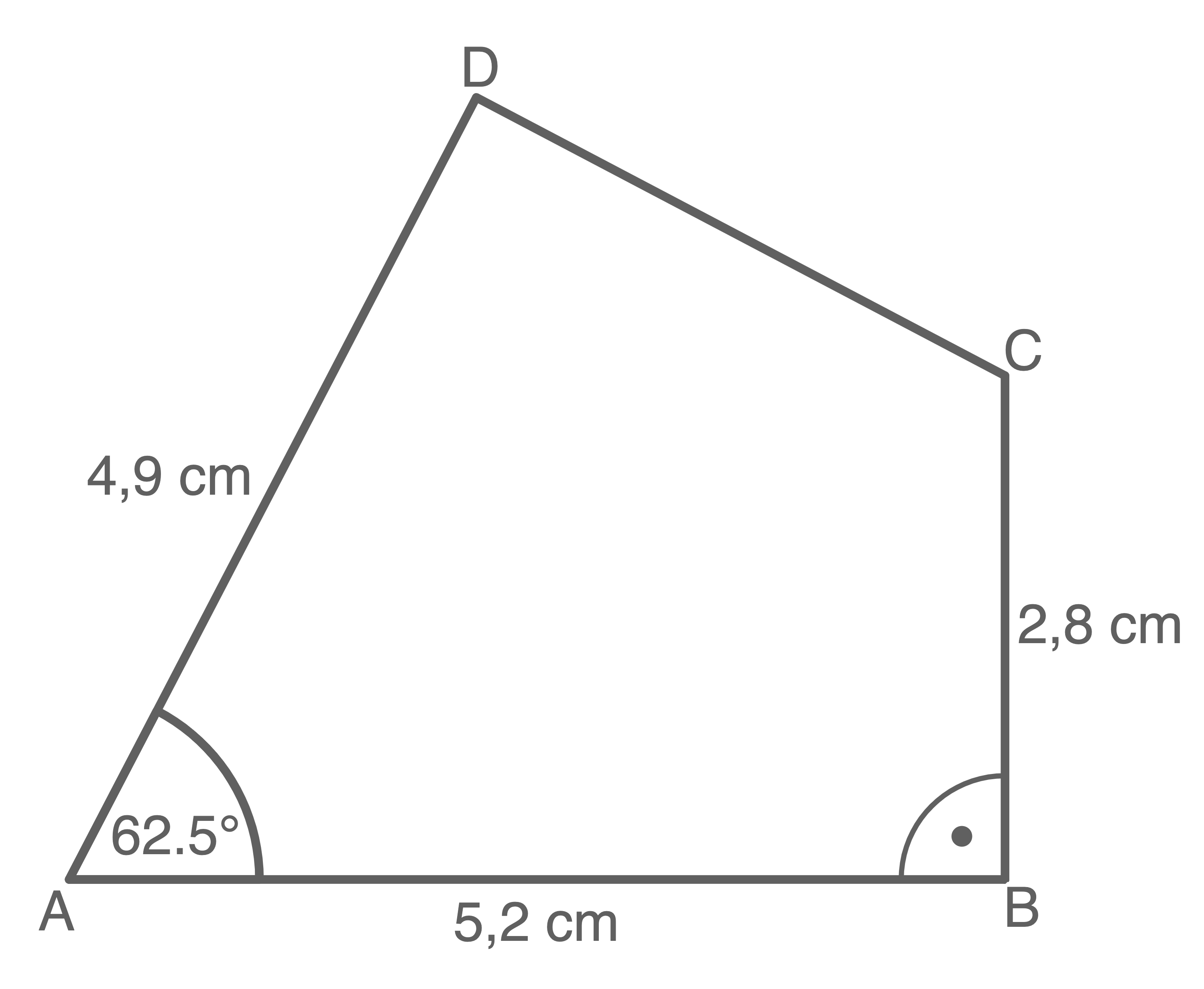
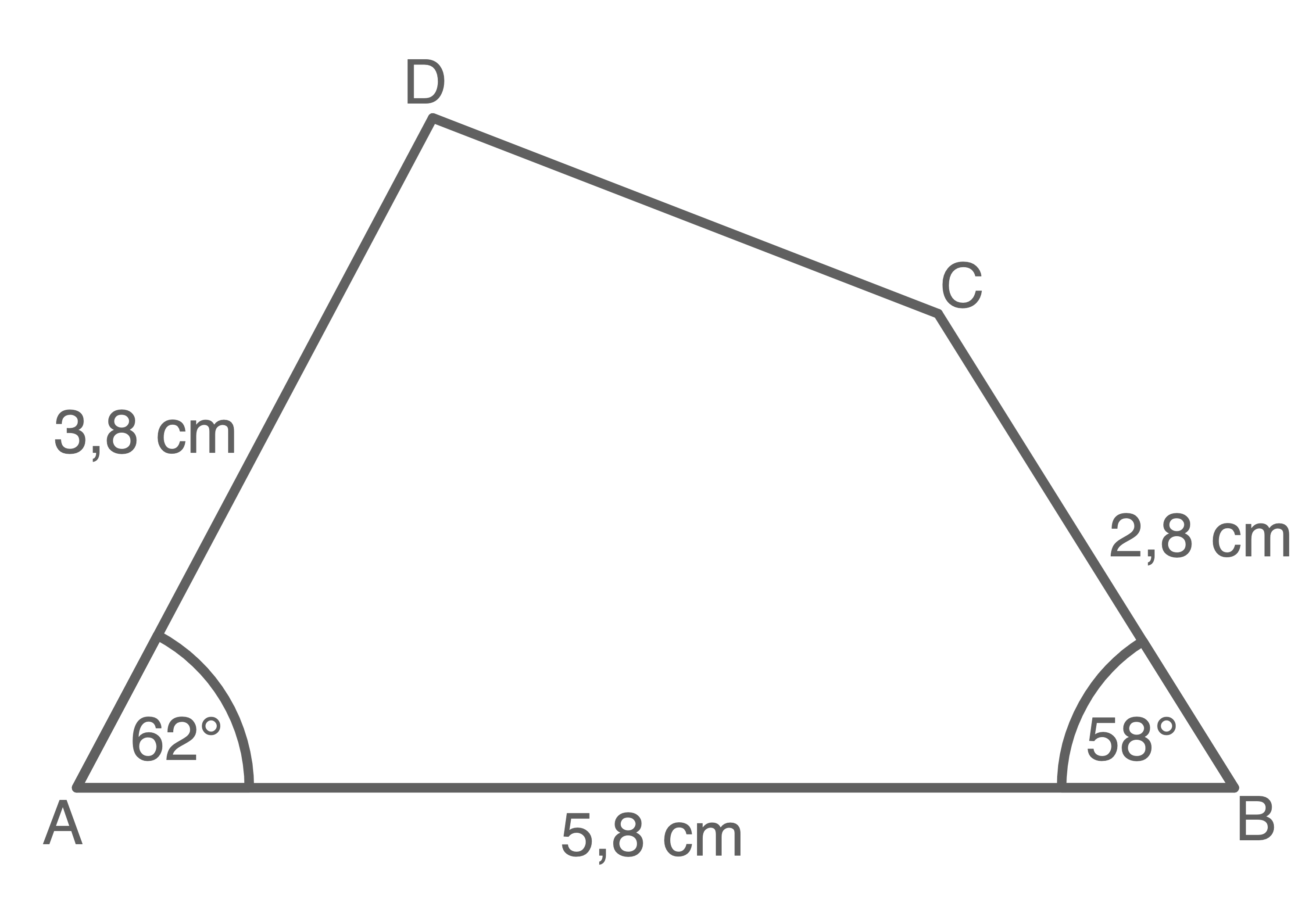
a)

b)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
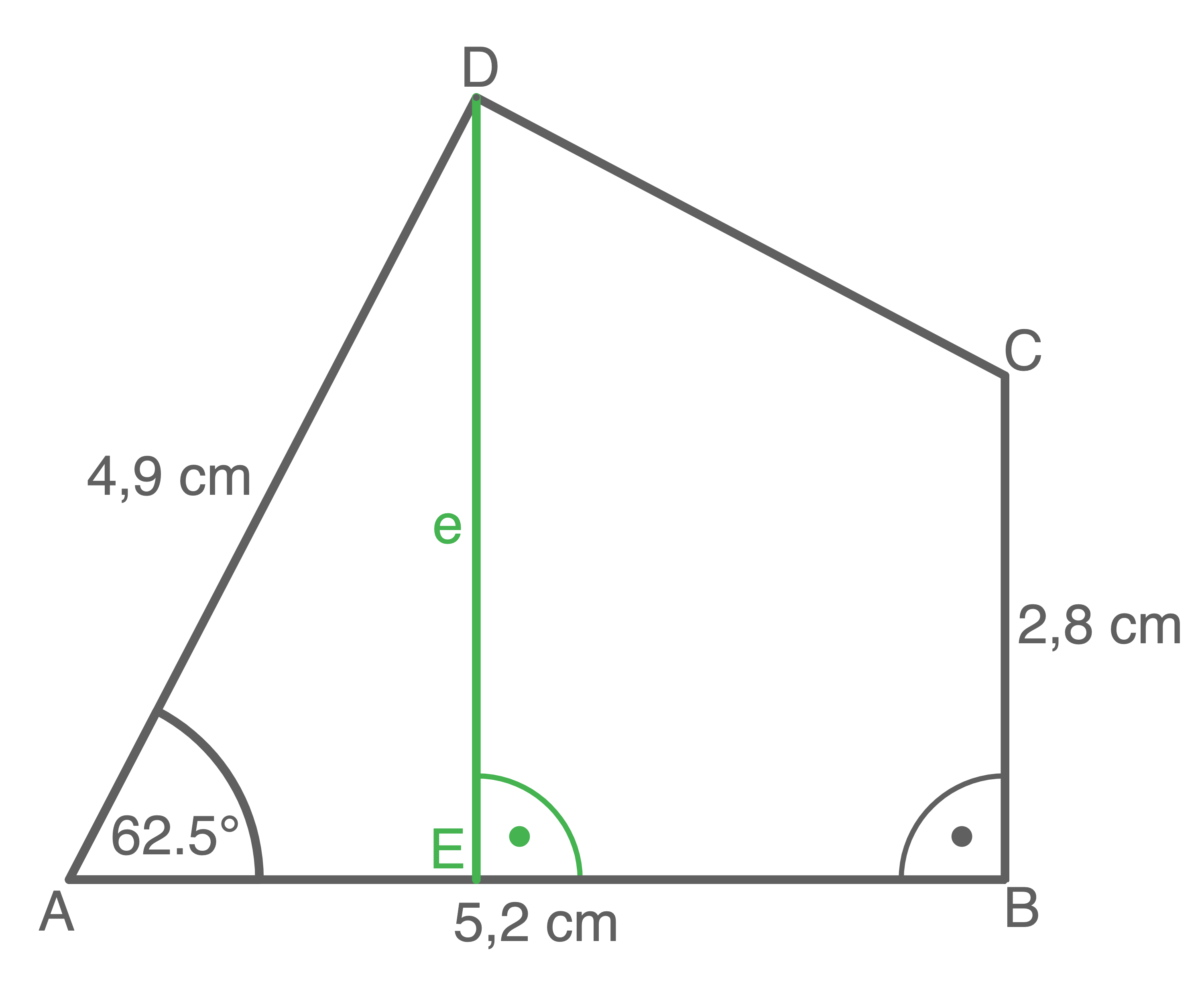
b)