Lineare Funktionen
Als lineare Funktion bezeichnet man eine Funktion mit der Gleichung  Der Graph einer linearen Funktion nennt sich Gerade. Dabei ist
Der Graph einer linearen Funktion nennt sich Gerade. Dabei ist  die Steigung.
die Steigung.
 beschreibt den
beschreibt den  -Achsenabschnitt, also den Abschnitt, an dem der Graph die
-Achsenabschnitt, also den Abschnitt, an dem der Graph die  -Achse im Punkt
-Achse im Punkt  schneidet.
Formeln zur Berechnung der Steigung
schneidet.
Formeln zur Berechnung der Steigung  Liegen die beiden Punkte
Liegen die beiden Punkte  und
und  auf der Geraden, so kann die Steigung mit folgender Formel berechnet werden:
auf der Geraden, so kann die Steigung mit folgender Formel berechnet werden:
 Für parallele Geraden gilt:
Für parallele Geraden gilt:  Für zueinander senkrechte Geraden gilt:
Für zueinander senkrechte Geraden gilt:  bzw.
bzw. 
1
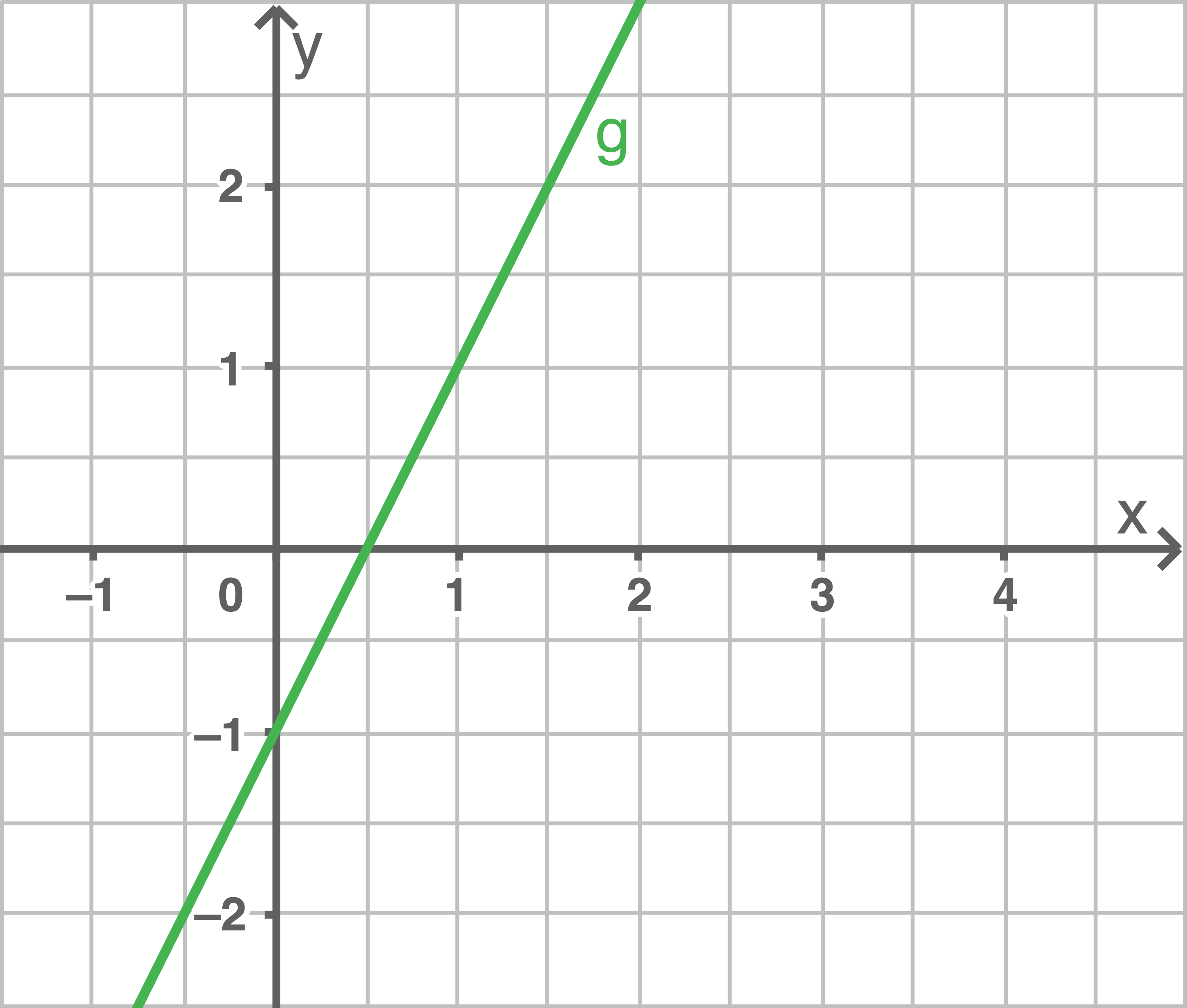
Gib die Gleichung der linearen Funktion an, indem du  abliest und
abliest und  über ein Steigungsdreieck bestimmst.
über ein Steigungsdreieck bestimmst.
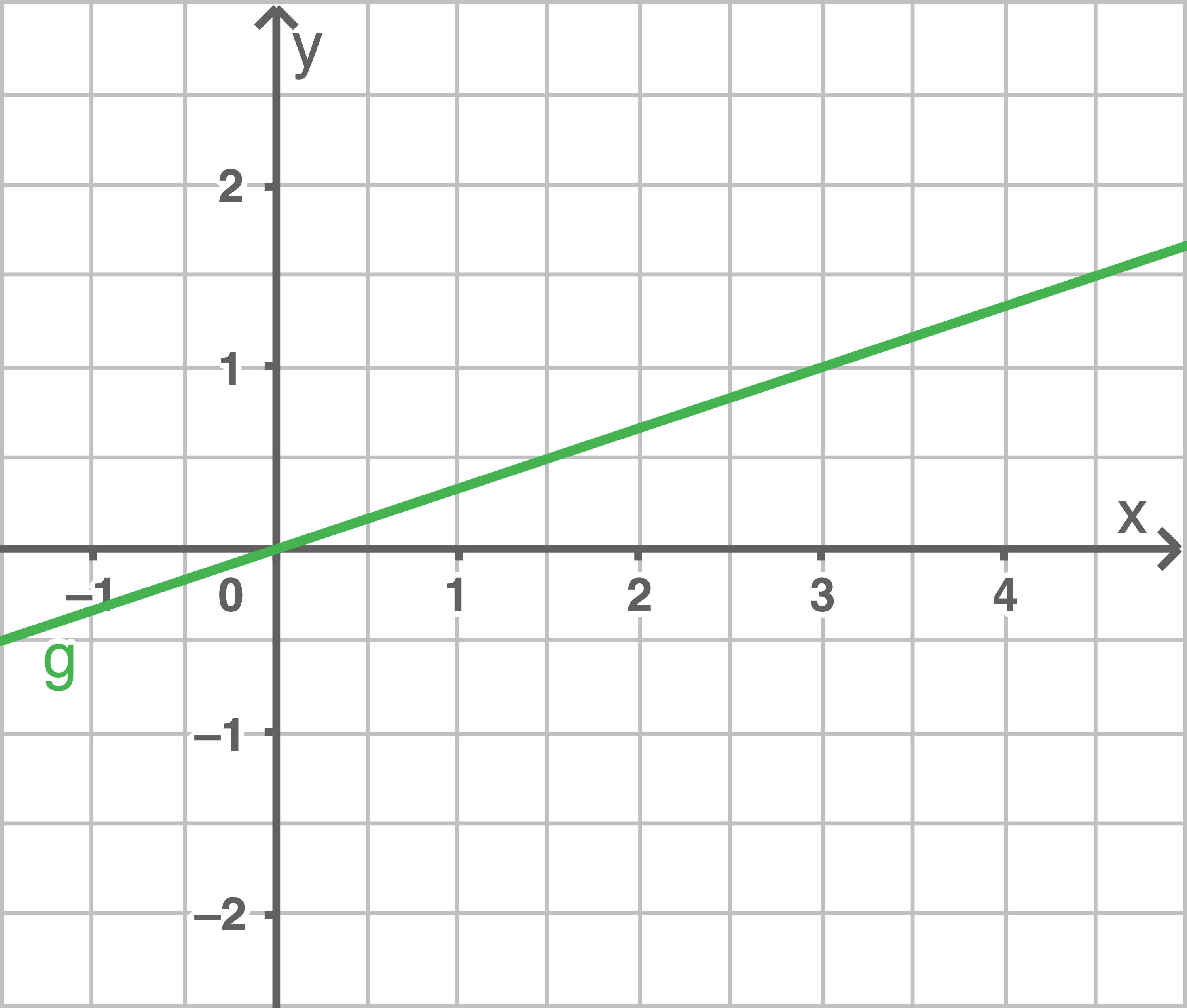
a)

b)

2
Gegeben sind zwei Punkte  und
und  auf einer Geraden
auf einer Geraden  Gib die Gleichung der Geraden an.
Gib die Gleichung der Geraden an.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
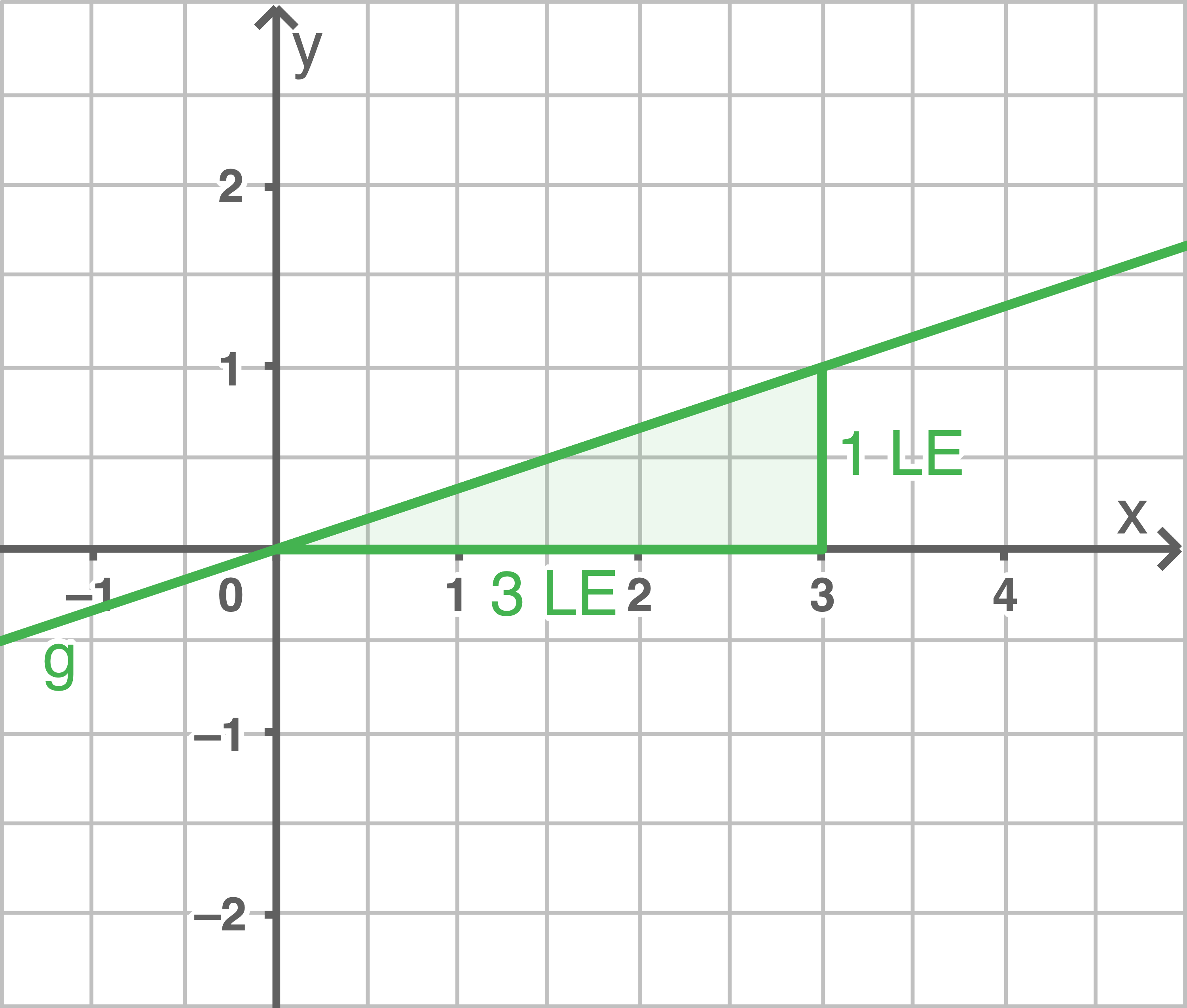
b)
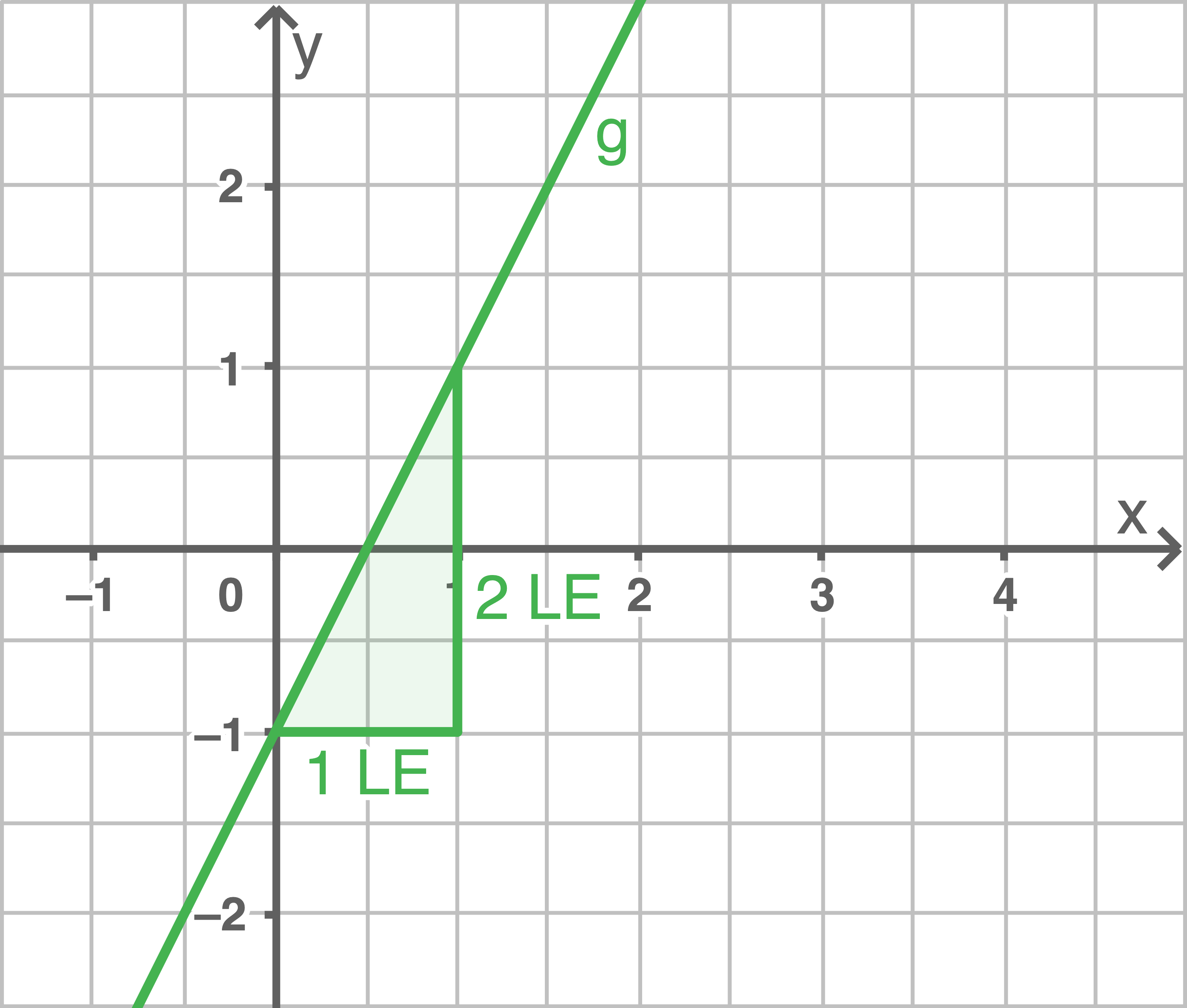
2
a)
b)
c)
d)