Grenzwerte und Asymptoten

Potenzfunktionen mit negativem ganzzahligem Exponent sind für $x=0$ nicht definiert, sie haben dort eine Definitionslücke. Für große $x$ -Werte, sowohl positiv als auch negativ, nähert sich der Graph von Potenzfunktionen mit negativen ganzzahligen Exponenten der $x$ -Achse an, berührt sie jedoch nie. Für $x$ -Werte, die sehr nah an Null liegen, nähert sich der Graph der $y$ -Achse an.

Geraden, denen sich Graphen in dieser Weise immer weiter nähern, ohne sie zu berühren, heißen Asymptoten. Definitionslücken ergeben häufig senkrechte Asymptoten.

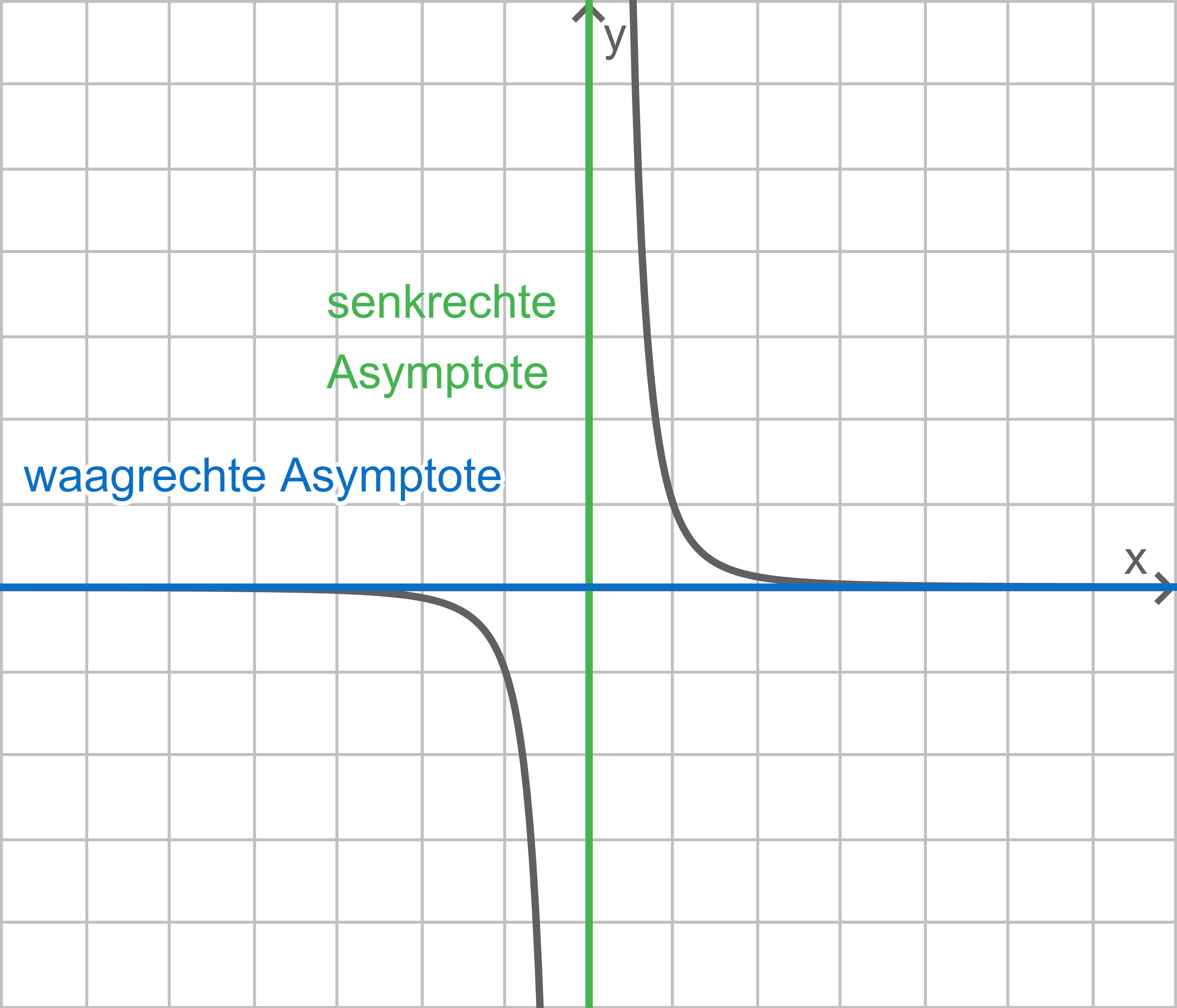
Graph einer Funktion mit senkrechter und waagerechter Asymptote, beschriftet in grün und blau.

$f(x)=x^{-3}$

Zahlen, denen die Funktionswerte einer Funktion $f$ für extrem groß werdende negative bzw. positive $x$ -Werte sehr nah kommen, ohne sie jemals zu erreichen, nennt man Grenzwerte von $f$ für x gegen minus bzw. plus unendlich. Man sagt auch, $\boldsymbol{f}$ geht gegen den Grenzwert. Grenzwerte können auch auftreten, wenn sich Funktionen $x$ -Werten nähern, für welche sie nicht definiert sind.

Beispiel

Der Graph in der Abbildung gehört zu der Potenzfunktion $f(x)=3x^{-2}.$ Ihre Funktionswerte nähern sich für große Werte von $x$ immer weiter der $y$ -Achse an, und für Werte sehr nah an Null geht die Funktion gegen plus unendlich. Damit besitzt $f$ die waagerechte Asymptote $y=0,$ sowie die senkrechte Asymptote $x=0$ und $y=0$ ist der Grenzwert von $f$ gegen plus unendlich. Zudem ist plus unendlich der Grenzwert von $f$ gegen Null. Die beiden Grenzwerte werden wie folgt notiert:

$\lim\limits_{x\to+\infty}f(x)=0$

$\lim\limits_{x\to0}f(x)=+\infty$

Graph einer mathematischen Funktion mit grüner Kurve in einem Koordinatensystem.

Die Gleichungen $x=0$ und $y=0$ beschreiben die beiden Koordinatenachsen. Eine mögliche Lösung ist damit die Funktion aus dem Beispiel in der Einführung, $f(x)=3x^{-2}.$

Die Parameter $d$ bzw. $e$ aus der allgemeinen Funktionsgleichung einer Potenzfunktion verschieben den Graphen der Potenzfunktion in $x$ - bzw. $y$ -Richtung. Dabei verschieben sich auch die Asymptoten der Funktion. Die Funktion $f(x)=3x^{-2}$ besitzt die beiden Koordinatenachsen als Asymptoten. Mit den Parametern $d=3$ und $e=0$ lassen sich somit die beiden, zu den Gleichungen aus der Aufgabenstellung gehörenden, Asymptoten zu erhalten. Damit ergibt sich $g(x)=3\cdot{(x-3)}^{-2}$ als mögliche Funktion, die die beiden gewünschten Asymptoten besitzt.

Mit der gleichen Methode wie in Aufgabenteil b) lässt sich auch hier aus $f$ eine Funktion konstruieren, die die beiden angegebenen Asymptoten besitzt. Dieses Mal muss $f$ um $\frac{1}{5}$ in $y$ -Richtung verschoben werden. Mit den Parametern $d=0$ und $e=\frac{1}{5}$ ergibt sich somit eine Gleichung für eine mögliche Funktion:

$h(x)=3x^{-2}+\dfrac{1}{5}$

Auch in diesem Fall ergibt sich wieder eine mögliche Funktion durch Verschieben von $f$ . Dieses Mal muss $f$ um $10$ Längeneinheiten in $x$ -Richtung und um zwei Längeneinheiten gegen $y$ -Richtung verschoben werden. Somit ergeben sich die Parameter $d=10$ und $e=-2$ und damit eine mögliche Lösung durch die Funktion mit der Gleichung $i(x)=3\cdot{(x-10)}^{-2}-2.$

Die graphische Darstellung des CAS liefert:

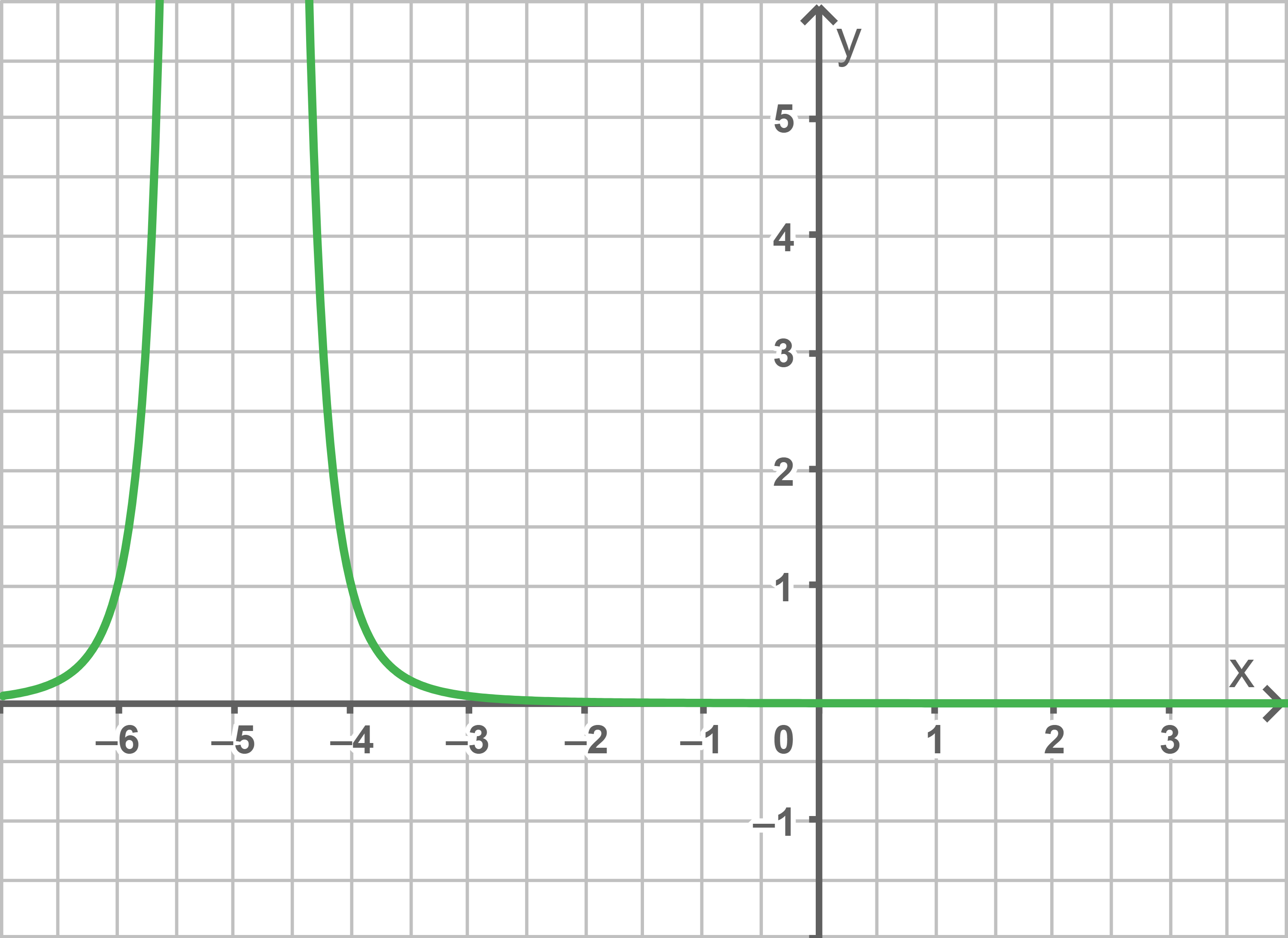Graph einer mathematischen Funktion auf einem Koordinatensystem mit Achsen und Gittern.

Mit Hilfe des Graphs folgt also, dass $\lim\limits_{x\to+\infty}f(x)=0$ gilt.

Für den Graph von $g$ ergibt sich:

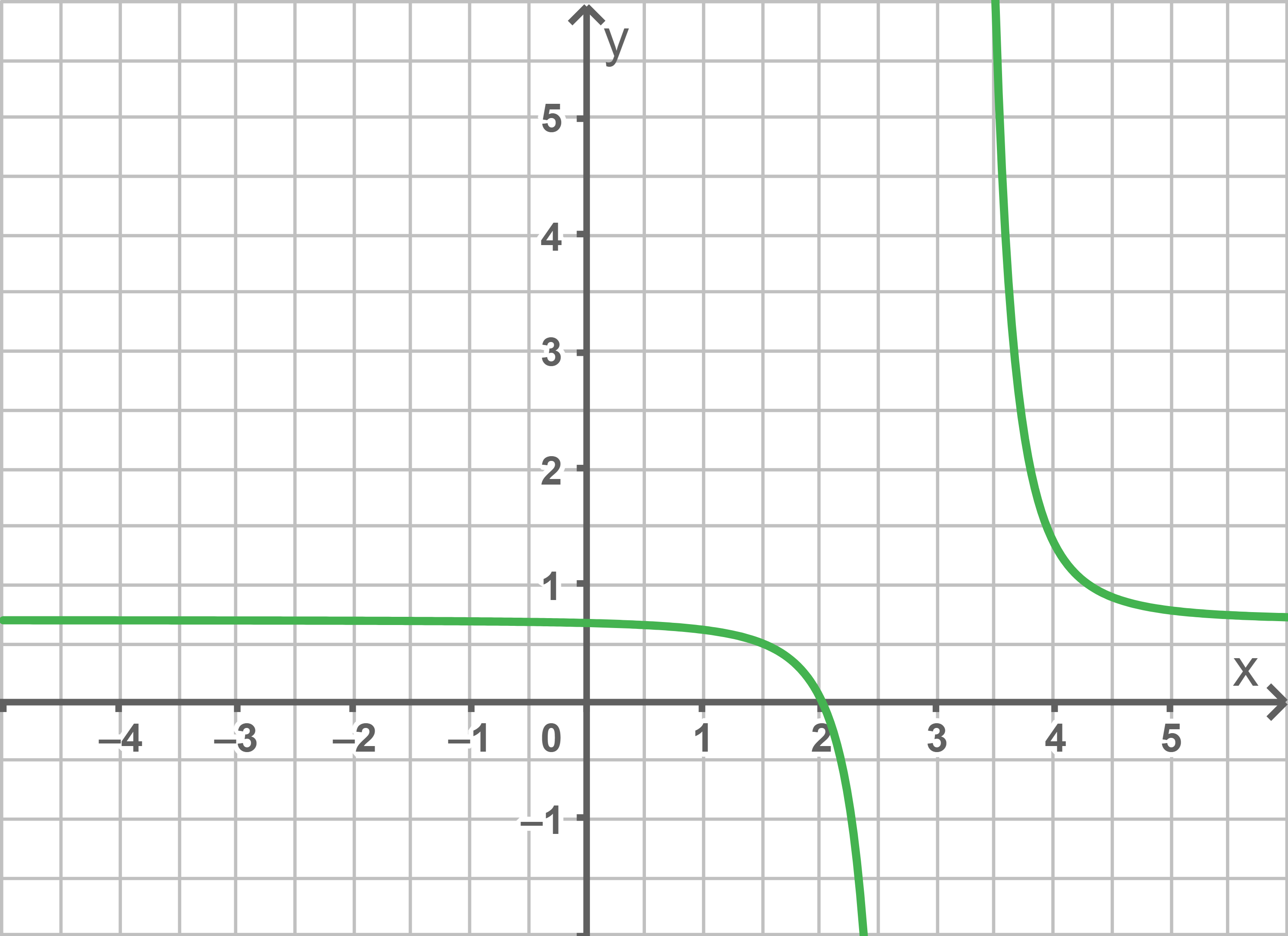Graf einer mathematischen Funktion im Koordinatensystem mit gitterartigen Linien.

Für den gesuchten Grenzwert ergibt sich somit $\lim\limits_{x\to-\infty}g(x)=\frac{7}{10}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?