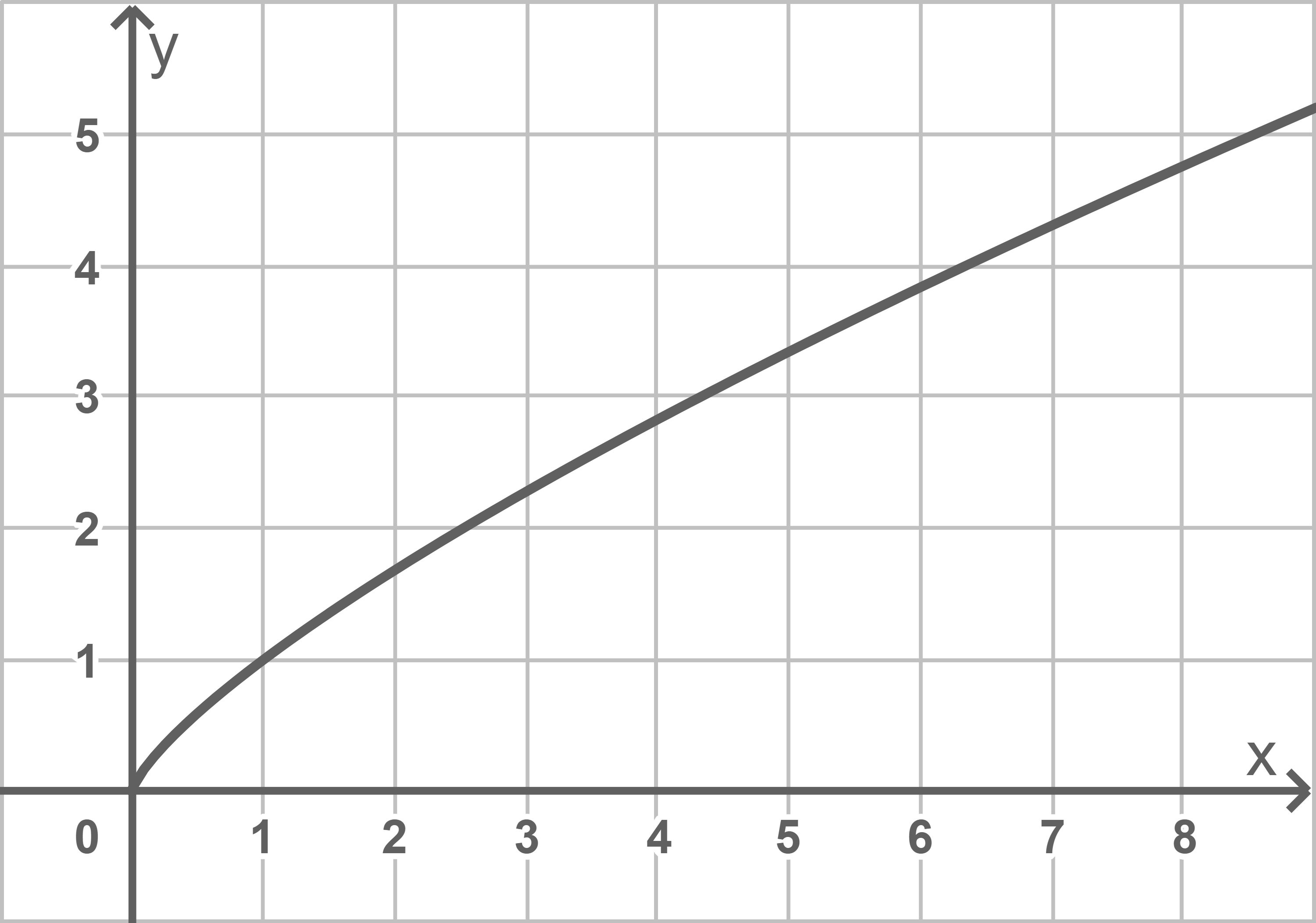
Wurzelfunktionen
Mit Hilfe der Wurzelschreibweise von Potenzen mit rationalen Exponenten können Potenzfunktionen, die rationale Exponenten 
besitzen, in der Form ![\(f(x)=\sqrt[n]{x^m}\)](https://mathjax.schullv.de/2e0c934a9a5f543261585b60ca95b4e2919ac4112f573bd174507470a1e94fbb?color=5a5a5a)
geschrieben werden. Diese Wurzelform gibt den Potenzfunktionen mit rationalen Exponenten 
ihre Namen: Wurzelfunktionen. Für 
sind die Wurzelfunktionen die Umkehrfunktionen von Potenzfunktionen mit natürlichen Exponenten:
Definition
Jede Potenzfunktion der FormEigenschaften
- Der Definitionsbereich und der Wertebereich einer Wurzelfunktion sind die nicht-negativen reellen Zahlen
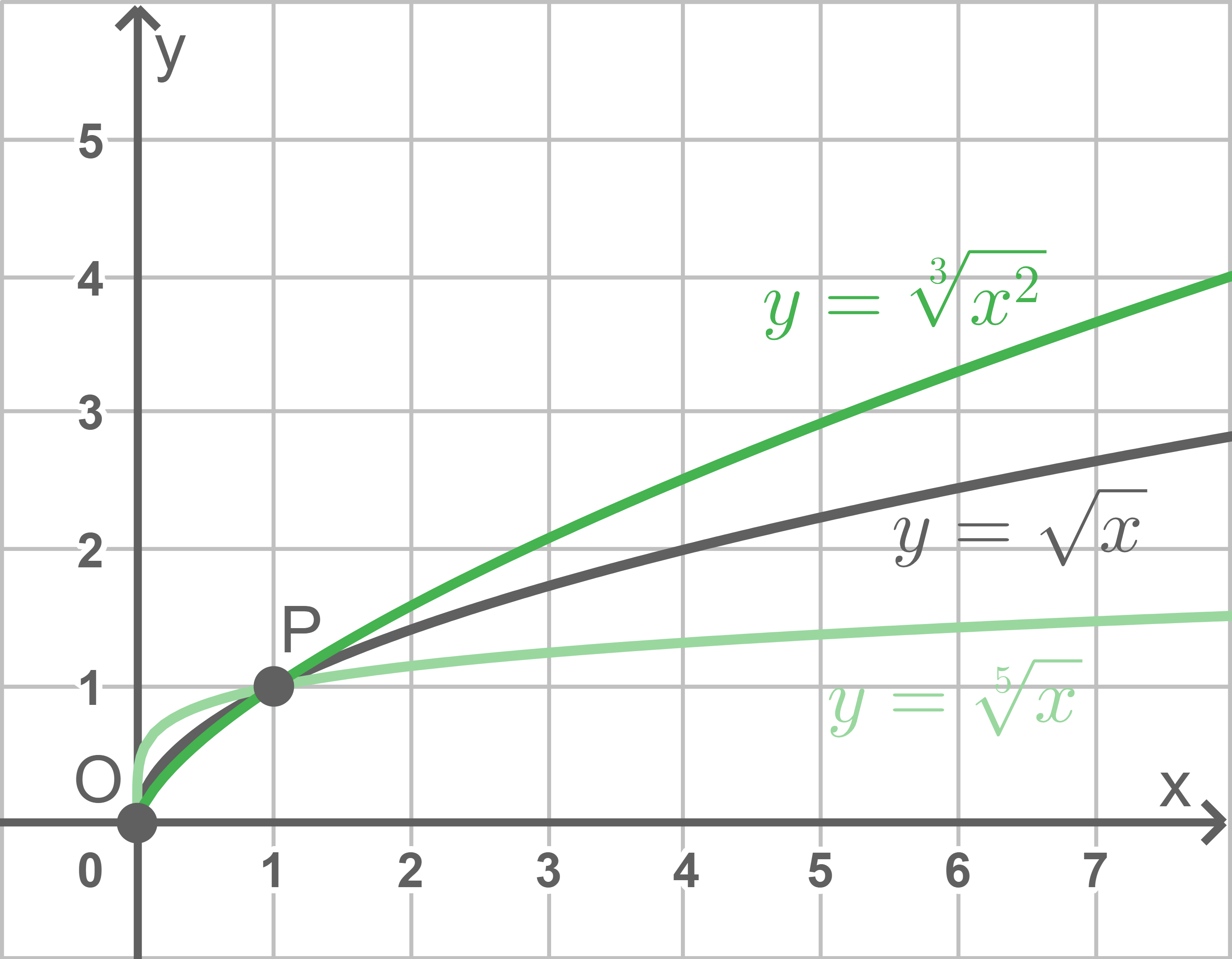
- Der Graph jeder Wurzelfunktion verläuft durch die Punkte
und
- Wurzelfunktionen verlaufen im gesamten Definitionsbereich monoton steigend
1
Rechne mit Hilfe des CAS nach, ob ein passender Wert 
existiert, sodass der jeweilige Punkt auf dem Graphen einer Wurzelfunktion der Form ![\(f(x)=\sqrt[k]{x}\)](https://mathjax.schullv.de/8e912721878c5f9dff872d1f124cb424abe71bec5ec4c126254c9d64886be143?color=5a5a5a)
liegt. Falls dies der Fall ist, gib einen der für bestimmten Werte an.
a)
b)
c)
d)
2
Zeichne den Graph der zu der jeweiligen Funktionsgleichung passenden Wurzelfunktion in ein Koordinatensystem ein.
![\(f(x)=\sqrt[3]{x}\)](https://mathjax.schullv.de/66969a667e5fff593e8420143978eb87156d8c28d2e9a8f24f0bb0f5887e8ca8?color=5a5a5a)
![\(g(x)=\sqrt[4]{x^3}\)](https://mathjax.schullv.de/b528116fc6a69687b7b43ba767d83b494476ecf6e1d48e97f5c73a6aca9b6dc4?color=5a5a5a)
a)
b)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Durch Einsetzen der Koordinaten des Punkts 
in die gegebene Gleichung folgt:
![\(\begin{array}[t]{rll}
2&=&\sqrt[k]{4} \\[5pt]
&=&4^{\frac{1}{k}}
\end{array}\)](https://mathjax.schullv.de/f384bcf0a33480ffe12ea5561152ac1e82aee621966dce9799d4ab876feb35a5?color=5a5a5a)
Damit der Punkt auf dem Graph einer Wurzelfunktion der gegebenen Form liegt, muss für diese Gleichung eine natürliche Zahl, welche größer als 
ist, als Lösung für existieren. Mit dem solve-Befehl des CAS folgt:
b)
Der Punkt mit den Koordinaten 
liegt, genau wie der Punkt mit den Koordinaten 
auf den Graphen aller Wurzelfunktionen. Somit ist hier jede natürliche Zahl größer als eine Lösung für 
zum Beispiel 
c)
Der Wertebereich aller Wurzelfunktionen ist die Menge der nicht-negativen reellen Zahlen. Da der Punkt 
die 
-Koordinate 
besitzt, kann er nicht auf dem Graphen einer Wurzelfunktion liegen. Somit existiert kein Wert für 
d)
Einsetzen der Koordinaten von 
in die Gleichung aus der Aufgabenstellung liefert:
![\(\begin{array}[t]{rll}
\dfrac{5}{6}&=&\sqrt[k]{\dfrac{125}{216}} \\[5pt]
&=&\left(\dfrac{125}{216}\right)^{\frac{1}{k}}
\end{array}\)](https://mathjax.schullv.de/07167515d3bf6df2f83c33af3de0b4fc6200db7fb88ed9c9c19d44b4d529301d?color=5a5a5a)
Mit dem solve-Befehl des CAS ergibt sich:
Für liegt der Punkt 
somit auf dem Graphen einer Wurzelfunktion der Form ![\(f(x)=\sqrt[k]{x}.\)](https://mathjax.schullv.de/732a6e1d0cffb2557a8b18307f9426f5d9af50597e57578a5cc5dd15e2e94a45?color=5a5a5a)
2
a)
Mit Hilfe einer Wertetabelle im Taschenrechner folgt für den Graphen der Wurzelfunktion der Form ![\(f(x)=\sqrt[3]{x}:\)](https://mathjax.schullv.de/b2d0db09cb90d17886de0def7129f1c4ddb98976d5b91574b0ab6003e0637334?color=5a5a5a)
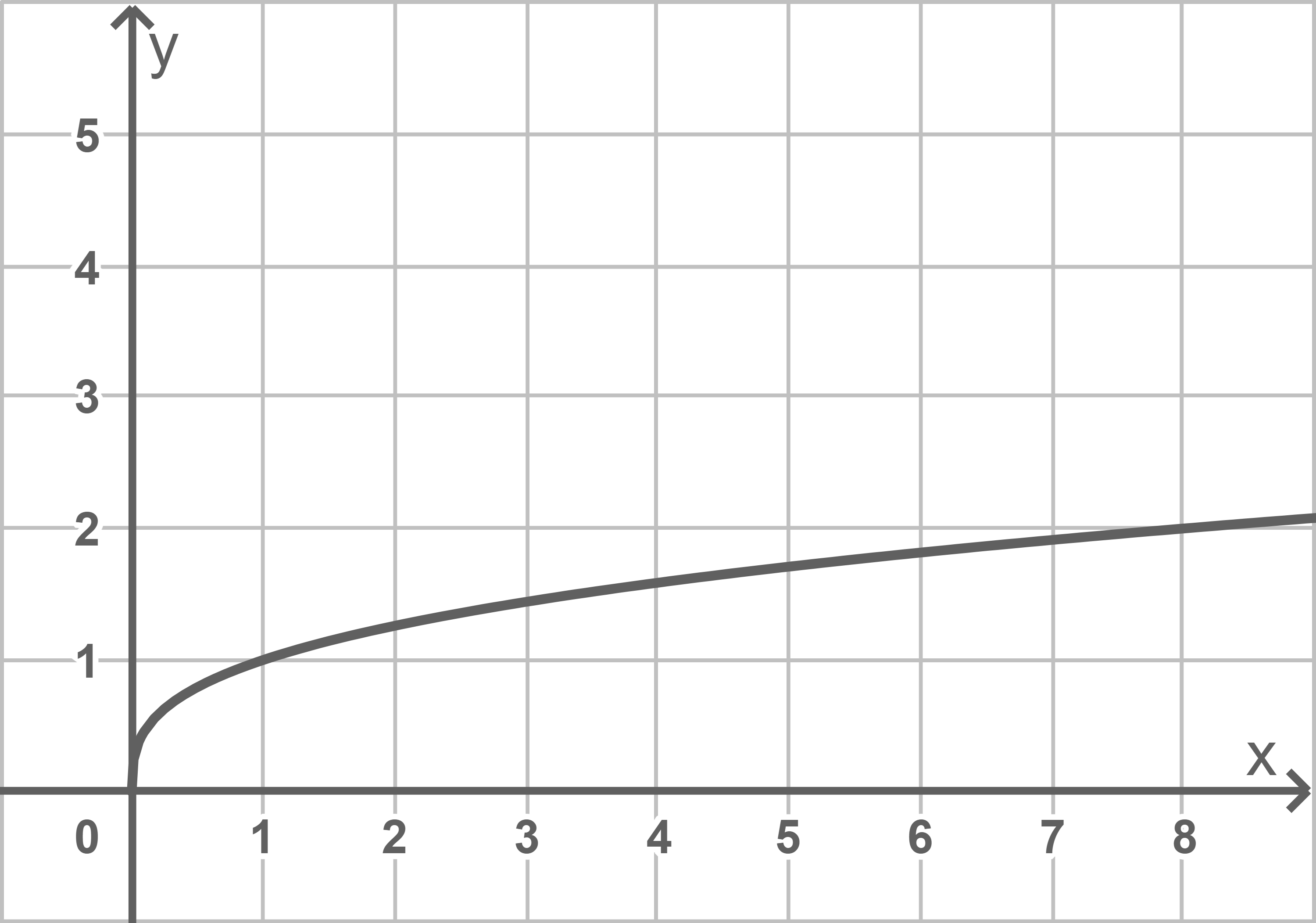
b)
Eine im Taschenrechner erstellte Wertetabelle liefert folgenden Graph für die Wurzelfunktion mit der Funktionsgleichung ![\(f(x)=\sqrt[4]{x^3}:\)](https://mathjax.schullv.de/a4c9d8f3b06b6b30076e7b975023e1b0715f41d10c0f3804c22e85ff20dad7b2?color=5a5a5a)
