Potenzfunktionen mit negativen ganzzahligen Exponenten

Potenzfunktionen können nicht nur positive Exponenten besitzen, sondern auch negative:

Der Graph einer Potenzfunktion $f(x)=a\cdot x^{-n}$ mit $a\neq0$ und $n$ einer natürlichen Zahlen größer Null wird Hyperbel n-ter Ordnung genannt.

Eigenschaften

Der Graph einer Potenzfunktion $f(x)=x^{-n}$ mit einer natürlichen Zahl $n$ größer Null hat die folgenden Eigenschaften:

Der Graph verläuft durch den Punkt $(1\mid 1).$

Für gerade $n$ ist der Graph achsensymmetrisch zur $y$ -Achse.

Für ungerade $n$ ist der Graph punktsymmetrisch zum Ursprung.

Für gerade $n$ nimmt die Funktion nur die positiven reellen Zahlen an.

Für ungerade $n$ nimmt die Funktion alle reellen Zahlen außer die Null an.

Beispiele

Gerades $\boldsymbol{n}$

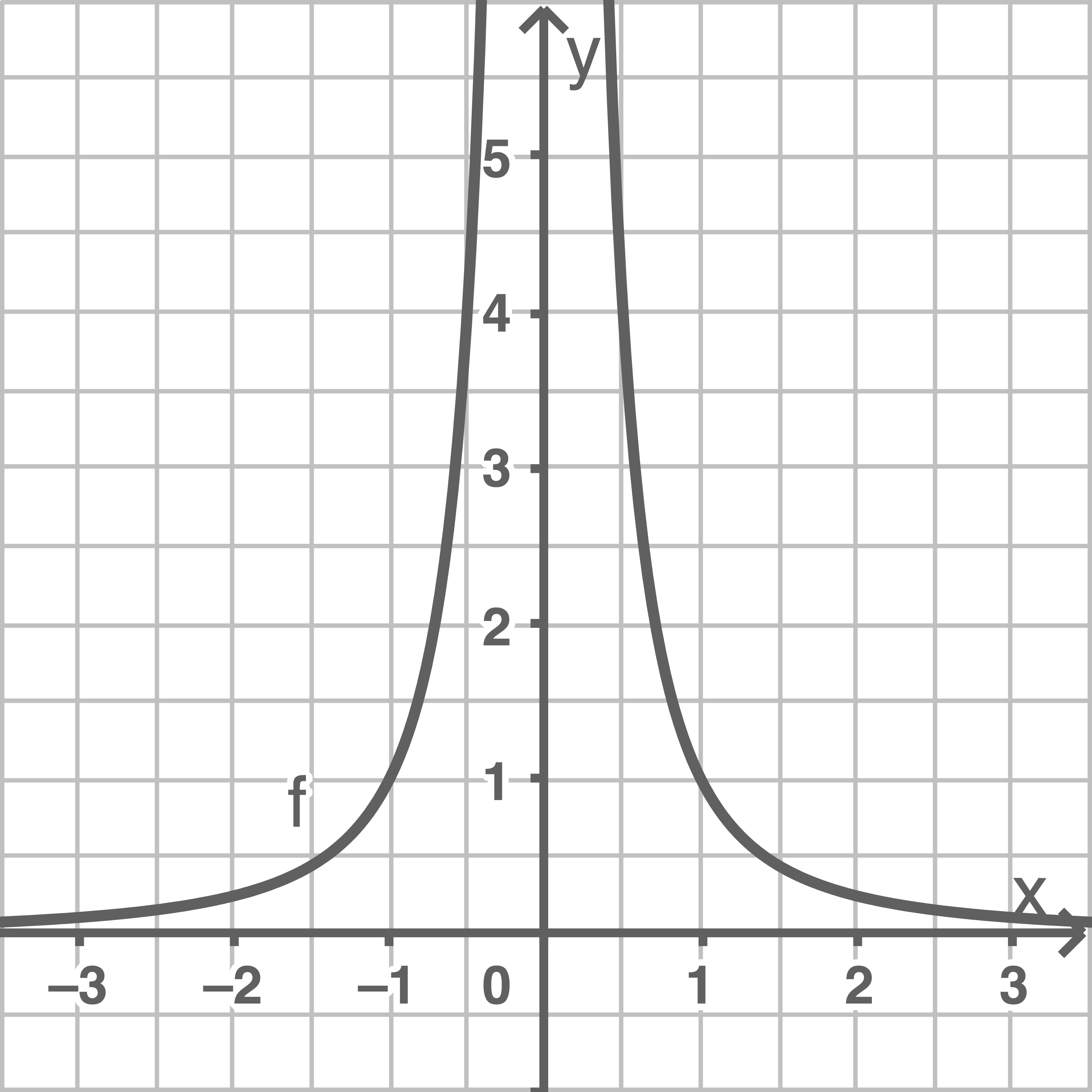
potenzfunktion mit ganzzahligem negativem exponenten

$f(x)=x^{-2}$

Ungerades $\boldsymbol{n}$

$g(x)=x^{-3}$

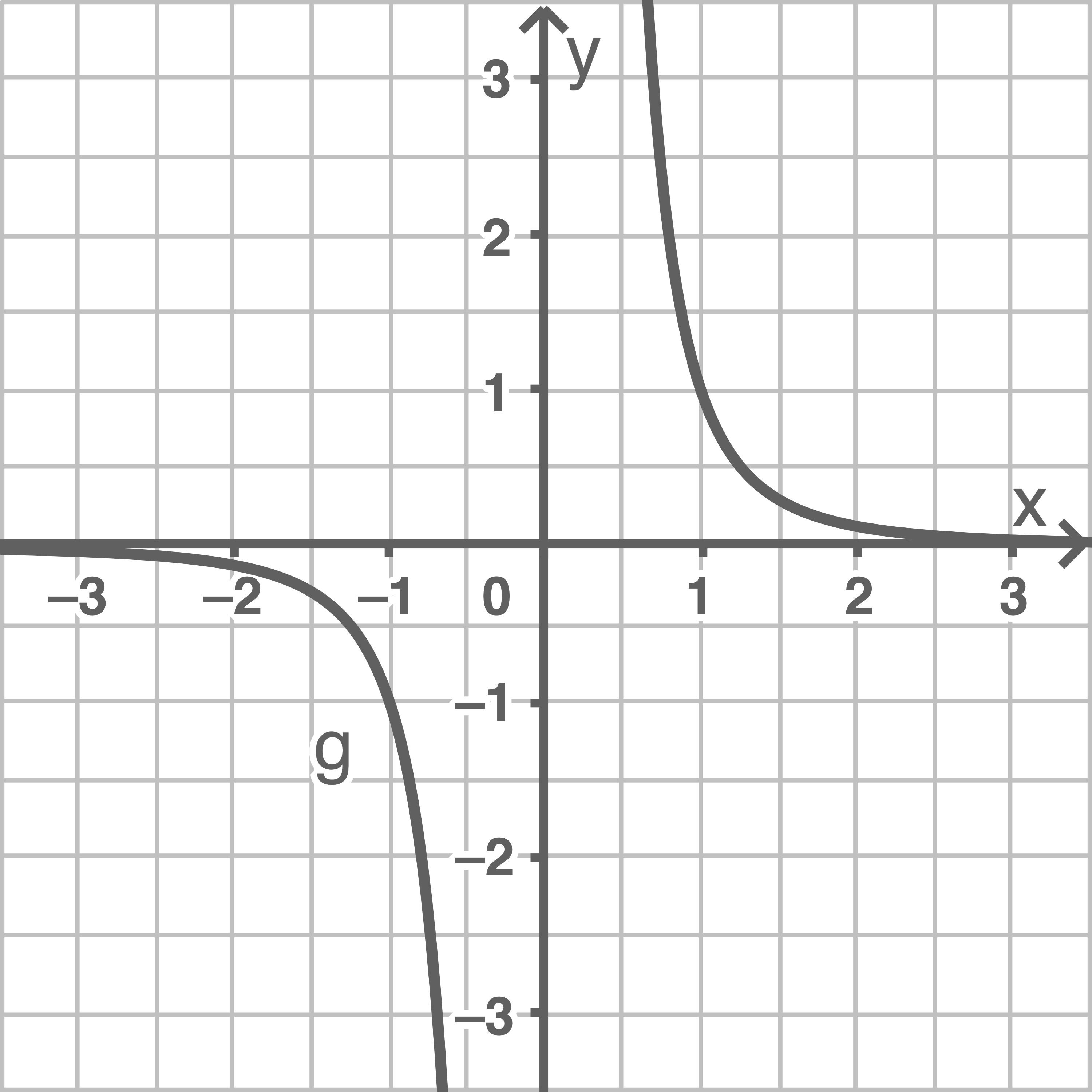
Die Parameter $a,d$ und $e$ in der Funktionsgleichung $f(x)=a\cdot(x-d)^{-n}+e$ haben die gleichen Auswirkungen auf den Graphen einer Potenzfunktion mit ganzzahligem negativem Exponent, wie die bereits kennengelernten Auswirkungen auf die Graphen der Potenzfunktionen mit natürlichen Exponenten.

Fülle die Tabellen mithilfe der Symmetrieeigenschaften aus.

$\color{#ffffff}{x}$	$5$	$2$	$0,4$	$-0,4$	$-2$	$-5$
$\color{#ffffff}{f(x)=x^{-1}}$	$0,2$	$0,5$	$2,5$

$\color{#ffffff}{x}$	$2$	$0,5$	$0,2$	$-0,2$	$-0,5$	$-2$
$\color{#ffffff}{f(x)=x^{-2}}$	$0,25$	$4$	$25$

$\color{#ffffff}{x}$	$3$	$1,5$	$0,1$	$-0,1$	$-1,5$	$-3$
$\color{#ffffff}{f(x)=x^{-3}}$				$-1\,000$	$-0,3$	$-0,04$

Bestimme den jeweiligen Vorfaktor $a$ der Potenzfunktion mit der Gleichung $f(x)=a\cdot x^{-3}$ mit Hilfe der Koordinaten des auf dem Graphen liegenden Punktes:

$A(2\mid8)$

$B(1\mid20)$

$C(-3\mid2)$

$D\left(\dfrac{1}{2}\;\bigg\vert\;32\right)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Der Exponent der Potenzfunktion ist ungerade, d.h. der Graph ist punktsymmetrisch zum Ursprung. Somit gilt $f(x)=-f(-x)$ und es folgt:

$\color{#ffffff}{x}$	$5$	$2$	$0,4$	$-0,4$	$-2$	$-5$
$\color{#ffffff}{f(x)=x^{-1}}$	$0,2$	$0,5$	$2,5$	$-2,5$	$-0,5$	$-0,2$

Der Exponent der Potenzfunktion ist gerade, d.h. der Graph ist achsensymmetrisch zur $y$ -Achse. Somit gilt $f(x)=f(-x)$ und es folgt:

$\color{#ffffff}{x}$	$2$	$0,5$	$0,2$	$-0,2$	$-0,5$	$-2$
$\color{#ffffff}{f(x)=x^{-2}}$	$0,25$	$4$	$25$	$25$	$4$	$0,25$

Der Exponent der Potenzfunktion ist ungerade, d.h. der Graph ist punktsymmetrisch zum Ursprung. Somit gilt $f(x)=-f(-x)$ und es folgt:

$\color{#ffffff}{x}$	$3$	$1,5$	$0,1$	$-0,1$	$-1,5$	$-3$
$\color{#ffffff}{f(x)=x^{-3}}$	$0,04$	$0,3$	$1\,000$	$-1\,000$	$-0,3$	$-0,04$

$\begin{array}[t]{rlll} f(x)&=&a\cdot x^{-3} \\[5pt] 8&=&a\cdot2^{-3} \\[5pt] 8&=&a\cdot \dfrac{1}{2^3} \\[5pt] 8&=&a\cdot \dfrac{1}{8} &\mid\;\cdot 8\\[5pt] 64&=&a \end{array}$

$\begin{array}[t]{rlll} f(x)&=&a\cdot x^{-3} \\[5pt] 20&=&a\cdot1^{-3} \\[5pt] 20&=&a\cdot \dfrac{1}{1^3} \\[5pt] 20&=&a\cdot\dfrac{1}{1} \\[5pt] 20&=&a \end{array}$

$\begin{array}[t]{rlll} f(x)&=&a\cdot x^{-3} \\[5pt] 2&=&a\cdot(-3)^{-3} \\[5pt] 2&=&a\cdot \dfrac{1}{(-3)^3} \\[5pt] 2&=&a\cdot\dfrac{1}{-27} &\mid\;\cdot (-27)\\[5pt] -54&=&a \end{array}$

$\begin{array}[t]{rlll} f(x)&=&a\cdot x^{-3} \\[5pt] 32&=&a\cdot\left(\dfrac{1}{2}\right)^{-3} \\[5pt] 32&=&a\cdot \dfrac{1}{\frac{1}{2^3}} \\[5pt] 32&=&a\cdot2^3 \\[5pt] 32&=&a\cdot8 &\mid\;:8\\[5pt] 4&=&a \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?