Potenzen mit ganzzahligem Exponent
Wird eine Zahl mehrfach mit sich selbst multipliziert, lässt sich dieses Produkt auch übersichtlich mit der Potenzschreibweise darstellen. Diese Darstellung ist auch für das Produkt von Kehrwerten möglich. Eine Potenz besteht immer aus einer Basis (Grundzahl) und einem Exponenten (Hochzahl).
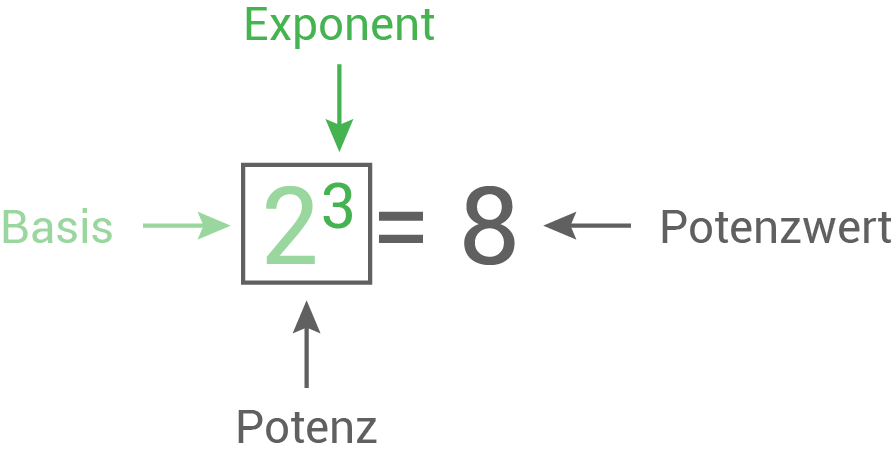Man sagt: „Zwei hoch drei“
Eine besondere Darstellung von einigen Zahlen ist die Schreibweise mit Zehnerpotenzen. Diese wird oft bei sehr großen oder sehr kleinen positiven Zahlen verwendet, um die jeweilige Zahl übersichtlicher darzustellen. Es gilt zum Beispiel 
und 
Für jede reelle Zahl 
gilt:
Zudem wird 
für
definiert.
für
Sonderfälle
für alle natürlichen Zahlen
größer als Null
ist nicht definiert, da nicht durch Null geteilt werden kann
für alle reellen Zahlen
Beispiele
1
Berechne die angegebenen Ausdrücke.
a)
b)
c)
d)
e)
f)
2
Schreibe die folgenden Zahlen in der Schreibweise mit Zehnerpotenzen.
a)
b)
c)
d)
e)
f)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
Nach den Regeln für die Sonderfälle gilt 
d)
e)
f)
2
a)
b)
c)
d)
e)
f)