Sinus- und Kosinussatz

Für den Sinus eines Winkels $\alpha,$ die größer als $90^\circ$ und maximal $180^\circ$ groß sind, gilt die Gleichung $\sin(\alpha)=\sin(180^\circ-\alpha),$ während für den Kosinus $\cos(\alpha)=-\cos(180^\circ-\alpha)$ gilt. Damit lassen sich der Sinussatz und der Kosinussatz herleiten:

Aus jedem Dreieck $ABC$ lässt sich durch einzeichnen einer der drei Höhen des Dreiecks ein rechtwinkliges Dreieck konstruieren. Die Vorgehensweise ist hierbei unterschiedlich, je nachdem ob das Dreieck spitzwinklig oder stumpfwinklig ist:

Spitzwinkliges Dreieck

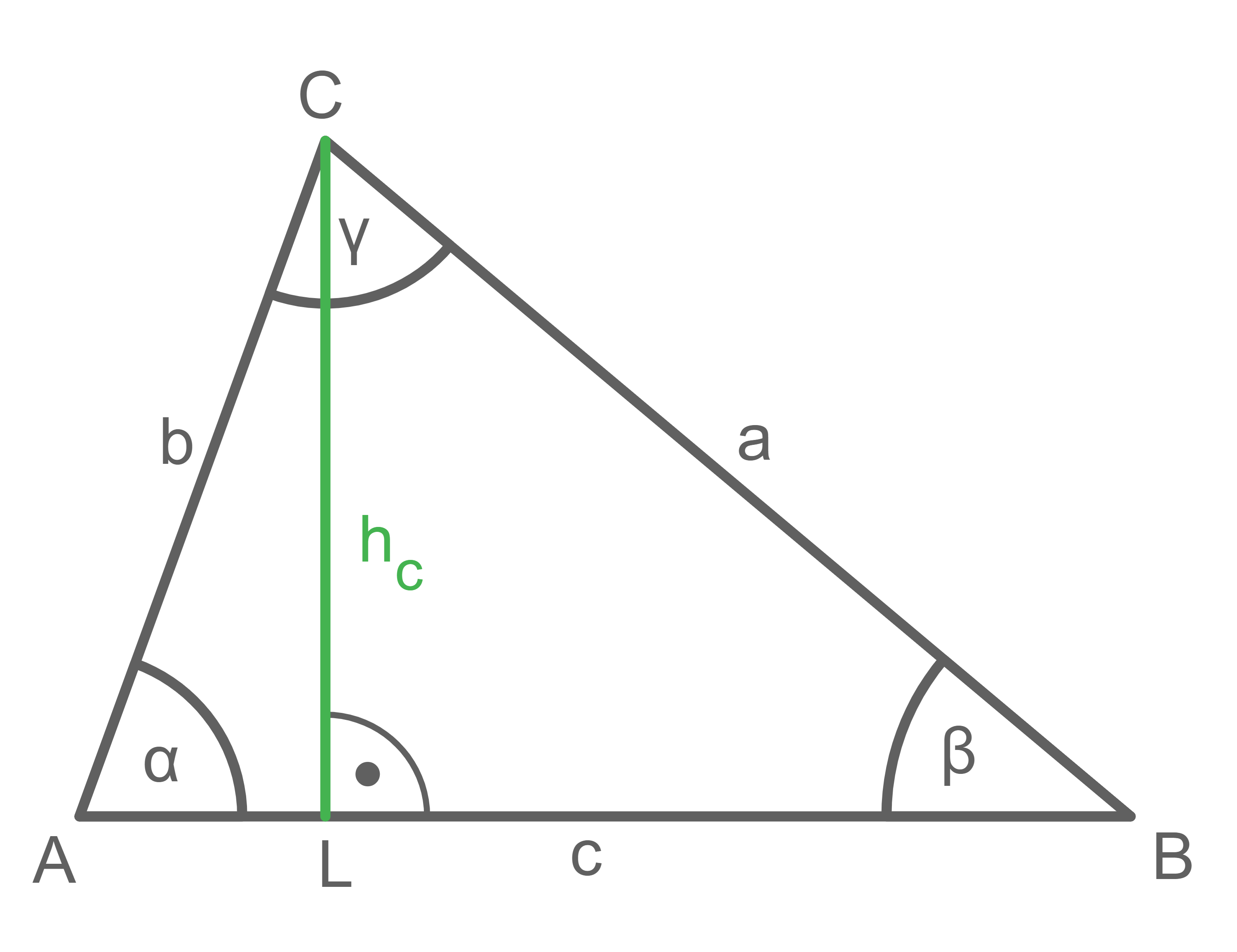Die Grundseite $c$ wird durch die Höhe $h_c$ in zwei Teilstücke geteilt, von denen das kleinere mit $c_1$ und das größere mit $c_2$ bezeichnet wird. Die Höhe $h_c$ teilt das Dreieck $ABC$ in zwei rechtwinklige Dreiecke. In dem linken Teildreieck gilt somit $\sin(\alpha)=\frac{h_c}{b}$ und $\cos(\alpha)=\frac{c_1}{b}.$ Das rechte Teildreieck liefert die Zusammenhänge $\sin(\beta)=\frac{h_c}{a}$ und $a^2={h_c}^2+c^2.$ Diese Gleichungen zusammen ergeben $\boldsymbol{\frac{a}{b}=\frac{\sin(\alpha)}{\sin(\beta)}}$ und $\boldsymbol{a^2=b^2+c^2-2bc\cdot\cos(\alpha)}.$

Stumpfwinkliges Dreieck

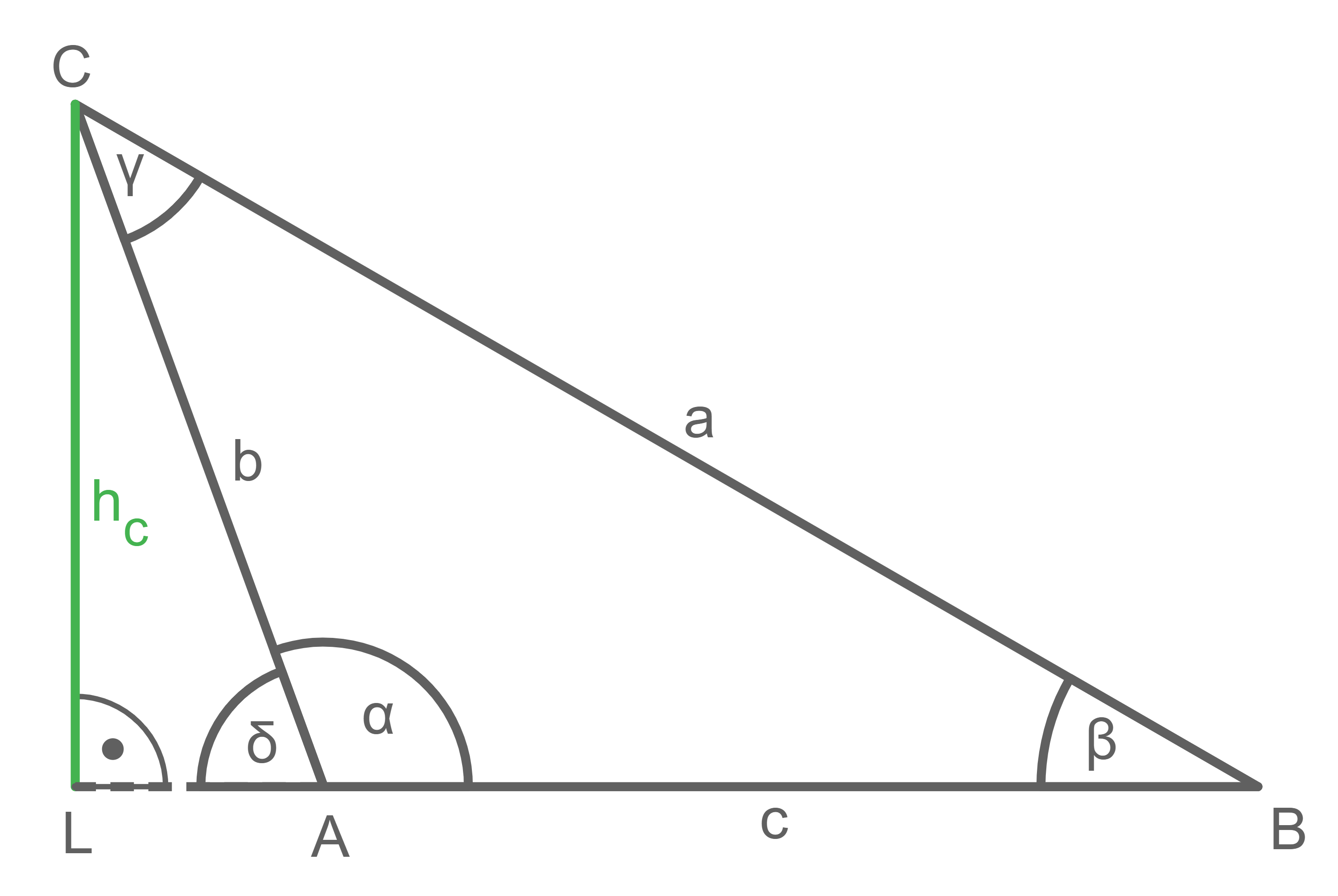Die Höhe $h_c$ liegt hier außerhalb des Dreiecks $ABC.$ Somit entstehen die beiden rechtwinkligen Dreiecke $LAC$ und $LBC.$ Die Grundseite des Dreiecks $LAC$ wird mit $c_1$ bezeichnet. Da $\delta=180^\circ-\alpha$ gilt, liefert das kleinere Teildreieck $\sin(180^\circ-\alpha)=\frac{h_c}{b}$ und $\cos(180^\circ-\alpha)=\frac{c_1}{b}.$
In dem größeren Teildreieck gilt $\sin(\beta)=\frac{h_c}{a}$ und $a^2={h_c}^2+{(c+c_1)}^2.$ Diese vier Gleichungen zusammen ergeben $\boldsymbol{\frac{a}{b}=\frac{\sin(180^\circ-\alpha)}{\sin(\beta)}}$ und $\boldsymbol{a^2=b^2+c^2+2bc\cdot\cos(180^\circ-\alpha)}.$

Umschreiben mit Hilfe der beiden Formeln vom Anfang liefert, dass die beiden erhaltenen Gleichungen für spitzwinklige Dreiecke die selben sind, wie die für stumpfwinklige Dreiecke. Analoge Überlegungen für die beiden Höhen $h_a$ und $h_b$ liefern zusammen den Sinussatz und Kosinussatz:

Sinussatz

$\dfrac{a}{b}=\dfrac{\sin(\alpha)}{\sin(\beta)}$
$\dfrac{b}{c}=\dfrac{\sin(\beta)}{\sin(\gamma)}$
$\dfrac{a}{c}=\dfrac{\sin(\alpha)}{\sin(\gamma)}$

Kosinussatz

$a^2=b^2+c^2-2bc\cdot\cos(\alpha)$
$b^2=a^2+c^2-2ac\cdot\cos(\beta)$
$c^2=a^2+b^2-2ab\cdot\cos(\gamma)$

Mit den Formeln des Sinussatzes lässt sich der Flächeninhalt von Dreiecken auch berechnen, wenn anstatt der Höhe zwei Seiten und der eingeschlossenen Winkel gegeben ist. In diesem Fall folgt, je nachdem welche Höhe durch die passende Formel ersetzt wird:

$A=\dfrac{1}{2}\cdot b\cdot c\cdot\sin(\alpha)$
$A=\dfrac{1}{2}\cdot a\cdot c\cdot\sin(\beta)$
$A=\dfrac{1}{2}\cdot a\cdot b\cdot\sin(\gamma)$

Der Sinussatz liefert:

$\begin{array}[t]{rll} \dfrac{a}{b}&=&\dfrac{\sin(\alpha)}{\sin(\beta)} \quad \scriptsize \mid\;\cdot b \\[5pt] a&=&\dfrac{\sin(\alpha)}{\sin(\beta)}\cdot b \quad \scriptsize \mid\;\cdot \frac{\sin(\beta)}{\sin(\alpha)} \\[5pt] a\cdot\dfrac{\sin(\beta)}{\sin(\alpha)}&=&b \\[5pt] 5,8\,\text{cm}\cdot\dfrac{\sin(55^\circ)}{\sin(65^\circ)}&=&b \\[5pt] 5,24\,\text{cm}&\approx&b \end{array}$

Mit der Winkelsumme folgt anschließend:

$\gamma=180^\circ-65^\circ-55^\circ=60^\circ$

Erneutes Anwenden des Sinussatzes liefert dann die letzte gesuchte Größe:

$\begin{array}[t]{rll} \dfrac{a}{c}&=&\dfrac{\sin(\alpha)}{\sin(\gamma)} \quad \scriptsize \mid\;\cdot c \\[5pt] a&=&\dfrac{\sin(\alpha)}{\sin(\gamma)}\cdot c \quad \scriptsize \mid\;\cdot \frac{\sin(\gamma)}{\sin(\alpha)} \\[5pt] a\cdot\dfrac{\sin(\gamma)}{\sin(\alpha)}&=&c \\[5pt] 5,8\,\text{cm}\cdot\dfrac{\sin(60^\circ)}{\sin(65^\circ)}&=&c \\[5pt] 5,54\,\text{cm}&\approx&c \end{array}$

Der Sinussatz liefert:

$\begin{array}[t]{rll} \dfrac{b}{c}&=&\dfrac{\sin(\beta)}{\sin(\gamma)} \quad \scriptsize \mid\;\cdot \sin(\gamma) \\[5pt] \dfrac{b}{c}\cdot \sin(\gamma)&=&\sin(\beta) \quad \scriptsize \mid\;\cdot \frac{c}{b} \\[5pt] \sin(\gamma)&=&\sin(\beta)\cdot\dfrac{c}{b} \\[5pt] \sin(\gamma)&=&\sin(25^\circ)\cdot\dfrac{8,2\,\text{cm}}{7,1\,\text{cm}} \\[5pt] \gamma&=&\sin^{-1}\left(\sin(25^\circ)\cdot\dfrac{8,2\,\text{cm}}{7,1\,\text{cm}}\right) \\[5pt] \gamma&\approx&29,2^\circ \end{array}$

Mit der Winkelsumme folgt anschließend:

$\alpha=180^\circ-25^\circ-29,2^\circ=125,8^\circ$

Erneutes Anwenden des Sinussatzes liefert dann die letzte gesuchte Größe:

$\begin{array}[t]{rll} \dfrac{a}{b}&=&\dfrac{\sin(\alpha)}{\sin(\beta)} \quad \scriptsize \mid\;\cdot b \\[5pt] a&=&\dfrac{\sin(\alpha)}{\sin(\beta)}\cdot b \\[5pt] a&=&\dfrac{\sin(125,8^\circ)}{\sin(25^\circ)}\cdot7,1\,\text{cm}\\[5pt] a&\approx&13,36\,\text{cm} \end{array}$

Der Sinussatz liefert:

$\begin{array}[t]{rll} \dfrac{a}{b}&=&\dfrac{\sin(\alpha)}{\sin(\beta)} \quad \scriptsize \mid\;\cdot \sin(\beta) \\[5pt] \dfrac{a}{b}\cdot \sin(\beta)&=&\sin(\alpha) \quad \scriptsize \mid\;\cdot \frac{b}{a} \\[5pt] \sin(\beta)&=&\sin(\alpha)\cdot\dfrac{b}{a} \\[5pt] \sin(\beta)&=&\sin(45^\circ)\cdot\dfrac{10,8\,\text{cm}}{8,2\,\text{cm}} \\[5pt] \beta&=&\sin^{-1}\left(\sin(45^\circ)\cdot\dfrac{10,8\,\text{cm}}{8,2\,\text{cm}}\right) \\[5pt] \beta&\approx&68,6^\circ \end{array}$

Mit der Winkelsumme folgt anschließend:

$\gamma = 180^\circ-45^\circ-68,6^\circ=66,4^\circ$

Erneutes Anwenden des Sinussatzes liefert dann die letzte gesuchte Größe:

$\begin{array}[t]{rll} \dfrac{a}{c}&=&\dfrac{\sin(\alpha)}{\sin(\gamma)} \quad \scriptsize \mid\;\cdot c \\[5pt] a&=&\dfrac{\sin(\alpha)}{\sin(\gamma)}\cdot c \quad \scriptsize \mid\;\cdot \frac{\sin(\gamma)}{\sin(\alpha)} \\[5pt] a\cdot\dfrac{\sin(\gamma)}{\sin(\alpha)}&=&c \\[5pt] 8,2\,\text{cm}\cdot\dfrac{\sin(66,4^\circ)}{\sin(45^\circ)}&=&c \\[5pt] 10,63\,\text{cm}&\approx&c \end{array}$