Potenzfunktionen mit natürlichen Exponenten
Eine Potenzfunktion n-ten Grades ist eine Funktion  mit
mit  wobei
wobei  und
und  eine natürliche Zahl größer als Null ist. Der Graph einer solchen Potenzfunktion wird im Fall
eine natürliche Zahl größer als Null ist. Der Graph einer solchen Potenzfunktion wird im Fall  Parabel n-ter Ordnung genannt.
Parabel n-ter Ordnung genannt.
 besitzen die Graphen der Potenzfunktionen einige allgemeine Eigenschaften, die oftmals nur davon abhängen, ob der Exponent gerade oder ungerade ist:
besitzen die Graphen der Potenzfunktionen einige allgemeine Eigenschaften, die oftmals nur davon abhängen, ob der Exponent gerade oder ungerade ist:
Der Graph jeder solchen Potenzfunktion verläuft durch den Ursprung  und den Punkt
und den Punkt 
Für gerade  ist der Graph achsensymmetrisch zur
ist der Graph achsensymmetrisch zur  -Achse.
-Achse.
Für ungerade  ist der Graph punktsymmetrisch zum Ursprung.
ist der Graph punktsymmetrisch zum Ursprung.
Für gerade  nimmt die Funktion nur die nicht-negativen reellen Zahlen an.
nimmt die Funktion nur die nicht-negativen reellen Zahlen an.
Für ungerade  nimmt die Funktion alle reellen Zahlen an.
nimmt die Funktion alle reellen Zahlen an.
 bewirkt der Parameter
bewirkt der Parameter  eine Verschiebung in bzw. gegen die
eine Verschiebung in bzw. gegen die  -Richtung und der Parameter
-Richtung und der Parameter  eine Verschiebung in bzw. gegen die
eine Verschiebung in bzw. gegen die  -Richtung. Der Paramter
-Richtung. Der Paramter  streckt bzw. staucht die Potenzfunktion.
streckt bzw. staucht die Potenzfunktion.
Eigenschaften
Im FallBeispiele
Gerades 
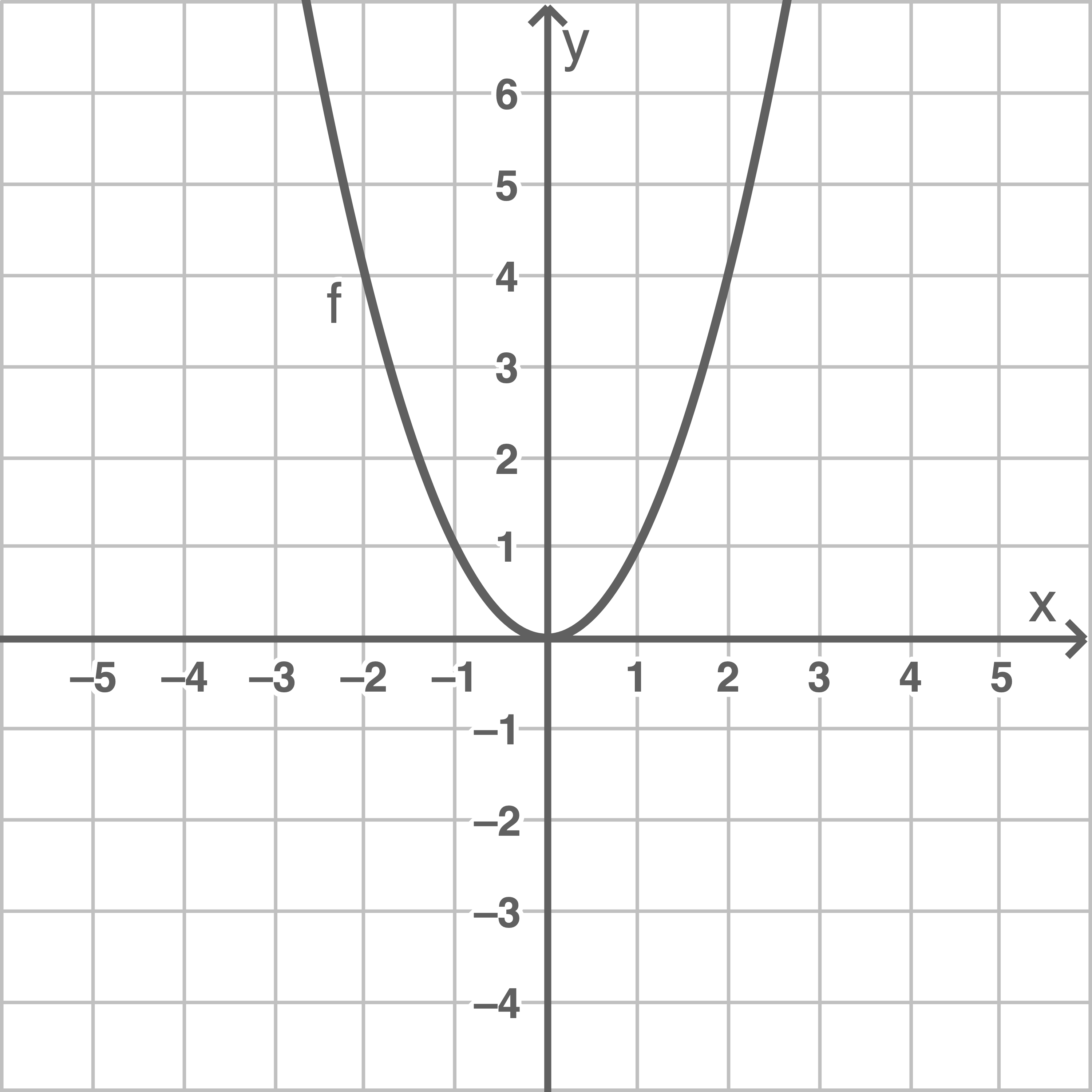


Ungerades 
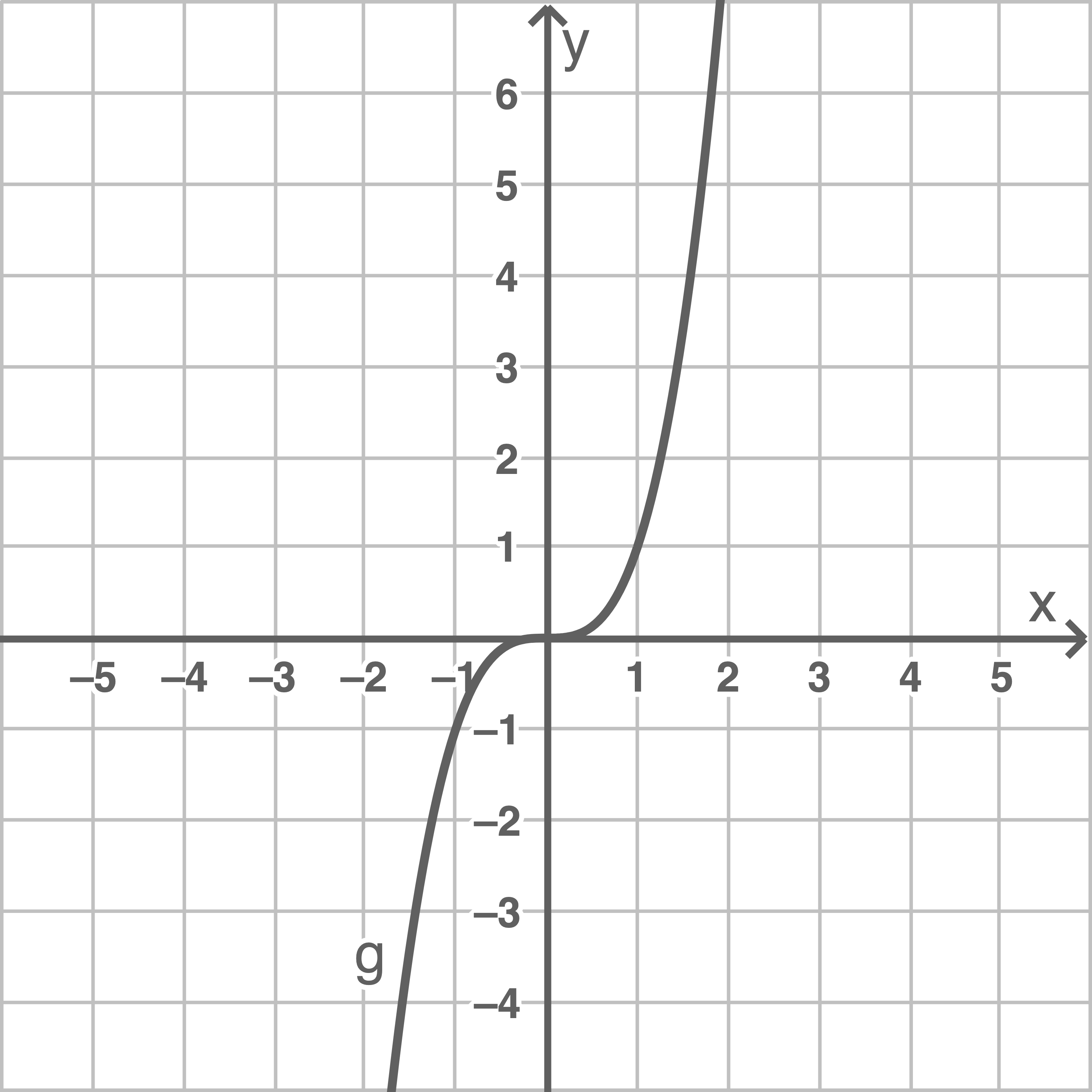

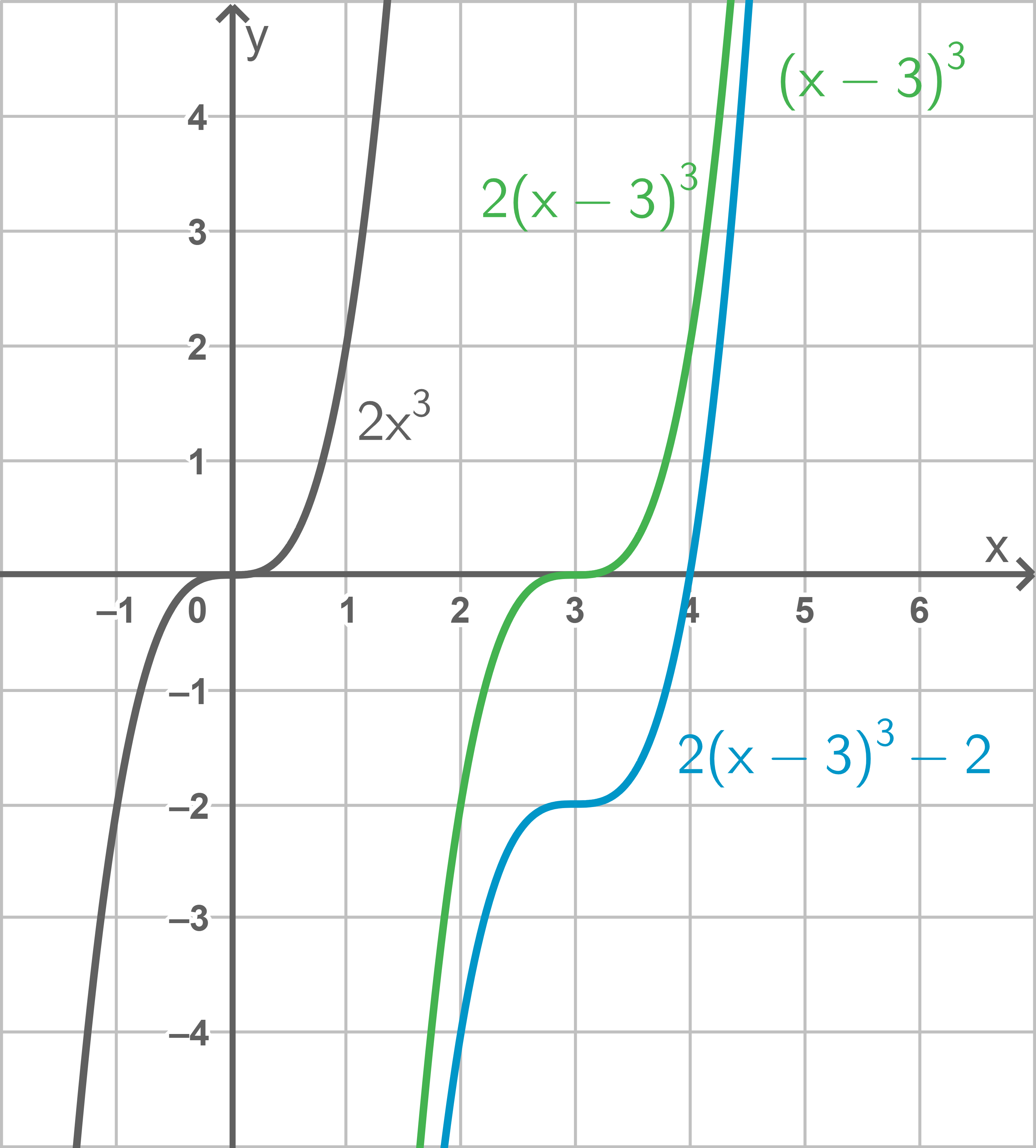
Die Graphen von Potenzfunktionen, sowohl mit geraden als auch mit ungeraden Exponenten, können durch Einfügen weiterer Parameter auch verschoben werden. In der Funktionsgleichung 

1
Gegeben ist die Potenzfunktion 
a)
Stelle eine Wertetabelle für den Bereich  in
in  er Schritten auf.
er Schritten auf.
b)
Zeichne den Graphen der Funktion mithilfe der Wertetabelle.
c)
Welche Symmetrie weist der Graph auf?
2
Es sind  und
und  gegeben. Zu beiden der folgenden Graphen gehört jeweils genau eine dieser vier Funktionsgleichungen. Ordne den Graphen die richtigen Gleichungen zu und erläutere deine Entscheidung.
gegeben. Zu beiden der folgenden Graphen gehört jeweils genau eine dieser vier Funktionsgleichungen. Ordne den Graphen die richtigen Gleichungen zu und erläutere deine Entscheidung.
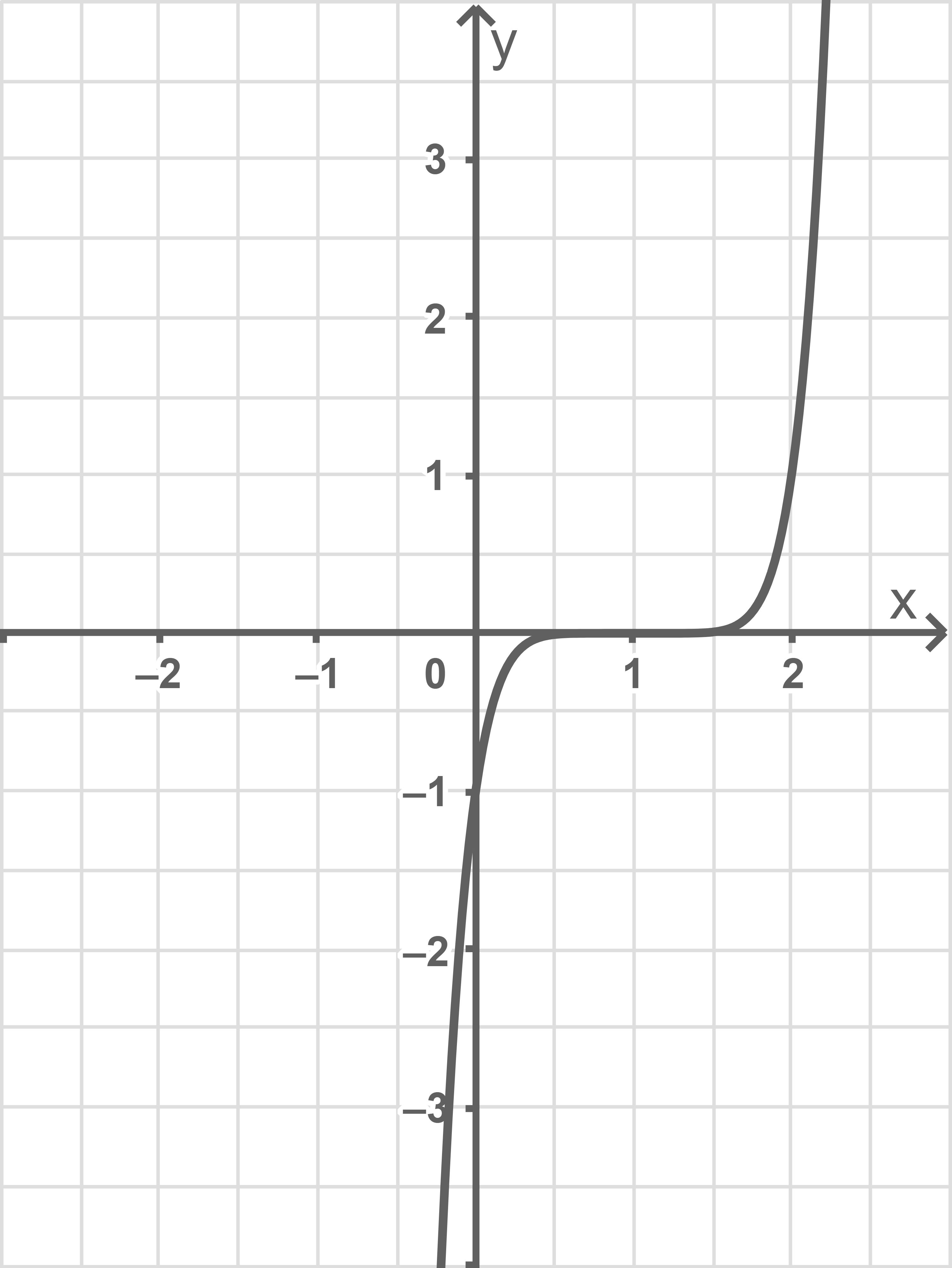

a)

b)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Einsetzen der  -Werte in die Funktionsgleichung der Potenzfunktion liefert:
-Werte in die Funktionsgleichung der Potenzfunktion liefert:
b)
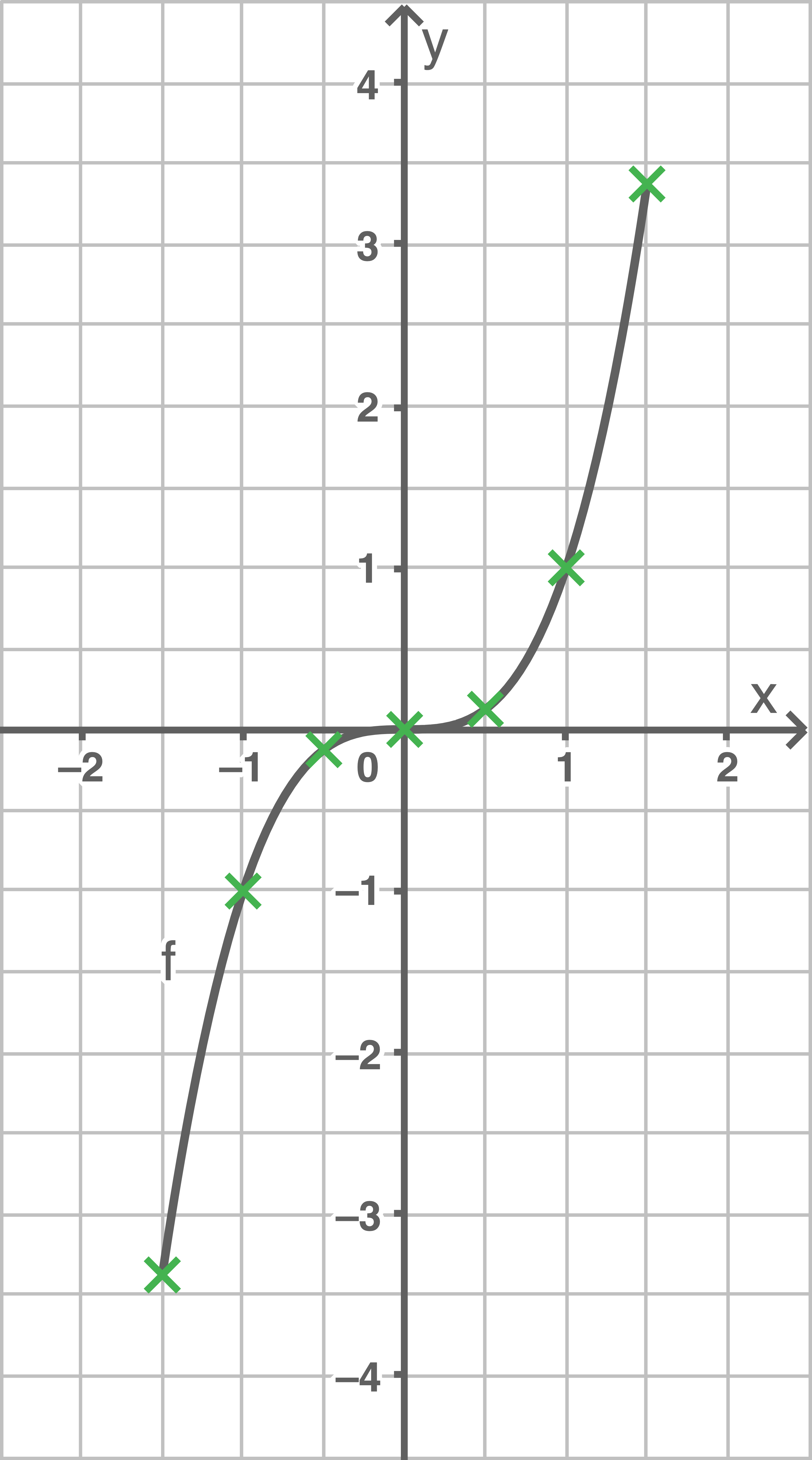
c)
Punktsymmetrie zum Ursprung
2
a)
Funktionsgleichung zuordnen
 Entscheidung erläutern
Der abgebildete Graph verläuft durch den Punkt
Entscheidung erläutern
Der abgebildete Graph verläuft durch den Punkt  und ist punktsymmetrisch zum Punkt
und ist punktsymmetrisch zum Punkt  Damit ist er eine Potenzfunktion ungeraden Grades mit Vorfaktor
Damit ist er eine Potenzfunktion ungeraden Grades mit Vorfaktor  die um eine Einheit in
die um eine Einheit in  -Richtung verschoben wurde. Die Funktionsgleichung von
-Richtung verschoben wurde. Die Funktionsgleichung von  gibt genau das an.
gibt genau das an.
b)
Funktionsgleichung zuordnen
 Entscheidung erläutern
Der abgebildete Graph verläuft durch die Punkte
Entscheidung erläutern
Der abgebildete Graph verläuft durch die Punkte  und
und  d.h. die zugehörige Funktionsgleichung besitzt den Vorfaktor
d.h. die zugehörige Funktionsgleichung besitzt den Vorfaktor  Zudem liegt der Graph für keinen
Zudem liegt der Graph für keinen  -Wert unterhalb der
-Wert unterhalb der  -Achse, sodass die zugrundeliegende Potenzfunktion einen geraden Exponenten besitzen muss. Somit kommt nur die Funktion
-Achse, sodass die zugrundeliegende Potenzfunktion einen geraden Exponenten besitzen muss. Somit kommt nur die Funktion  infrage.
infrage.