Sinus, Kosinus und Tangens
In einem rechtwinkligen Dreieck werden die drei Seiten des Dreiecks besonders bezeichnet, abhängig davon welcher Winkel des Dreiecks, außer der rechte Winkel, betrachtet wird. Die Seite des Dreiecks, die dem rechten Winkel gegenüber liegt, trägt immer den Namen Hypotenuse. Für den Winkel  ergeben sich die restlichen beiden Seiten wie folgt:
ergeben sich die restlichen beiden Seiten wie folgt:
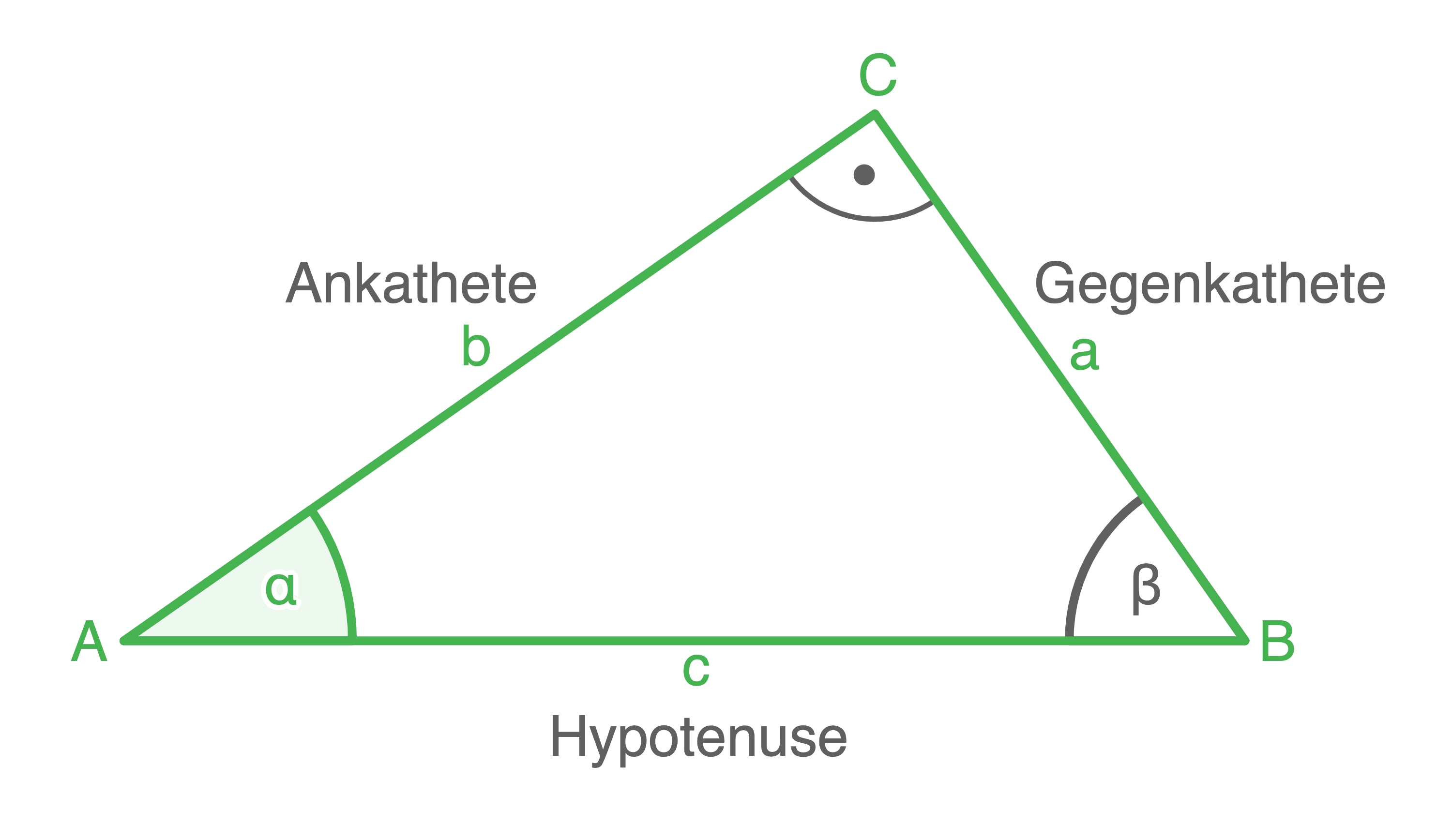 Die Seiten eines rechtwinkligen Dreiecks werden somit aus der Hypotenuse und zwei Katheten gebildet.
Die Seiten eines rechtwinkligen Dreiecks werden somit aus der Hypotenuse und zwei Katheten gebildet.
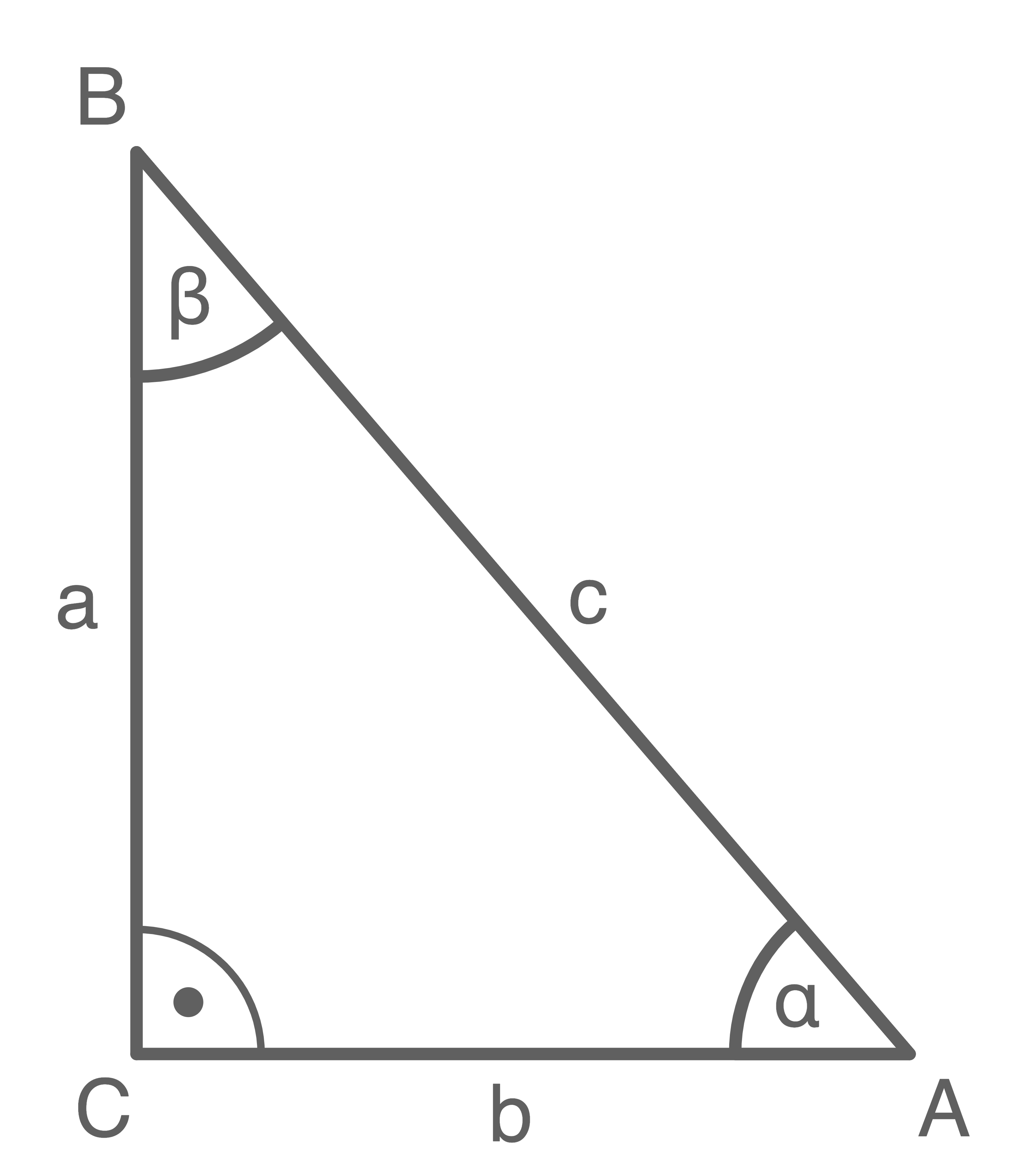
Mit Hilfe dieser Begriffe werden Sinus, Kosinus und Tangens definiert, mit denen Berechnungen an rechtwinkligen Dreiecken durchgeführt werden können: gelten die entsprechenden Bezeichnungen der Seiten und Sinus, Kosinus sowie Tangens sind dementsprechend definiert.
gelten die entsprechenden Bezeichnungen der Seiten und Sinus, Kosinus sowie Tangens sind dementsprechend definiert.
 Die Werte
Die Werte  bzw.
bzw.  geben die Länge der Gegenkathete bzw. Ankathete von
geben die Länge der Gegenkathete bzw. Ankathete von  an. Mit diesen beiden Werten kann die Größe des Winkels
an. Mit diesen beiden Werten kann die Größe des Winkels  über den Tangens bestimmt werden:
über den Tangens bestimmt werden:
![\(\begin{array}[t]{rlll}
\tan(\alpha)&=&\dfrac{a}{b} \\[5pt]
\tan(\alpha)&=&\dfrac{4,5\,\text{cm}}{5,2\,\text{cm}} \\[5pt]
\tan(\alpha)&=&\dfrac{4,5}{5,2} &\mid\;\tan^{-1} \\[5pt]
\alpha&=&\tan^{-1}\left(\dfrac{4,5}{5,2}\right)\\[5pt]
\alpha&\approx&40,87^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/beabcfe36ff091367f2294f8e02a2743866f2bc3d6f1560c5a81fac754f3db85_light.svg)
- Die Ankathete von
ist die Seite im Dreieck, die, zusätzlich zur Hypotenuse, ebenfalls am Winkel
anliegt.
- Die Gegenkathete von
ist die Seite im Dreieck, die dem Winkel
gegenüber liegt.

Mit Hilfe dieser Begriffe werden Sinus, Kosinus und Tangens definiert, mit denen Berechnungen an rechtwinkligen Dreiecken durchgeführt werden können:
Beispiel
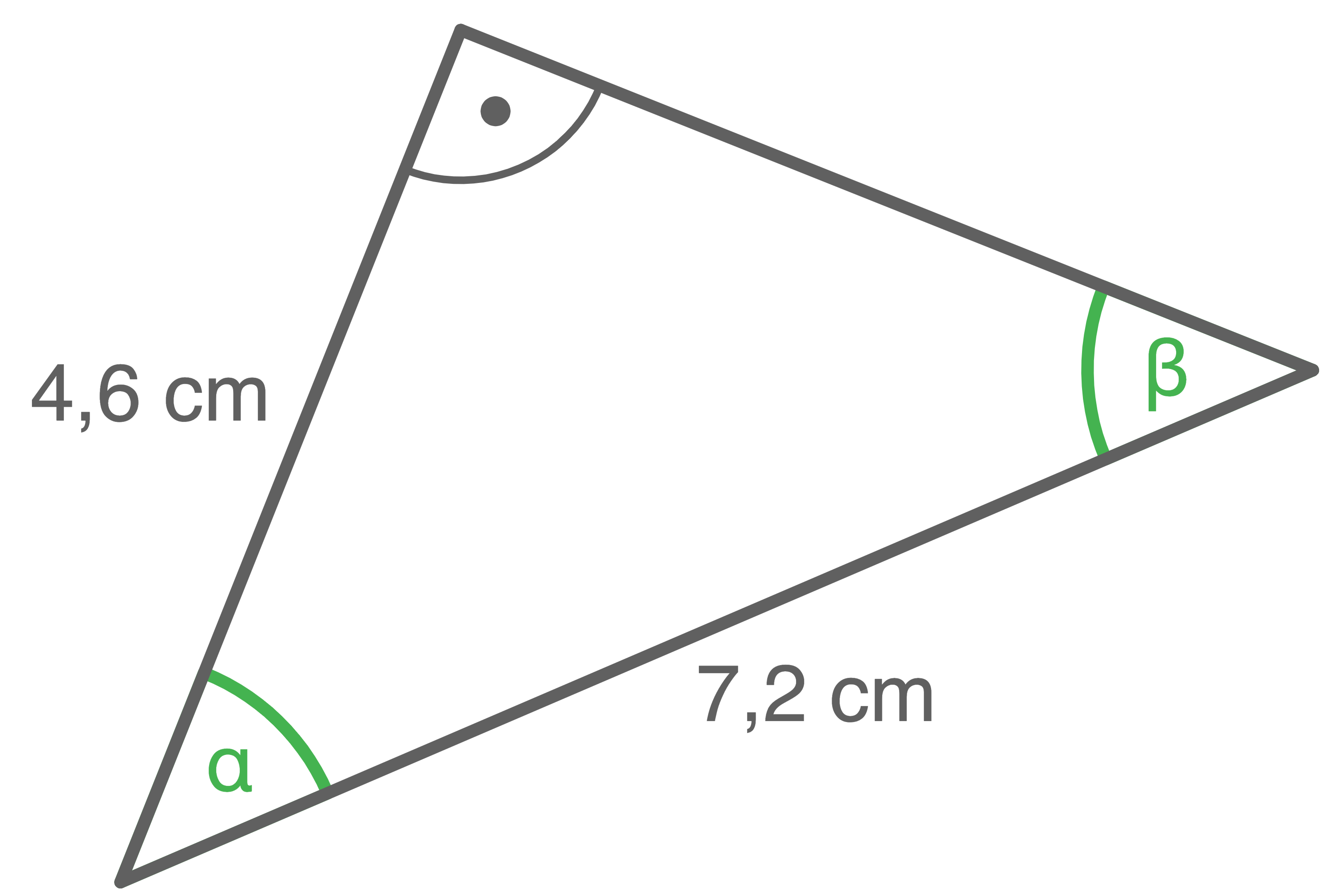
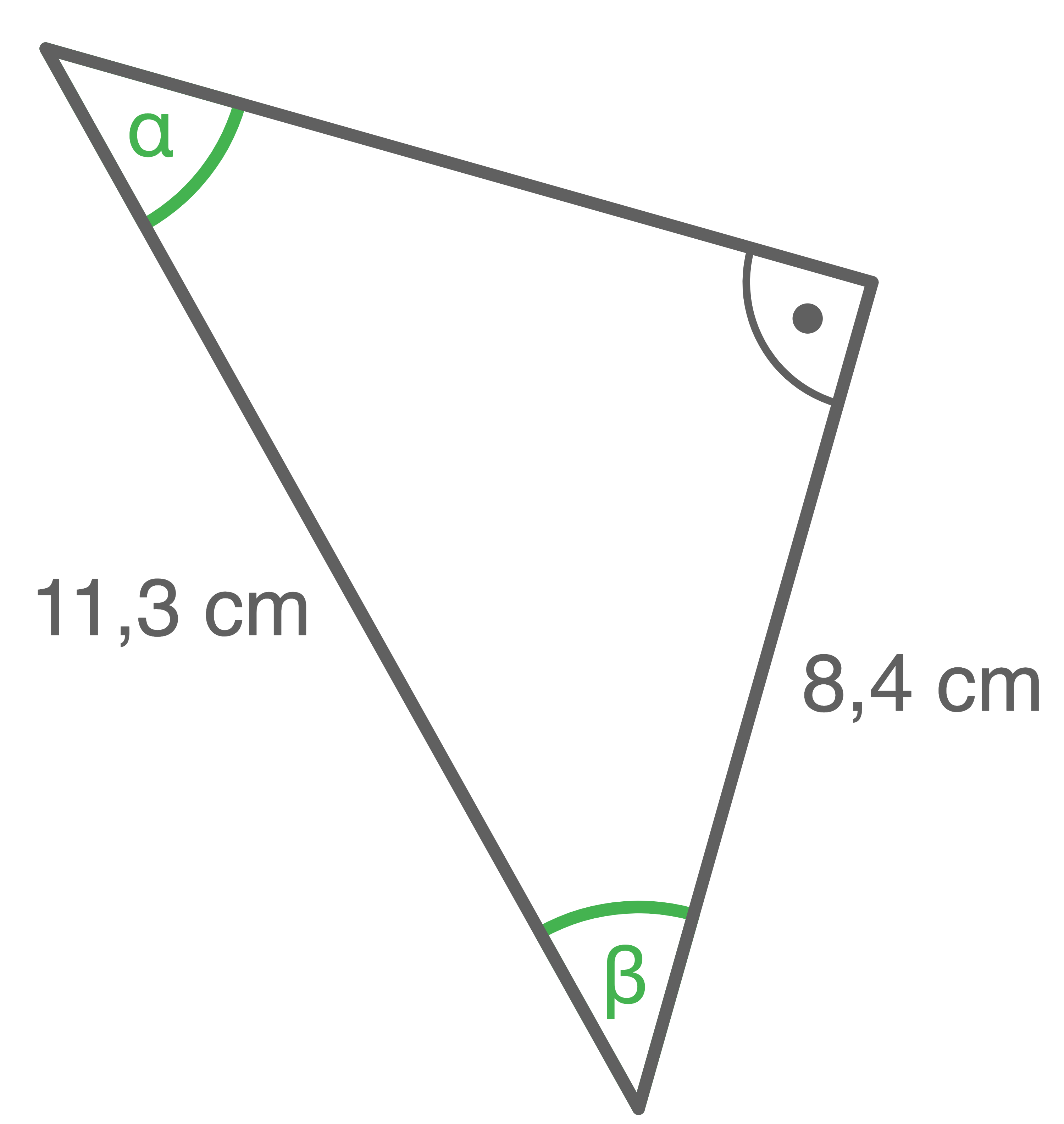
Von dem abgebildeten Dreieck sind die folgenden beiden Seitenlängen bekannt:


1
Berechne die Größe der markierten Winkel.
a)

b)

c)

d)

2
Mia möchte eine Fahrradtour in den Bergen machen. Als sie an ihrem Startpunkt ankommt, sieht sie das abgebildete Verkehrsschild am Straßenrand stehen. Berechne die Strecke, die Mia mit dem Fahrrad fährt, wenn sie insgesamt  Höhenmeter zurücklegt und davon ausgegangen wird, dass die Straße sowohl immer die gleiche Steigung als auch keine Kurven besitzt.
Höhenmeter zurücklegt und davon ausgegangen wird, dass die Straße sowohl immer die gleiche Steigung als auch keine Kurven besitzt.

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
1. Schritt: Größe des Winkels  berechnen
Die Länge der Ankathete von
berechnen
Die Länge der Ankathete von  und der Hypotenuse sind gegeben. Somit folgt:
und der Hypotenuse sind gegeben. Somit folgt:
![\(\begin{array}[t]{rll}
\cos(\alpha) &=&\dfrac{4,6\,\text{cm}}{7,2\,\text{cm}} \\[5pt]
\cos(\alpha) &=&\dfrac{4,6}{7,2} &\quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\alpha &=&\cos^{-1}\left(\dfrac{4,6}{7,2}\right) \\[5pt]
\alpha &\approx& 50,29^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d9afd3b97fa26e59c96eda3603e10b4ed64d210f33ab765d253d318d062d09b4_light.svg) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer
berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer  beträgt, folgt:
beträgt, folgt:
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-\alpha-90^{\circ} \\[5pt]
&\approx& 180^{\circ}-50,29^{\circ}-90^{\circ} \\[5pt]
&=& 39,71^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/b0ff64292e379b3357f5ec01bfbf1af8264c3641b05ec589718f895cb6f24f2e_light.svg)
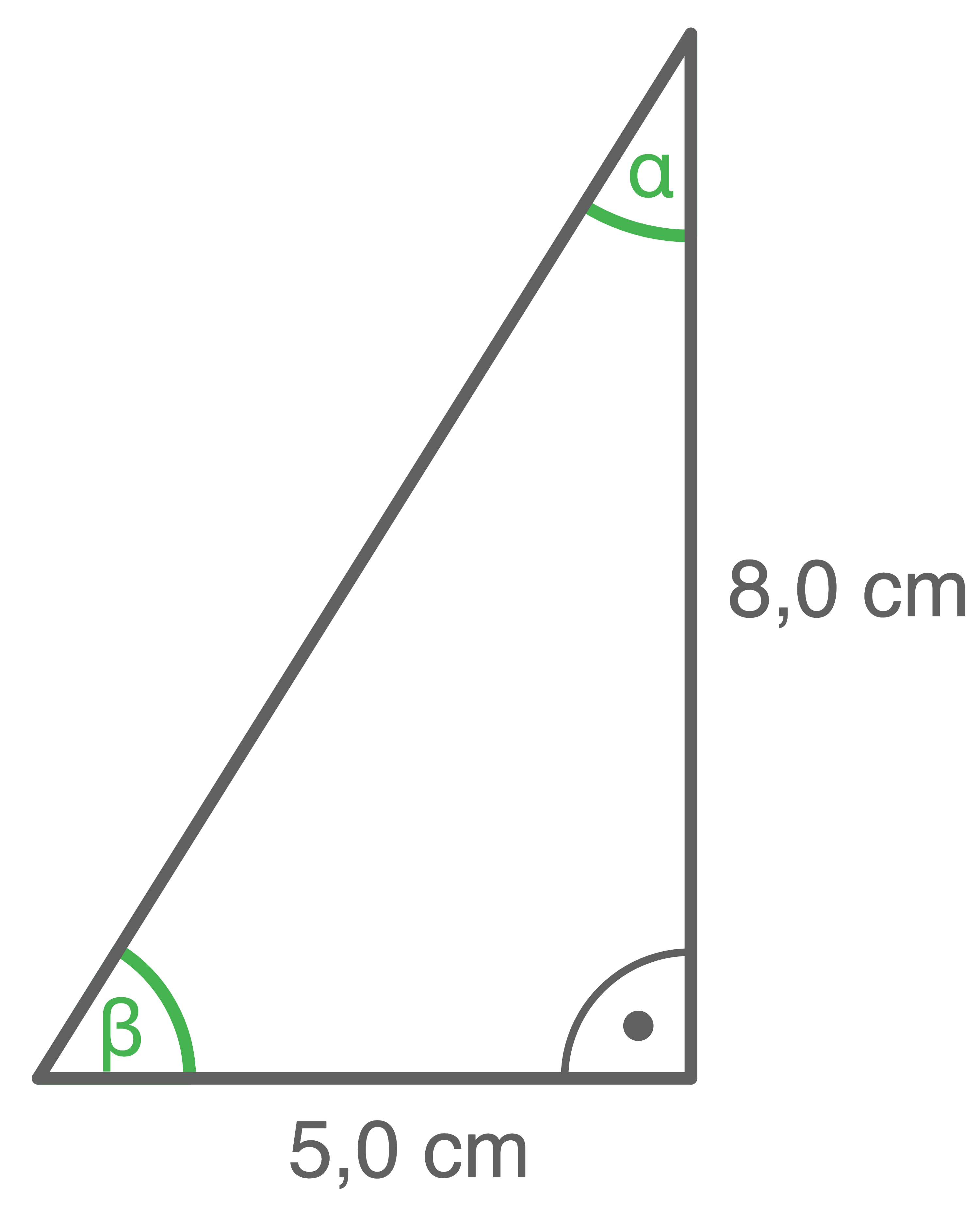
b)
1. Schritt: Größe des Winkels  berechnen
Die Länge der Ankathete und der Gegenkathete von
berechnen
Die Länge der Ankathete und der Gegenkathete von  sind gegeben. Somit folgt:
sind gegeben. Somit folgt:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{5,0\,\text{cm}}{8,0\,\text{cm}} \\[5pt]
\tan(\alpha)&=&\dfrac{5,0}{8,0} &\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha &=&\tan^{-1}\left(\dfrac{5,0}{8,0}\right) \\[5pt]
\alpha&\approx&32,01^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c4f6951564bcbd1f470846ad49eb8789f5c4fb4efeae74442b0a9e31fa1a9e58_light.svg) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer
berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer  beträgt, folgt:
beträgt, folgt:
![\(\begin{array}[t]{rll}
\beta&=&180^{\circ}-\alpha-90^{\circ} \\[5pt]
&\approx&180^{\circ}-32,01^{\circ}-90^{\circ} \\[5pt]
&=&57,99^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/f1ac08cd82d1f43c1335a738da7ae00b921c7aaa5a59fbe570455e48238f463c_light.svg)
c)
1. Schritt: Größe des Winkels  berechnen
Die Länge der Gegenkathete von
berechnen
Die Länge der Gegenkathete von  und der Hypotenuse sind gegeben. Somit folgt:
und der Hypotenuse sind gegeben. Somit folgt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{8,4\,\text{cm}}{11,3\,\text{cm}} \\[5pt]
\sin(\alpha)&=&\dfrac{8,4}{11,3} &\quad \scriptsize \mid\; \sin^{-1} \\[5pt]
\alpha &=&\sin^{-1}\left(\dfrac{8,4}{11,3}\right) \\[5pt]
\alpha&\approx&48,02^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/53c4a7d3eabcd57591efe9b5e498c77ccfc389ffc2add8b48b8260a7ba3c88a1_light.svg) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer
berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer  beträgt, folgt:
beträgt, folgt:
![\(\begin{array}[t]{rll}
\beta&=&180^{\circ}-\alpha-90^{\circ} \\[5pt]
&\approx&180^{\circ}-48,02^{\circ}-90^{\circ} \\[5pt]
&=&41,98^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/fb0cd74ce4b43caa5c4f5a93b50354ce5ca3e3551156792bc310d8ef39bcb011_light.svg)
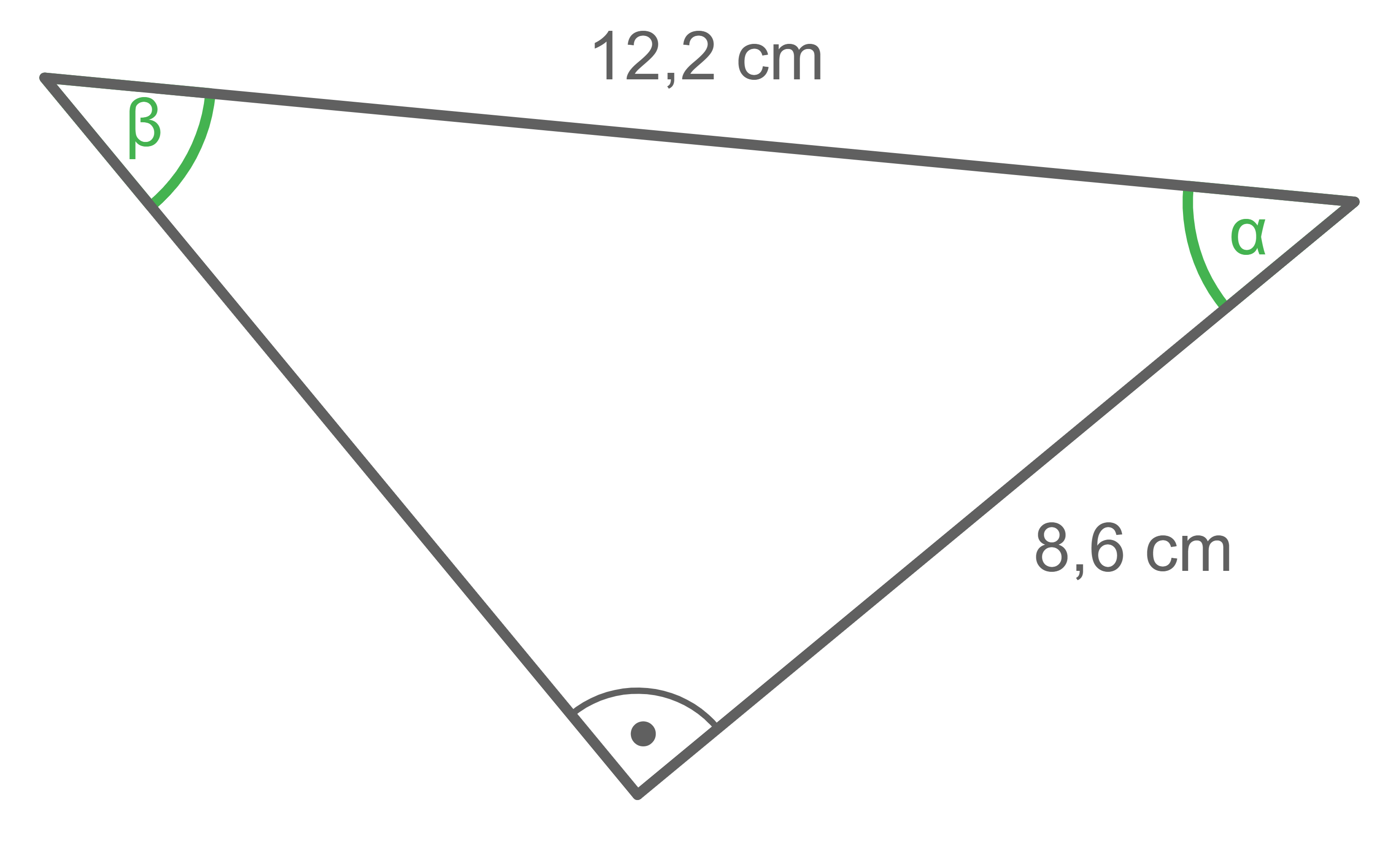
d)
1. Schritt: Größe des Winkels  berechnen
Die Länge der Ankathete von
berechnen
Die Länge der Ankathete von  und der Hypotenuse sind gegeben. Somit folgt:
und der Hypotenuse sind gegeben. Somit folgt:
![\(\begin{array}[t]{rll}
\cos(\alpha) &=&\dfrac{8,6\,\text{cm}}{12,2\,\text{cm}} \\[5pt]
\cos(\alpha) &=&\dfrac{8,6}{12,2} &\quad \scriptsize \mid\; \cos^{-1} \\[5pt]
\alpha &=&\cos^{-1}\left(\dfrac{8,6}{12,2}\right) \\[5pt]
\alpha &\approx& 45,18^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a5facc66f43b198902431b75b763eb7a7d923d40fcaf1dbe232f03ba8fa8982c_light.svg) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer
berechnen
Mit der Innenwinkelsumme eines Dreiecks, die immer  beträgt, folgt:
beträgt, folgt:
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-\alpha-90^{\circ} \\[5pt]
&\approx& 180^{\circ}-45,18^{\circ}-90^{\circ} \\[5pt]
&=& 44,82^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/3210400925cb1a5183ff71f8f279c5875edabaa0b66706a0a4c8dab9dfa2a525_light.svg)
2
Mit Hilfe des Hinweises und  ergibt sich folgender Neigungswinkel:
ergibt sich folgender Neigungswinkel:
![\(\begin{array}[t]{rlll}
\alpha&=&1,2\cdot6^\circ \\[5pt]
&=&7,2^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/34f99dbefe493e35ec82b1933467316bb83071f60871eb4f25c41812721624c4_light.svg) Der Sachverhalt kann nun in einem rechtwinkligen Dreieck aufgetragen werden. Hierbei wird die Höhe von
Der Sachverhalt kann nun in einem rechtwinkligen Dreieck aufgetragen werden. Hierbei wird die Höhe von  Metern orthogonal zur Grundseite aufgetragen. Die gesuchte Länge
Metern orthogonal zur Grundseite aufgetragen. Die gesuchte Länge  der Strecke, die Mia zurücklegt, ist somit durch die Länge der Hypothenuse gegeben. Da die Höhe die Länge der Gegenkatheten des Steigungswinkels
der Strecke, die Mia zurücklegt, ist somit durch die Länge der Hypothenuse gegeben. Da die Höhe die Länge der Gegenkatheten des Steigungswinkels  angibt, muss der Sinus angewendet werden:
angibt, muss der Sinus angewendet werden:
![\(\begin{array}[t]{rlll}
\sin(\alpha)&=&\dfrac{100\,\text{m}}{\ell} &\mid\;\cdot\ell \\[5pt]
\sin(7,2^\circ)\cdot\ell&=&100\,\text{m} &\mid\;:\sin(7,2^\circ) \\[5pt]
\ell&=&\dfrac{100\,\text{m}}{\sin(7,2^\circ)} \\[5pt]
\ell&=&800\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/5612d8104f45e3f4f72974db0097d274d58c86cb9ea932249e3c8b695488b694_light.svg)