Trigonometrie anwenden
In vielen Körpern, Figuren und Objekten aus dem Alltag lassen sich Teildreiecke wiederfinden. Mit Hilfe der trigonometrischen Funktionen Sinus, Kosinus und Tangens, sowie der Innenwinkelsumme eines Dreiecks und des Sinus- bzw. Kosinussatzes, lassen sich aus wenigen bekannten Informationen die restlichen Größen dieser Teildreiecke bestimmen. Dabei wird in mehreren Schritten vorgegangen:
Gegeben sind der Winkel im Eckpunkt 
sowie der Winkel zwischen der Diagonalen 
und der Strecker 
sowie die Länge der Diagonalen 
Gesucht sind die Winkel in den restlichen drei Eckpunkten
und 
sowie alle Seitenlängen.
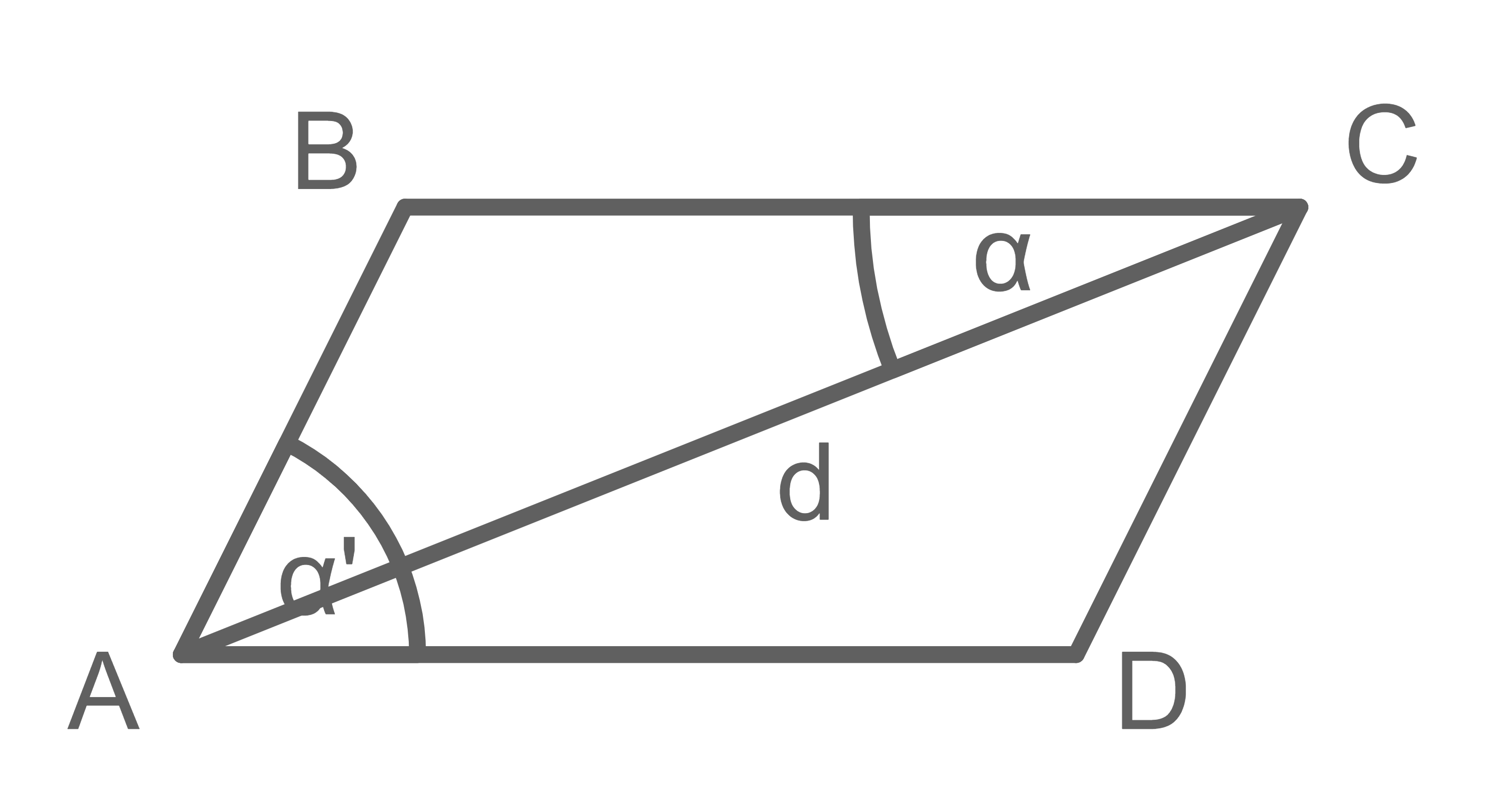
Die Diagonale teilt das Parallelogramm in zwei identische Dreiecke. Der Winkel 
ist aus Symmetriegründen somit gerade der Winkel im Punkt 
des entstandenen Dreiecks 
In einem Parallelogramm sind, da gegenüberliegende Seiten stets parallel sind, auch die gegenüberliegenden Winkel gleichgroß. Der Winkel 
des Dreiecks 
im Eckpunkt 
wird somit wie folgt erhalten:
Damit kann nun die Regel wsw auf das Dreieck angewendet werden, um die restlichen Seitenlängen und Winkel zu bestimmen.
Mit Hilfe der Innenwinkelsumme folgt zunächst:
Der Sinussatz liefert dann die beiden verbliebenen Seitenlängen:
![\(\begin{array}[t]{rlll}
\dfrac{a}{d}&=&\dfrac{\sin(\alpha)}{\sin(\delta)} &\mid\;\cdot d \\[5pt]
a&=&\dfrac{\sin(\alpha)}{\sin(\delta)}\cdot d \\[5pt]
a&=&\dfrac{\sin(25^\circ)}{\sin(105^\circ)}\cdot 10\;\text{cm} \\[5pt]
a&\approx&4,38\;\text{cm}
\end{array}\)](https://mathjax.schullv.de/37e7da283ae47db943179884fce80b7b68d6cf3af8abe9b7562dfd0da572a9c0?color=5a5a5a)
![\(\begin{array}[t]{rlll}
\dfrac{c}{d}&=&\dfrac{\sin(\gamma)}{\sin(\delta)} &\mid\;\cdot d \\[5pt]
c&=&\dfrac{\sin(\gamma)}{\sin(\delta)}\cdot d \\[5pt]
c&=&\dfrac{\sin(50^\circ)}{\sin(105^\circ)}\cdot 10\;\text{cm} \\[5pt]
c&\approx&7,93\;\text{cm}
\end{array}\)](https://mathjax.schullv.de/f790c1beec82080a7e3673cc9c0d19b43d10c2cf2f54962d385c5597f0b7f97f?color=5a5a5a)
Aufgrund der Symmetrien eines Parallelogramms sind somit nun alle WInkel und Seitenlängen bekannt. Die Winkel bei und betragen jeweils 
die bei 
und 
jeweils 
Das Parallelogramm besitzt zudem zwei Seiten der Länge 
sowie zwei mit der Länge 
- Aufstellen der gegebenen und gesuchten Werte
- Teildreiecke erkennen, gegebenenfalls mit Hilfe einer Skizze
- Trigonometrische Funktionen, Innenwinkelsumme und Sinus- und Kosinussatz verwenden, um die fehlenden Größen zu berechnen
Beispiel
Von dem abgebildeten Parallelogramm sind die beiden Winkel 
und 
bekannt, sowie die Länge 
der Diagonalen. Bestimme die Seitenlängen des Parallelogramms und die Innenwinkel in allen vier Eckpunkten.
Gesucht sind die Winkel in den restlichen drei Eckpunkten
Mit Hilfe der Innenwinkelsumme folgt zunächst:
1
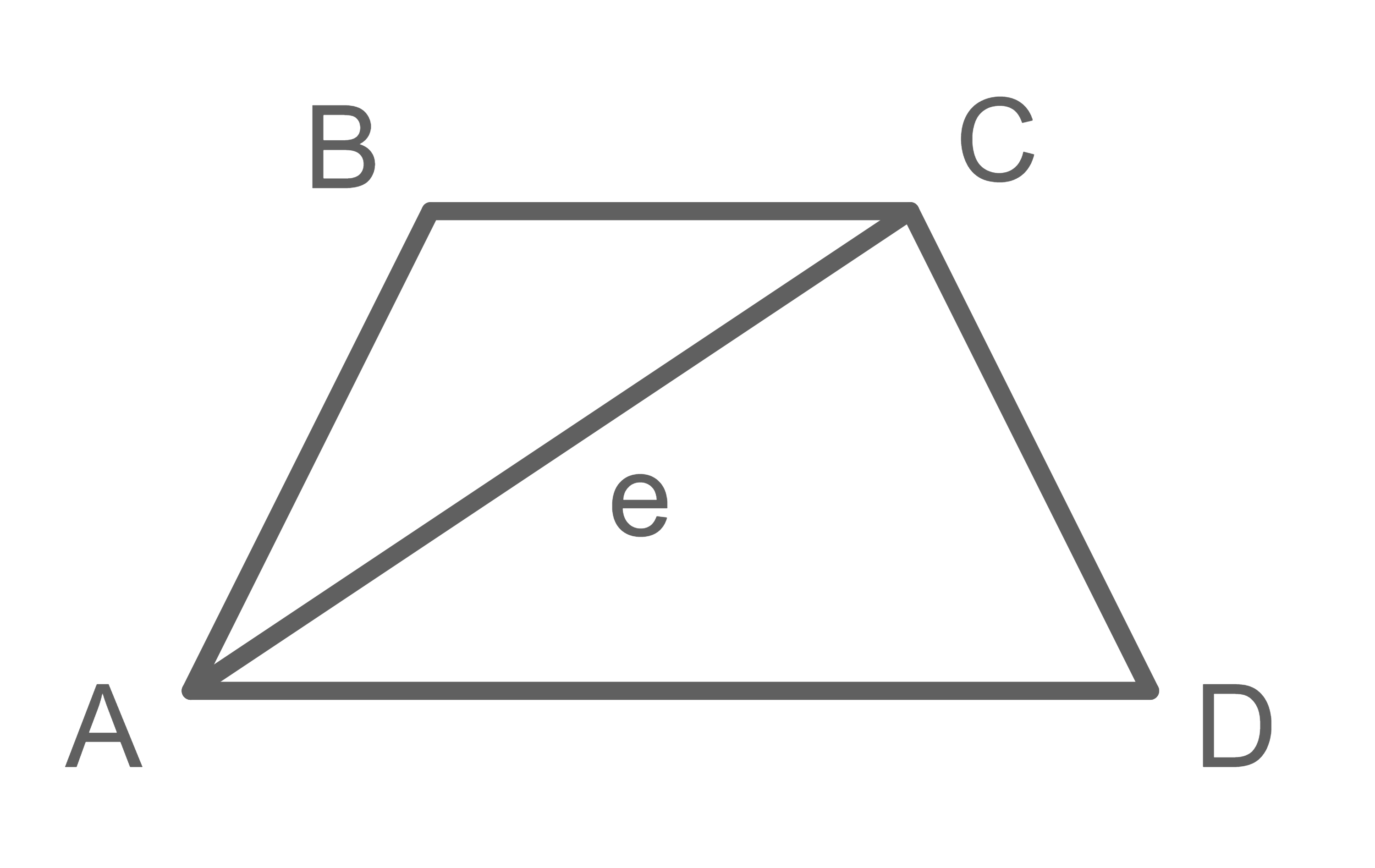
Eine Schule hat neue Sitzmöbel für ihren Eingangsbereich bestellt. Ein Querschnitt von einem dieser ist hier abgebildet. Bekannt sind die Maße 
der Diagonalen, sowie, dass die Unterseite 
und die Oberseite 
breit ist.
Bestimme die Höhe der von der Schule bestellten Sitzmöbel.
Bestimme die Höhe der von der Schule bestellten Sitzmöbel.
2
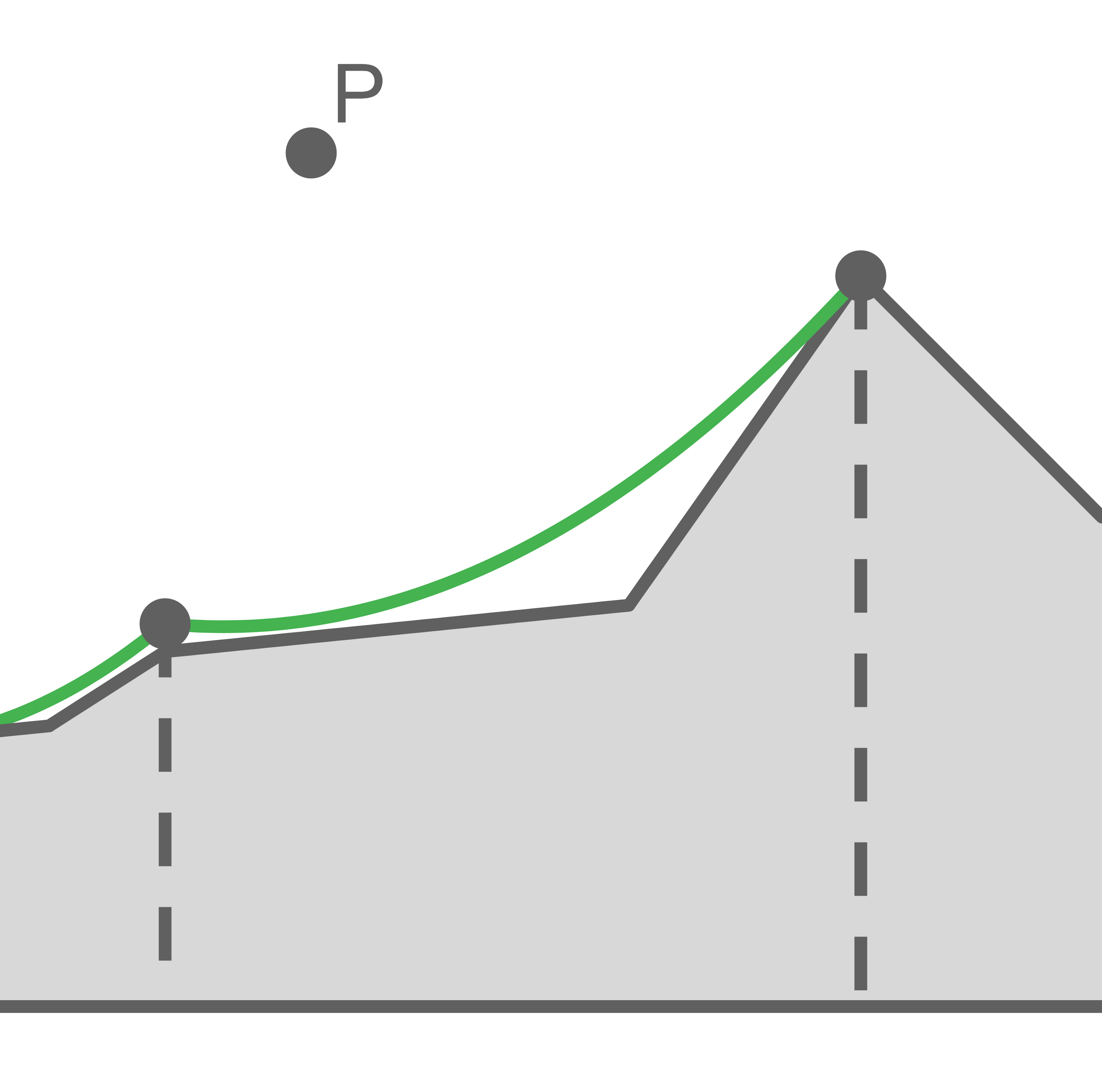
Ein Seilbahnunternehmen möchte spektakuläre Bilder ihres Betriebs machen. Dazu stationieren sie eine Drohne im Punkt 
in der Luft über dem obersten Abschnitt der Seilbahn. Diese ist mit Kameras ausgestattet, die auf die beiden abgebildeten Stationen gerichtet sind, und ist Luftlinie 
von der unteren Station sowie 
von der oberen entfernt. Die beiden Seilbahnstationen liegen Luftlinie 
auseinander.
Um welchen Winkel müssen Besucher, die auf einer der Stationen sind und zur anderen herüberblicken, ihren Kopf jeweils drehen, um direkt in die jeweilige Kamera der Drone zu schauen?
Um welchen Winkel müssen Besucher, die auf einer der Stationen sind und zur anderen herüberblicken, ihren Kopf jeweils drehen, um direkt in die jeweilige Kamera der Drone zu schauen?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Gegeben sind die Maße der Unter- sowie Oberseite des symmetrischen Trapezes und der Diagonalen 
Gesucht wird die Höhe 
des Trapezes.
Einzeichnen der Trapezhöhe durch den Punkt liefert ein rechtwinkliges Dreieck:
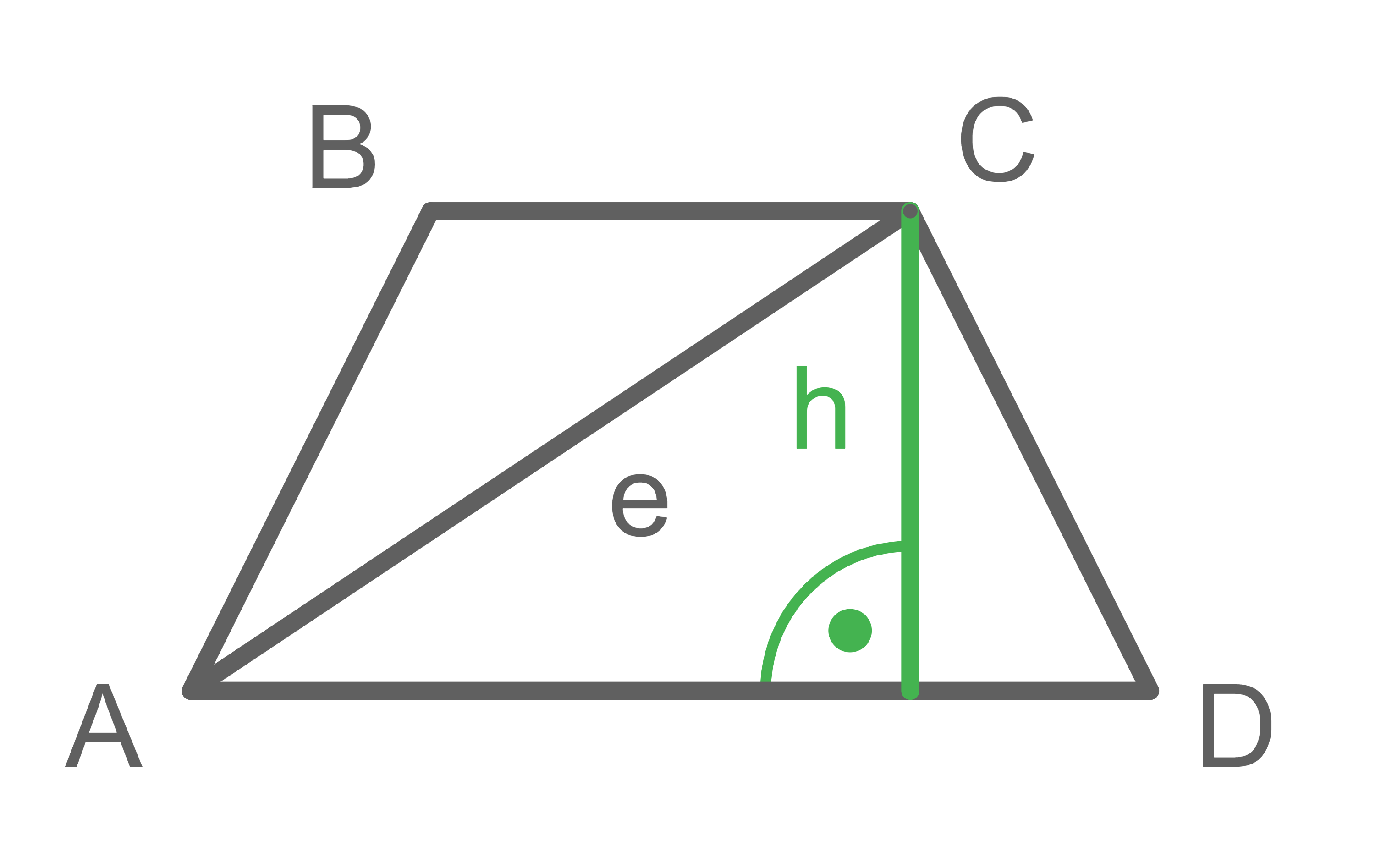Die Grundseite 
dieses Dreiecks lässt sich mit Hilfe der bekannten Längen der Ober- bzw. Unterseite des Trapezes bestimmen:
![\(\begin{array}[t]{rlll}
a&=&2\;\text{m}-\dfrac{1}{2}\cdot(2\;\text{m}-1,25\;\text{m}) \\[5pt]
&=&2\;\text{m}-0,375\;\text{m} \\[5pt]
&=&1,625\;\text{m}
\end{array}\)](https://mathjax.schullv.de/62aeb48069fa0a6d73cb22fd586fbe5ddc1f758532a40cb61553ea33498047c2?color=5a5a5a)
Um die Höhe zu erhalten, wird zunächst die Größe einer der beiden verbliebenen Dreieckswinkel benötigt. Für die des Winkels im Punkt folgt z.B.:
![\(\begin{array}[t]{rlll}
\cos(\alpha)&=&\dfrac{1,625\;\text{m}}{1,7\;\text{m}} \\[5pt]
\alpha&=&\cos^{-1}\left(\dfrac{1,625}{1,7}\right) \\[5pt]
\alpha&\approx&17,08^\circ
\end{array}\)](https://mathjax.schullv.de/3d9facf9cdd04723397d65c729e9afdfb7037d735c5704d6ebe881bd950ad53e?color=5a5a5a)
Für die Höhe folgt nun mit dem Sinus:
Die bestellten Sitzmöbel besitzen somit eine Höhe von ca. 
2
Gegeben sind die Entfernungen der Drohe von den beiden Seilbahnstationen, sowie der Abstand dieser beiden zueinander. Gesucht sind die Winkel, um die die Besucher der Stationen jeweils ihren Kopf drehen müssen, um in die Kameras der Drohne zu schauen.
Die Drone bildet zusammen mit den beiden Seilbahnstationen ein Dreieck:
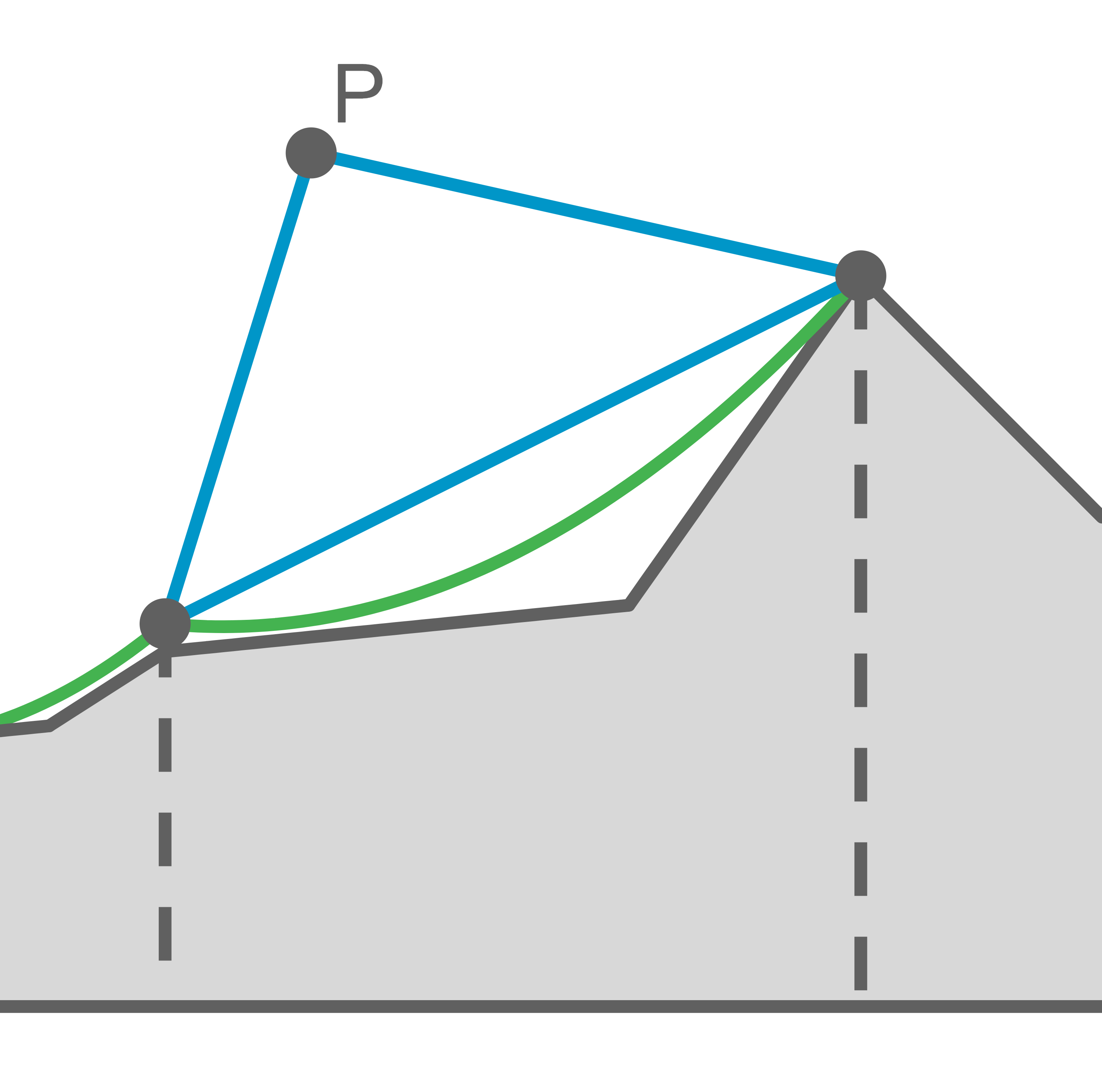Die beiden gesuchten Winkel sind in diesem Zusammenhang durch die Innenwinkel des Dreiecks an den Stationen gegeben. Für den Winkel der unteren Station folgt mit dem Kosinussatz:
Für den Winkel der oberen Station ergibt sich mit dem Sinussatz:
Die Besucher auf der oberen Seilbahnstation müssen ihre Köpfe somit um ca. 
drehen, während die Besucher auf der unteren Station ihre Köpfe um ca. 
drehen müssen.
Abbildung 1