Aufgabe 1A

Der Sprung eines Fallschirmspringers soll in drei Phasen modelliert werden. In Phase A, beginnend zum Zeitpunkt $t_{0}=0$ , wird der Springer bei geschlossenem Fallschirm immer schneller. In Phase B fällt er aufgrund des Luftwiderstandes mit konstanter Sinkgeschwindigkeit. Mit Öffnen des Fallschirms soll Phase C beginnen, in der der Fallschirm den Springer zunächst deutlich abbremst, so dass er schließlich eine zum Landen geeignete nahezu konstante Sinkgeschwindigkeit erreicht. Während des gesamten Sprungs werden die Höhe in Metern über dem Boden und die Zeit in Sekunden gemessen.

a) In Phase B soll der Fallschirmsprung durch die Funktion $h_B$ mit $h_{B}(t)=1.500-50\cdot t$ modelliert werden.
Bestimmen Sie die Sinkgeschwindigkeit des Fallschirmspringers in Phase B.
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion $h_{A}$ mit $h_A(t)=a\cdot t^{2}+b\cdot t+c$ modelliert werden. Diese soll zum Zeitpunkt $t_{1}=8\,\text{s}$ stetig und differenzierbar an $h_{B}$ anschließen. Ihr Graph soll durch den Punkt $(4\mid1.250)$ verlaufen.
Bestimmen Sie mithilfe dieser Informationen die Funktionsgleichung für $h_A$ .

(11P)

b) Abbildung 1 der Anlage zeigt die Höhe $h$ des Springers in Abhängigkeit von der Zeit $t$ .
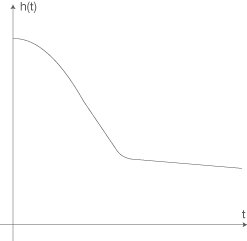
Geben Sie die Grenzen der Phasen A, B und C näherungsweise an, indem Sie diese in der Abbildung 1 markieren und die Abschnitte beschriften.
In der Abbildung 2 der Anlage ist der Graph der Sinkgeschwindigkeit $h‘$ in Abhängigkeit von der Zeit $t$ für die Phase C dargestellt.
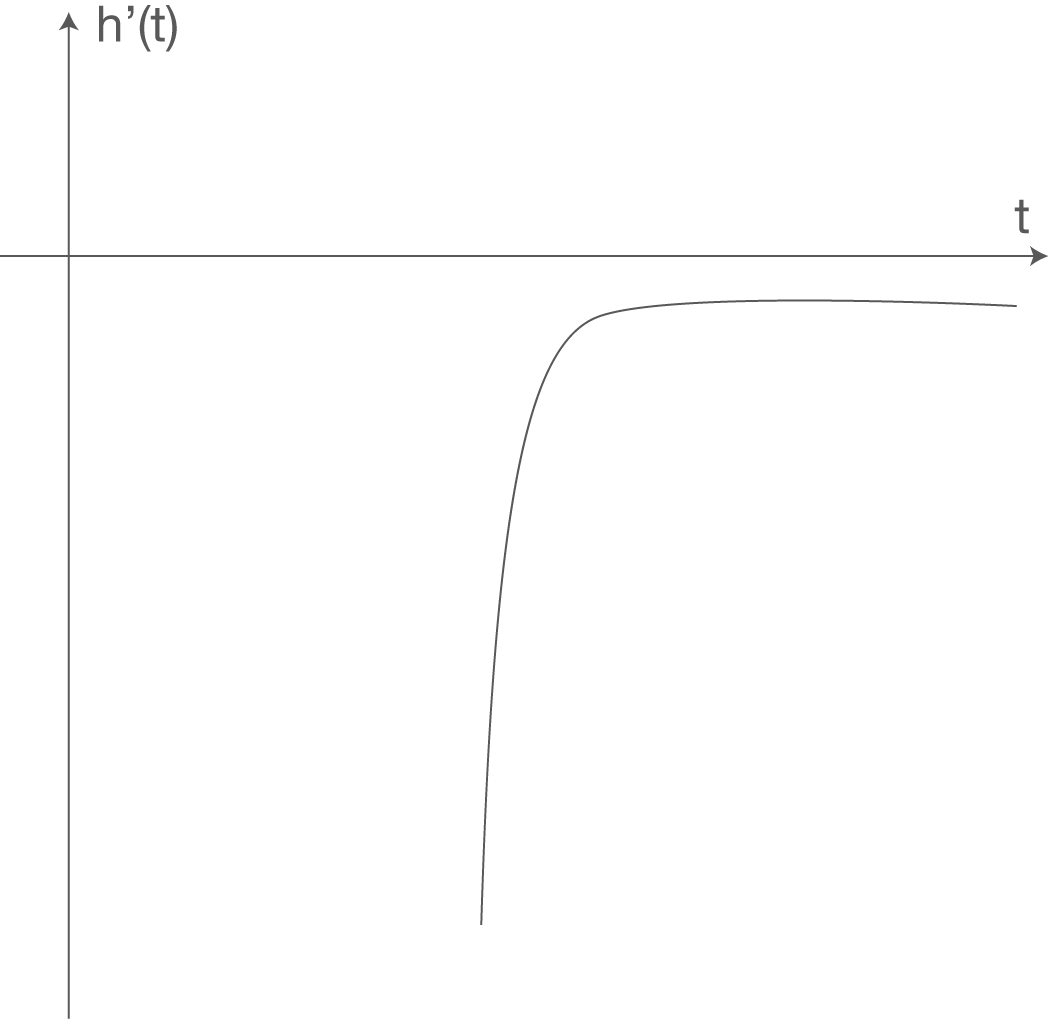
Beschreiben Sie die Bewegung des Fallschirmspringers in Phase C anhand des Graphen der Sinkgeschwindigkeit $h‘$ .
Skizzieren Sie in diesem Koordinatensystem den Graphen der Sinkgeschwindigkeit $h‘$ in Abhängigkeit von der Zeit $t$ für die Phasen A und B.

(9P)

c) Nach 16 Sekunden öffnet der Springer den Fallschirm und leitet damit die Phase C ein.
Die Höhe in dieser Phase soll durch $h_{C}$ mit $h_{C}(t)=\frac{45}{2}\cdot\mathrm{e}^{-2\cdot t+32}-5\cdot t+757,5$ modelliert werden.
Berechnen Sie den Zeitpunkt, zu dem der Springer den Boden erreicht, und dessen Landegeschwindigkeit.
Der Graph von $h_{C}$ schließt stetig und differenzierbar an den Graphen von $h_{B}$ an. Die zweite Ableitung von $h_C$ ist gegeben durch $h_{C}\;‘‘(t)=90\cdot\mathrm{e}^{-2\cdot t+32}$ .
Weisen Sie nach, dass die Modellierungen für die Phasen B und C an der Anschlussstelle bei $t_{2}=16\,\text{s}$ in ihrer zweiten Ableitung nicht übereinstimmen.
Erläutern Sie, wie sich diese fehlende Übereinstimmung im Graphen für die Sinkgeschwindigkeit bemerkbar macht.
Betrachtet wird jetzt noch einmal der Übergang zwischen den Phasen A und B.
Untersuchen Sie, ob es eine quadratische Funktion gibt, die in ihrer zweiten Ableitung mit der zweiten Ableitung von $h_{B}$ übereinstimmt.

(14P)

(34P)

Material

Anlage: Graphen zur Modellierung eines Fallschirmsprungs zu Teilaufgabe b)

Abbildung 1 (nicht maßstabsgetreu)

Graph mit mehreren Funktionen h(t) über der Zeit t, die abnehmende Werte zeigen.

Abbildung 2 (nicht maßstabsgetreu)

Grafische Darstellung von Linien in verschiedenen Höhen auf schwarzem Hintergrund.

a) $\blacktriangleright$ Sinkgeschwindigkeit bestimmen

In Phase B wird der Fallschirmsprung durch die Funktion $h_B$ mit $h_{B}(t)=1.500-50\cdot t$ modelliert.
Du sollst die Sinkgeschwindigkeit des Fallschirmspringers in Phase B bestimmen. Diese kannst du mithilfe der ersten Ableitung bestimmen:

$h_{B}‘(t) = -50$

Die Sinkgeschwindigkeit des Fallschirmspringers in Phase B beträgt also $50 m/s$ .

$\blacktriangleright$ Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen

Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion $h_{A}$ mit $h_A(t)=a\cdot t^{2}+b\cdot t+c$ modelliert werden. Diese soll zum Zeitpunkt $t_{1}=8\,\text{s}$ stetig und differenzierbar an $h_{B}$ anschließen. Das bedeutet, dass die beiden Funktionen für $t_1 = 8$ den gleichen Funktionswert haben, es gilt also $h_{A}(8) = h_{B}(8)$ :

$h_{A}(8) = h_{B}(8)= 1500 - 50 \cdot 8 = 1500 - 400 = 1100$

Der Graph von $h_A$ verläuft also durch den Punkt $(8\mid1.100)$ . Der Übergang soll stetig und differenzierbar sein, das bedeutet, dass die Funktionen die gleiche Steigung für $t_1$ haben müssen, es gilt also $h_{A}‘(8) = h_{B}‘(8)$ :

$h_{A}‘(8) = h_{B}‘(8) = -50$ mit $h_A‘(t) = 2\cdot a\cdot t + b$

Für die Ableitung von $h_A$ gilt also $h_A‘(8)=-50$ . Der Graph soll außerdem durch den Punkt $(4\mid1.250)$ verlaufen.
Du hast nun 3 Bedingungen um den Funktionsterm für $h_A$ bestimmen zu können.

1. Bedingung:

$\begin{array}{rll} 1.100&=&h_A(8)&\\ 1.100&=&a\cdot 8^2 + b\cdot 8 + c&\\ 1.100&=&64\cdot a + 8\cdot b +c& \end{array}$

2. Bedingung:

$\begin{array}{rll} 1.250&=&h_A(4)&\\ 1.250&=&a\cdot 4^2 + b\cdot 4 +c&\\ 1.250&=&16\cdot a + 4\cdot b +c& \end{array}$

3. Bedingung:

$\begin{array}{rll} -50&=&h_A‘(8)& \\ -50&=&16 \cdot a +b&\scriptsize \mid\; -16\cdot a\\ b &=& -50 -16\cdot a& \end{array}$

Subtrahiere nun die zweite von der ersten Bedingung:

$\begin{array}{rll} 1.100 - 1.250&=&64\cdot a + 8\cdot b + c -(16\cdot a + 4\cdot b +c)&\\ - 150&=&64\cdot a + 8\cdot b + c -16\cdot a - 4\cdot b -c&\\ - 150&=&48\cdot a + 4\cdot b & \end{array}$

In diese Gleichung kannst du nun die dritte Bedingung einsetzen:

$\begin{array}{rll} - 150&=&48\cdot a + 4\cdot (-50 -16\cdot a) &\\ - 150&=&48\cdot a -200 -64\cdot a &\\ - 150&=&-16\cdot a -200&\scriptsize \mid\;+200 \\ 50&=&-16\cdot a &\scriptsize \mid\;: (-16)\\ a&=&-\frac{50}{16} = -\frac{25}{8}& \end{array}$

Für den Parameter $a$ gilt also $a = -\frac{25}{8}$ .
Setze dieses Ergebnis jetzt in die 3. Bedingung ein, um den Parameter $b$ zu berechnen.

$b = -50 -16\cdot \left(-\frac{25}{8}\right) = -50 + 50 = 0$

Für den Parameter $b$ gilt also $b = 0$ .
Setze dieses Ergebnis jetzt in die 1. oder 2. Bedingung ein, um den Parameter $c$ zu berechnen.

$\begin{array}{rll} 1.250&=&16\cdot a + 4\cdot b +c &\\ 1.250&=&16\cdot \left(-\frac{25}{8}\right) + 4\cdot 0 +c &\\ 1.250&=&-50 +c &\scriptsize\mid\;+50\\ c &=& 1.300& \end{array}$

Für den Parameter $c$ gilt also $c =1.300$ .
Die Funktionsgleichung für $h_A$ ist gegeben durch $h_A(t) = -\frac{25}{8}\cdot t^2 + 1.300$ .

b) $\blacktriangleright$ Grenzen der Phasen einzeichnen

Du sollst in Abbildung 1 die Grenzen der Phasen A, B und C näherungsweise einzeichnen. Diese Abbildung der Anlage zeigt die Höhe $h$ des Springers in Abhängigkeit von der Zeit $t$ . Du kennst die Funktionen der Phase A und der Phase B. Phase A wird durch eine quadratische Funktion beschrieben und Phase B durch eine Gerade, dementsprechend prüfe den Graphen in Abbildung 1 auf Übergänge von einer quadratischen Funktion in eine Gerade und den Übergang von der Geraden in eine andere Funktion. Du erhältst dann folgende Abbildung:

Diagramm mit mehreren Phasen und Kurvenverläufen über der Zeit.

$\blacktriangleright$ Bewegung des Fallschirmspringers in Phase C

Betrachte hierzu die Abbildung 2. Zu Beginn von Phase C steigt der Graph von $h‘$ schnell, das bedeutet, dass der Fallschirmspringer stark abgebremst wird. Der Betrag der Sinkgeschwindigkeit nimmt stark ab. Dann wird der Graph wesentlich flacher und bleibt nahezu konstant, das bedeutet, dass die Sinkgeschwindigkeit dann nahezu konstant bleibt.
Skizziere jetzt in das Koordinatensystem von Abbildung 2 den Graphen der Sinkgeschwindigkeit $h‘$ in Abhängigkeit von der Zeit $t$ für die Phasen A und B ein. Für Phase A ist die Sinkgeschwindigkeit durch die Ableitung von $h_A$ gegeben, $h_A‘(t) = -\frac{25}{4}t$ . Das ist also eine Gerade, deren Graph durch den Ursprung verläuft und eine negative Steigung besitzt. Für Phase B ist die Sinkgeschwindigkeit konstant $-50$ (vergleiche Aufgabenteil a). Der Graph der Sinkgeschwindigkeit ist dann gegeben durch:

Graphische Darstellung von Funktionen mit verschiedenen Verläufen in einem Koordinatensystem.

c) $\blacktriangleright$ Zeitpunkt der Landung berechnen

Nach 16 Sekunden öffnet der Springer den Fallschirm und leitet damit die Phase C ein.
Die Höhe in dieser Phase wird durch $h_{C}(t)=\frac{45}{2}\cdot\mathrm{e}^{-2\cdot t+32}-5\cdot t+757,5$ modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Graphiktaschenrechner ein und zeichne den Graphen von $h_C$ . Mithilfe der zero-Funktion aus dem CALC-Menü kannst du die Nullstelle berechnen, die dir den Zeitpunkt der Landung angibt.

Diagramm eines mathematischen Graphen auf einem Taschenrechner mit Koordinaten und Funktionsgleichung.

Die Nullstelle ist gegeben durch $t_{NS} = 151,5$ , somit ist der Zeitpunkt der Landung nach $151,5$ Sekunden.

$\blacktriangleright$ Landegeschwindigkeit berechnen

Außerdem sollst du dessen Landegeschwindigkeit berechnen. Da du jetzt den Zeitpunkt der Landung kennst, kannst du erneut deinen Graphiktaschenrechner zur Hand nehmen und die $dy/dx$ -Funktion aus dem CALC-Menü verwenden, um die Steigung im Landepunkt zu berechnen.

Grafische Darstellung einer mathematischen Funktion mit Ableitung und Koordinaten.

Alternativ
Du kannst auch von Hand die Ableitung von $h_C$ bestimmen und so die Steigung für $t = 151,5$ berechnen.

$h_c‘(t) = -45\cdot \mathrm e^{-2t + 32} -5$

$h_c‘(151,5) = -45\cdot \mathrm e^{-170} -5 \approx -5$

Die Landegeschwindigkeit beträgt $5 m/s$ .

$\blacktriangleright$ Übereinstimmen der 2. Ableitungen

Der Graph von $h_{C}$ schließt stetig und differenzierbar an den Graphen von $h_{B}$ an. Die zweite Ableitung von $h_C$ ist gegeben durch $h_{C}\;‘‘(t)=90\cdot\mathrm{e}^{-2\cdot t+32}$ .
Du sollst nun nachweisen, dass die Modellierungen für die Phasen B und C an der Anschlussstelle bei $t_{2}=16\,\text{s}$ in ihrer zweiten Ableitung nicht übereinstimmen. Berechne dafür die 2. Ableitung von $h_B$ :

$h_B‘ (t) = -50$ $\quad$ $h_B‘‘ (t) = 0$

Setze jetzt in beide Ableitungen $t_2 = 16$ ein:

$\begin{array}{rll} h_B‘‘ (16)&=&0&\\ h_C‘‘ (16)&=&90& \end{array}$

Die zweiten Ableitungen von $h_B$ und $h_C$ stimmen nicht überein, die fehlende Übereinstimmung hat einen Knick im Graphen der Sinkgeschwindigkeit zur Folge.

$\blacktriangleright$ Übergang zwischen Phasen A und B

Du sollst untersuchen, ob es eine quadratische Funktion gibt, die in ihrer zweiten Ableitung mit der zweiten Ableitung von $h_{B}$ übereinstimmt. Leite dafür die allgemeine Form von $h_A$ aus Aufgabenteil a) zweimal ab:

$\begin{array}{rll} h_A(t)&=&a\cdot t^2 + b\cdot t +c&\\ h_A‘(t)&=&2\cdot a\cdot t + b&\\ h_A‘‘(t)&=&2\cdot a& \end{array}$

Die zweite Ableitung von $h_B$ ist gegeben durch $h_B‘‘(t) = 0$ . Setze nun $h_B‘‘(t) = h_A‘‘(t)$ :

$\begin{array}{rll} h_B‘‘(t)&=&h_A‘‘(t)&\\ 0&=&2\cdot a&\scriptsize \scriptsize\mid\; : 2\\ 0&=&a& \end{array}$

Für $a=0$ stimmen die zweiten Ableitung überein, doch dann ist $h_A$ keine quadratische Funktion mehr (der Teil mit $x^2$ wird eliminiert). Somit existiert keine solche quadratische Funktion.

a) $\blacktriangleright$ Sinkgeschwindigkeit bestimmen

$h_{B}‘(t) = -50$

Die Sinkgeschwindigkeit des Fallschirmspringers in Phase B beträgt also $50 m/s$ .

$\blacktriangleright$ Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen

$h_{A}(8) = h_{B}(8)= 1500 - 50 \cdot 8 = 1500 - 400 = 1100$

$h_{A}‘(8) = h_{B}‘(8) = -50$ mit $h_A‘(t) = 2\cdot a\cdot t + b$

1. Bedingung:

$\begin{array}{rll} 1.100&=&h_A(8)&\\ 1.100&=&a\cdot 8^2 + b\cdot 8 + c&\\ 1.100&=&64\cdot a + 8\cdot b +c& \end{array}$

2. Bedingung:

$\begin{array}{rll} 1.250&=&h_A(4)&\\ 1.250&=&a\cdot 4^2 + b\cdot 4 +c&\\ 1.250&=&16\cdot a + 4\cdot b +c& \end{array}$

3. Bedingung:

$\begin{array}{rll} -50&=&h_A‘(8)& \\ -50&=&16 \cdot a +b&\scriptsize \mid\; -16\cdot a\\ b &=& -50 -16\cdot a& \end{array}$

Subtrahiere nun die zweite von der ersten Bedingung:

$\begin{array}{rll} 1.100 - 1.250&=&64\cdot a + 8\cdot b + c -(16\cdot a + 4\cdot b +c)&\\ - 150&=&64\cdot a + 8\cdot b + c -16\cdot a - 4\cdot b -c&\\ - 150&=&48\cdot a + 4\cdot b & \end{array}$

In diese Gleichung kannst du nun die dritte Bedingung einsetzen:

Für den Parameter $a$ gilt also $a = -\frac{25}{8}$ .
Setze dieses Ergebnis jetzt in die 3. Bedingung ein, um den Parameter $b$ zu berechnen.

$b = -50 -16\cdot \left(-\frac{25}{8}\right) = -50 + 50 = 0$

Für den Parameter $b$ gilt also $b = 0$ .
Setze dieses Ergebnis jetzt in die 1. oder 2. Bedingung ein, um den Parameter $c$ zu berechnen.

$\begin{array}{rll} 1.250&=&16\cdot a + 4\cdot b +c &\\ 1.250&=&16\cdot \left(-\frac{25}{8}\right) + 4\cdot 0 +c &\\ 1.250&=&-50 +c &\scriptsize\mid\;+50\\ c &=& 1.300& \end{array}$

Für den Parameter $c$ gilt also $c =1.300$ .
Die Funktionsgleichung für $h_A$ ist gegeben durch $h_A(t) = -\frac{25}{8}\cdot t^2 + 1.300$ .

b) $\blacktriangleright$ Grenzen der Phasen einzeichnen

$\blacktriangleright$ Bewegung des Fallschirmspringers in Phase C

c) $\blacktriangleright$ Zeitpunkt der Landung berechnen

Nach 16 Sekunden öffnet der Springer den Fallschirm und leitet damit die Phase C ein.
Die Höhe in dieser Phase wird durch $h_{C}(t)=\frac{45}{2}\cdot\mathrm{e}^{-2\cdot t+32}-5\cdot t+757,5$ modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Graphiktaschenrechner ein und zeichne den Graphen von $h_C$ . Mithilfe der Root-Funktion aus dem G-Solv-Menü-Menü kannst du die Nullstelle berechnen, die dir den Zeitpunkt der Landung angibt.

Grafische Darstellung einer mathematischen Funktion mit einer Wurzel bei x = 151,5 und y = 0.

Die Nullstelle ist gegeben durch $t_{NS} = 151,5$ , somit ist der Zeitpunkt der Landung nach $151,5$ Sekunden.

$\blacktriangleright$ Landegeschwindigkeit berechnen

Außerdem sollst du dessen Landegeschwindigkeit berechnen. Da du jetzt den Zeitpunkt der Landung kennst, kannst du erneut deinen Graphiktaschenrechner zur Hand nehmen und im Graph-Menü

optn CALC d/dx

die erste Ableitungsfunkion von $h$ bilden. Lässt du dir den zugehörigen Graphen anzeigen, so kannst du unter

G-Solv F6 Y-CAL

$x = 151, 5$ eingeben und mit EXE bestätigen. Du erhältst dann das Ergebnis: $h′_{c}(151, 5) = −5$

Diagramm mit mathematischen Funktionen und Werten für X und Y.

Alternativ
Du kannst auch von Hand die Ableitung von $h_C$ bestimmen und so die Steigung für $t = 151,5$ berechnen.

$h_c‘(t) = -45\cdot \mathrm e^{-2t + 32} -5$

$h_c‘(151,5) = -45\cdot \mathrm e^{-170} -5 \approx -5$

Die Landegeschwindigkeit beträgt $5 m/s$ .

$\blacktriangleright$ Übereinstimmen der 2. Ableitungen

$h_B‘ (t) = -50$ $\quad$ $h_B‘‘ (t) = 0$

Setze jetzt in beide Ableitungen $t_2 = 16$ ein:

$\begin{array}{rll} h_B‘‘ (16)&=&0&\\ h_C‘‘ (16)&=&90& \end{array}$

Die zweiten Ableitungen von $h_B$ und $h_C$ stimmen nicht überein, die fehlende Übereinstimmung hat einen Knick im Graphen der Sinkgeschwindigkeit zur Folge.

$\blacktriangleright$ Übergang zwischen Phasen A und B

$\begin{array}{rll} h_A(t)&=&a\cdot t^2 + b\cdot t +c&\\ h_A‘(t)&=&2\cdot a\cdot t + b&\\ h_A‘‘(t)&=&2\cdot a& \end{array}$

Die zweite Ableitung von $h_B$ ist gegeben durch $h_B‘‘(t) = 0$ . Setze nun $h_B‘‘(t) = h_A‘‘(t)$ :

$\begin{array}{rll} h_B‘‘(t)&=&h_A‘‘(t)&\\ 0&=&2\cdot a&\scriptsize \scriptsize\mid\; : 2\\ 0&=&a& \end{array}$

Für $a=0$ stimmen die zweiten Ableitung überein, doch dann ist $h_A$ keine quadratische Funktion mehr (der Teil mit $x^2$ wird eliminiert). Somit existiert keine solche quadratische Funktion.