Aufgabe 3A
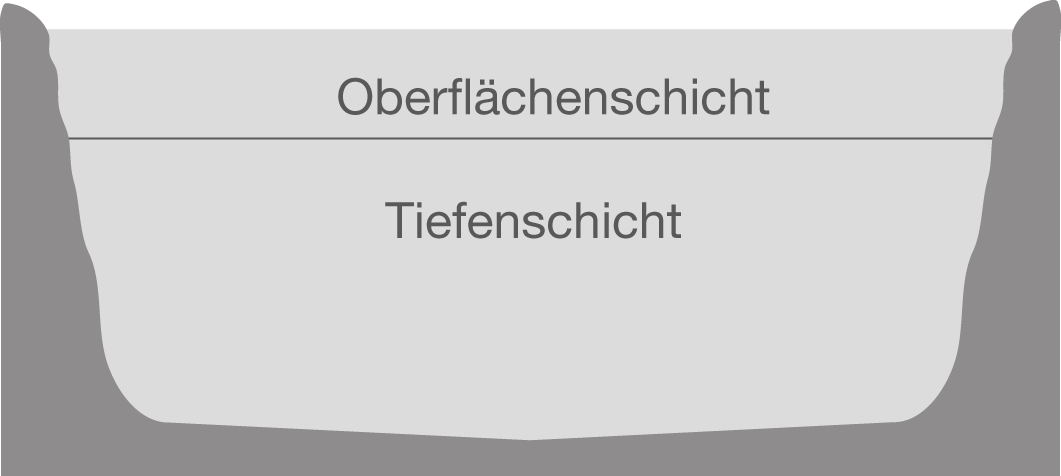
Stehende Gewässer weisen eine Schichtung des Wassers auf. Modellhaft werden zwei Schichten unterschieden: die kalte Tiefenschicht und die warme Oberflächenschicht.
Durch unterschiedliche Vorgänge kommt es zu einem gewissen Austausch zwischen den Schichten, sodass sich die Schichtdicken verändern.
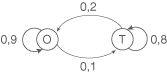 Für ein Gewässer beschreibt der nebenstehende Übergangsgraph die Übergänge zwischen den Schichten pro Zeiteinheit. Für diese Modellierung wird vorausgesetzt, dass sich diese Entwicklung in der beschriebenen Weise fortsetzen wird.
Für ein Gewässer beschreibt der nebenstehende Übergangsgraph die Übergänge zwischen den Schichten pro Zeiteinheit. Für diese Modellierung wird vorausgesetzt, dass sich diese Entwicklung in der beschriebenen Weise fortsetzen wird.

a) Stellen Sie den Austauschvorgang in einer Übergangsmatrix  dar.
dar.
Erläutern Sie die Werte der ersten Zeile von im Sachzusammenhang.
im Sachzusammenhang.
Bestimmen Sie die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau, wenn zu Beginn beide Schichten 6 m dick sind.
Erläutern Sie die Werte der ersten Zeile von
Bestimmen Sie die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau, wenn zu Beginn beide Schichten 6 m dick sind.
(8P)
b) Im Laufe des Sommers stabilisiert sich die Schichtenverteilung.
Bestimmen Sie die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung.
Bestimmen Sie die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung.
(4P)
c) In einem anderen Gewässer liegt ein anderes Übergangsverhalten vor. Zu Beginn sind beide Schichten unterschiedlich dick.
Erstellen Sie begründet ein Beispiel für eine Übergangsmatrix so, dass beide Schichten auf lange Sicht gleich dick werden.
Erstellen Sie begründet ein Beispiel für eine Übergangsmatrix so, dass beide Schichten auf lange Sicht gleich dick werden.
(5P)
(17P)
a)  Übergangsmatrix bestimmen
Du sollst den Austauschvorgang in einer Übergangsmatrix
Übergangsmatrix bestimmen
Du sollst den Austauschvorgang in einer Übergangsmatrix  darstellen. Auf der Diagonalen stehen die Anteile, die in der jeweiligen Schicht erhalten bleiben, die anderen Einträge geben die Anteile an, die in die jeweils andere Schicht übergehen. Trägst du die Oberflächenschicht in der ersten Zeile und Spalte ein und dementsprechend die Tiefenschicht in der zweiten Zeile und Spalte, so ergibt sich folgende Übergangsmatrix
darstellen. Auf der Diagonalen stehen die Anteile, die in der jeweiligen Schicht erhalten bleiben, die anderen Einträge geben die Anteile an, die in die jeweils andere Schicht übergehen. Trägst du die Oberflächenschicht in der ersten Zeile und Spalte ein und dementsprechend die Tiefenschicht in der zweiten Zeile und Spalte, so ergibt sich folgende Übergangsmatrix  :
:

 Werte der ersten Zeile von
Werte der ersten Zeile von  Erläutere nun die Werte der ersten Zeile von
Erläutere nun die Werte der ersten Zeile von  im Sachzusammenhang. Der Eintrag
im Sachzusammenhang. Der Eintrag  der ersten Zeile gibt an, welcher Anteil in der Oberflächenschicht erhalten bleibt. Der Eintrag
der ersten Zeile gibt an, welcher Anteil in der Oberflächenschicht erhalten bleibt. Der Eintrag  der ersten Zeile gibt an, welcher Anteil von der Tiefenschicht zur Oberflächenschicht hinzu kommt.
der ersten Zeile gibt an, welcher Anteil von der Tiefenschicht zur Oberflächenschicht hinzu kommt.
 Verteilung der Schichten nach fünf Zeiteinheiten
Du sollst die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau bestimmen, wenn zu Beginn beide Schichten 6 m dick sind.
Verteilung der Schichten nach fünf Zeiteinheiten
Du sollst die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau bestimmen, wenn zu Beginn beide Schichten 6 m dick sind.
Die Übergangsmatrix gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Jetzt musst du noch die Schichtdicke von je 6 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:
gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Jetzt musst du noch die Schichtdicke von je 6 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:
 Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht
Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht  und die der Tiefenschicht beträgt
und die der Tiefenschicht beträgt  .
.
Die Übergangsmatrix
b)  Dicke der einzelnen Schichten bestimmen
Im Laufe des Sommers stabilisiert sich die Schichtenverteilung. Bestimme die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung. Dies ist eine Verteilung
Dicke der einzelnen Schichten bestimmen
Im Laufe des Sommers stabilisiert sich die Schichtenverteilung. Bestimme die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung. Dies ist eine Verteilung  , sodass folgende Gleichung gilt:
, sodass folgende Gleichung gilt:
 Dafür definiere:
Dafür definiere:
 : Dicke der Oberflächenschicht
: Dicke der Oberflächenschicht
 : Dicke der Tiefenschicht
Du erhältst folgendes Gleichungssystem für die Schichtdicken:
: Dicke der Tiefenschicht
Du erhältst folgendes Gleichungssystem für die Schichtdicken:

 Außerdem kannst du der Aufgabenstellung
Außerdem kannst du der Aufgabenstellung  entnehmen. Löse diese Gleichung nach
entnehmen. Löse diese Gleichung nach  auf und setze das Ergebnis in eine der beiden Zeilen des Gleichungssystems ein, um
auf und setze das Ergebnis in eine der beiden Zeilen des Gleichungssystems ein, um  zu bestimmen:
zu bestimmen:
 Einsetzen in (2) ergibt:
Einsetzen in (2) ergibt:
 Für
Für  ergibt sich dann
ergibt sich dann  . scriptsize Die Oberflächenschicht ist somit
. scriptsize Die Oberflächenschicht ist somit  dick, die Tiefenschicht ist
dick, die Tiefenschicht ist  dick.
dick.
c)  Übergangsmatrix bestimmen
In einem anderen Gewässer liegt ein anderes Übergangsverhalten vor. Zu Beginn sind beide Schichten unterschiedlich dick, doch auf lange Sicht sollen beide Schichten gleich dick werden. Das bedeutet, dass die Anteile, die ausgetauscht werden, gleich groß sein sollten. Also der Übergangsanteil von Oberflächenschicht in die Tiefenschicht entspricht dem Übergangsanteil von Tiefenschicht in die Oberflächenschicht. Die Übergangsmatrix ist somit symmetrisch zur Hauptdiagonalen und die Einträge auf der Hauptdiagonalen sind die gleichen. Es gibt viele Übergangsmatrizen, die das Übergangsverhalten beschreiben. Ein mögliches Beispiel ist gegeben durch:
Übergangsmatrix bestimmen
In einem anderen Gewässer liegt ein anderes Übergangsverhalten vor. Zu Beginn sind beide Schichten unterschiedlich dick, doch auf lange Sicht sollen beide Schichten gleich dick werden. Das bedeutet, dass die Anteile, die ausgetauscht werden, gleich groß sein sollten. Also der Übergangsanteil von Oberflächenschicht in die Tiefenschicht entspricht dem Übergangsanteil von Tiefenschicht in die Oberflächenschicht. Die Übergangsmatrix ist somit symmetrisch zur Hauptdiagonalen und die Einträge auf der Hauptdiagonalen sind die gleichen. Es gibt viele Übergangsmatrizen, die das Übergangsverhalten beschreiben. Ein mögliches Beispiel ist gegeben durch:
 Mit
Mit  ergibt sich die entsprechende Verteilung.
ergibt sich die entsprechende Verteilung.
a)  Übergangsmatrix bestimmen
Du sollst den Austauschvorgang in einer Übergangsmatrix
Übergangsmatrix bestimmen
Du sollst den Austauschvorgang in einer Übergangsmatrix  darstellen. Auf der Diagonalen stehen die Anteile, die in der jeweiligen Schicht erhalten bleiben, die anderen Einträge geben die Anteile an, die in die jeweils andere Schicht übergehen. Trägst du die Oberflächenschicht in der ersten Zeile und Spalte ein und dementsprechend die Tiefenschicht in der zweiten Zeile und Spalte, so ergibt sich folgende Übergangsmatrix
darstellen. Auf der Diagonalen stehen die Anteile, die in der jeweiligen Schicht erhalten bleiben, die anderen Einträge geben die Anteile an, die in die jeweils andere Schicht übergehen. Trägst du die Oberflächenschicht in der ersten Zeile und Spalte ein und dementsprechend die Tiefenschicht in der zweiten Zeile und Spalte, so ergibt sich folgende Übergangsmatrix  :
:

 Werte der ersten Zeile von
Werte der ersten Zeile von  Erläutere nun die Werte der ersten Zeile von
Erläutere nun die Werte der ersten Zeile von  im Sachzusammenhang. Der Eintrag
im Sachzusammenhang. Der Eintrag  der ersten Zeile gibt an, welcher Anteil in der Oberflächenschicht erhalten bleibt. Der Eintrag
der ersten Zeile gibt an, welcher Anteil in der Oberflächenschicht erhalten bleibt. Der Eintrag  der ersten Zeile gibt an, welcher Anteil von der Tiefenschicht zur Oberflächenschicht hinzu kommt.
der ersten Zeile gibt an, welcher Anteil von der Tiefenschicht zur Oberflächenschicht hinzu kommt.
 Verteilung der Schichten nach fünf Zeiteinheiten
Du sollst die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau bestimmen, wenn zu Beginn beide Schichten 6 m dick sind.
Verteilung der Schichten nach fünf Zeiteinheiten
Du sollst die Verteilung der Schichten nach fünf Zeiteinheiten auf Zentimeter genau bestimmen, wenn zu Beginn beide Schichten 6 m dick sind.
Die Übergangsmatrix gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Dies kannst du mit deinem GTR tun. Eine Matrix kannst du im CALC-Menü unter
gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Dies kannst du mit deinem GTR tun. Eine Matrix kannst du im CALC-Menü unter
Jetzt musst du noch die Schichtdicke von je 6 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:
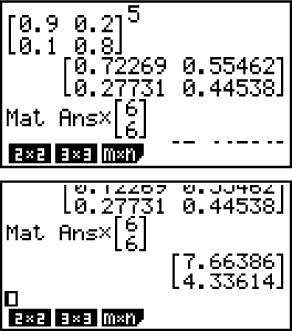 Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht
Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht  und die der Tiefenschicht beträgt
und die der Tiefenschicht beträgt  .
.
Die Übergangsmatrix
F4: MATH  F1: MAT
F1: MAT
eingeben, indemdu zunächst die entsprechende Dimension auswählst. Anschließend kannst du die Matrix potenzieren.
Jetzt musst du noch die Schichtdicke von je 6 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:

b)  Dicke der einzelnen Schichten bestimmen
Im Laufe des Sommers stabilisiert sich die Schichtenverteilung. Bestimme die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung. Dies ist eine Verteilung
Dicke der einzelnen Schichten bestimmen
Im Laufe des Sommers stabilisiert sich die Schichtenverteilung. Bestimme die Dicke der einzelnen Schichten eines 12 m tiefen Gewässers in der stationären Verteilung. Dies ist eine Verteilung  , sodass folgende Gleichung gilt:
, sodass folgende Gleichung gilt:
 Dafür definiere:
Dafür definiere:
 : Dicke der Oberflächenschicht
: Dicke der Oberflächenschicht
 : Dicke der Tiefenschicht
Du erhältst folgendes Gleichungssystem für die Schichtdicken:
: Dicke der Tiefenschicht
Du erhältst folgendes Gleichungssystem für die Schichtdicken:

 Außerdem kannst du der Aufgabenstellung
Außerdem kannst du der Aufgabenstellung  entnehmen. Löse diese Gleichung nach
entnehmen. Löse diese Gleichung nach  auf und setze das Ergebnis in eine der beiden Zeilen des Gleichungssystems ein, um
auf und setze das Ergebnis in eine der beiden Zeilen des Gleichungssystems ein, um  zu bestimmen:
zu bestimmen:
 Einsetzen in (2) ergibt:
Einsetzen in (2) ergibt:
 Für
Für  ergibt sich dann
ergibt sich dann  . scriptsize Die Oberflächenschicht ist somit
. scriptsize Die Oberflächenschicht ist somit  dick, die Tiefenschicht ist
dick, die Tiefenschicht ist  dick.
dick.
c)  Übergangsmatrix bestimmen
In einem anderen Gewässer liegt ein anderes Übergangsverhalten vor. Zu Beginn sind beide Schichten unterschiedlich dick, doch auf lange Sicht sollen beide Schichten gleich dick werden. Das bedeutet, dass die Anteile, die ausgetauscht werden, gleich groß sein sollten. Also der Übergangsanteil von Oberflächenschicht in die Tiefenschicht entspricht dem Übergangsanteil von Tiefenschicht in die Oberflächenschicht. Die Übergangsmatrix ist somit symmetrisch zur Hauptdiagonalen und die Einträge auf der Hauptdiagonalen sind die gleichen. Es gibt viele Übergangsmatrizen, die das Übergangsverhalten beschreiben. Ein mögliches Beispiel ist gegeben durch:
Übergangsmatrix bestimmen
In einem anderen Gewässer liegt ein anderes Übergangsverhalten vor. Zu Beginn sind beide Schichten unterschiedlich dick, doch auf lange Sicht sollen beide Schichten gleich dick werden. Das bedeutet, dass die Anteile, die ausgetauscht werden, gleich groß sein sollten. Also der Übergangsanteil von Oberflächenschicht in die Tiefenschicht entspricht dem Übergangsanteil von Tiefenschicht in die Oberflächenschicht. Die Übergangsmatrix ist somit symmetrisch zur Hauptdiagonalen und die Einträge auf der Hauptdiagonalen sind die gleichen. Es gibt viele Übergangsmatrizen, die das Übergangsverhalten beschreiben. Ein mögliches Beispiel ist gegeben durch:
 Mit
Mit  ergibt sich die entsprechende Verteilung.
ergibt sich die entsprechende Verteilung.