Ähnlichkeit von Figuren
Ähnlichkeit von Figuren
Zwei FigurenWinkel und Längenverhältnisse
Zwei Vielecke- Winkel, die einander entsprechen, gleich groß sind und
- die Längenverhältnisse von Seiten, die einander entsprechen, übereinstimmen.
Ähnlichkeit von Vielecken
Sind zwei Vielecke
1
Entscheide, ob die jeweiligen beiden Figuren ähnlich zueinander sind und begründe deine Entscheidung.
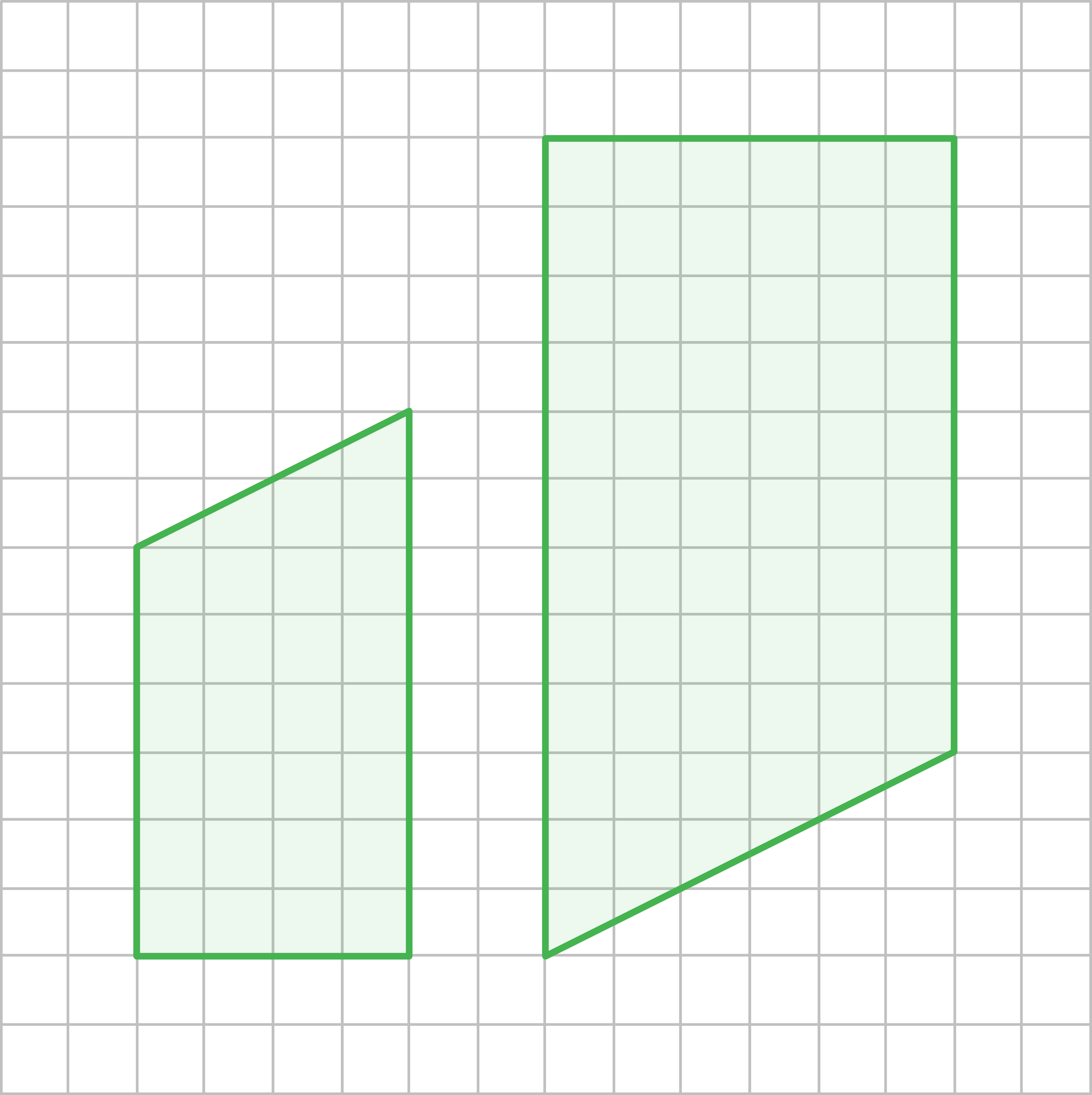
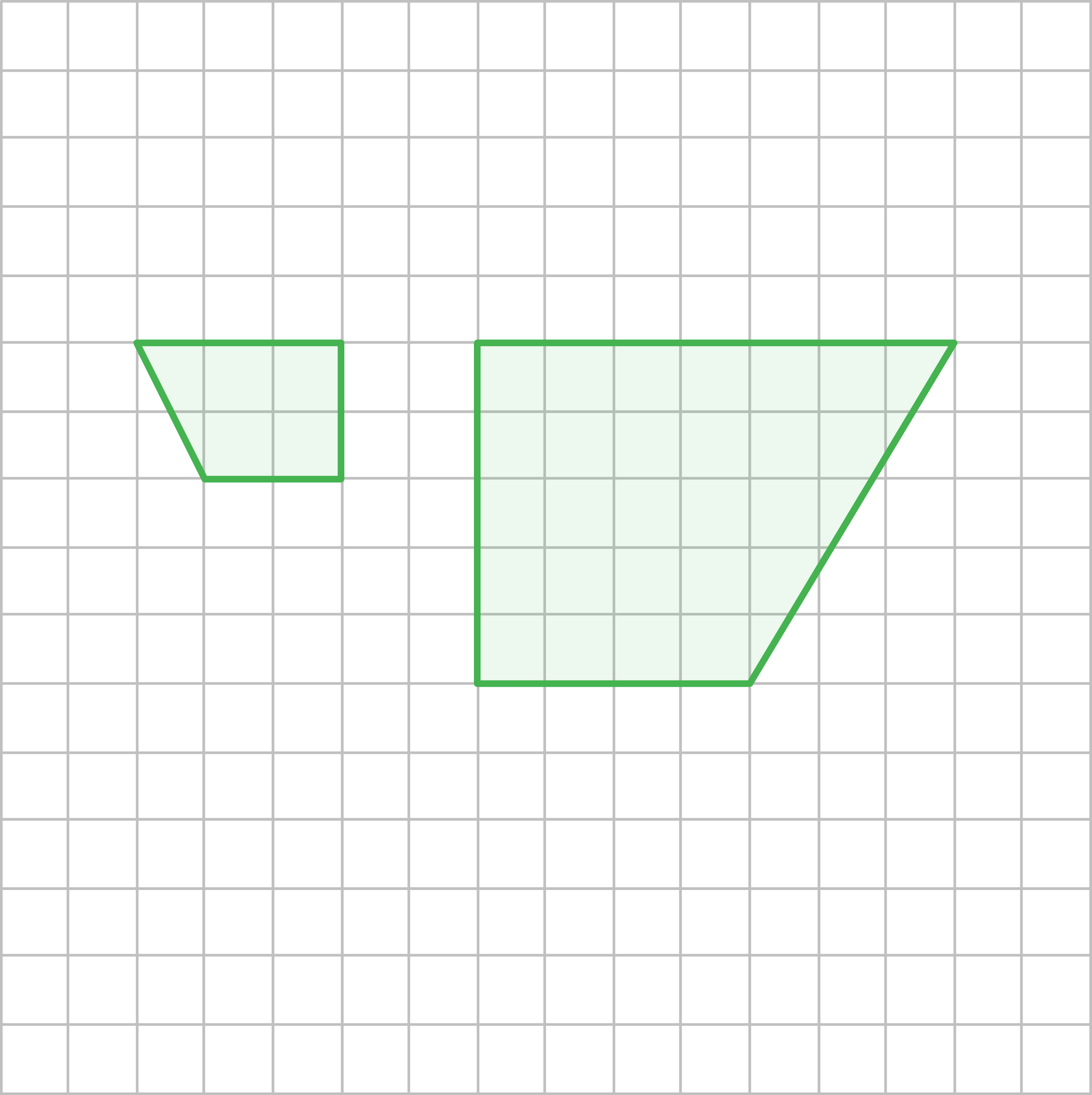
a)

b)

2
Die Dreiecke  und
und  sind zueinander ähnlich.
sind zueinander ähnlich.
Berechne die fehlenden Seitenlängen dieser Dreiecke.
















Berechne die fehlenden Seitenlängen dieser Dreiecke.
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
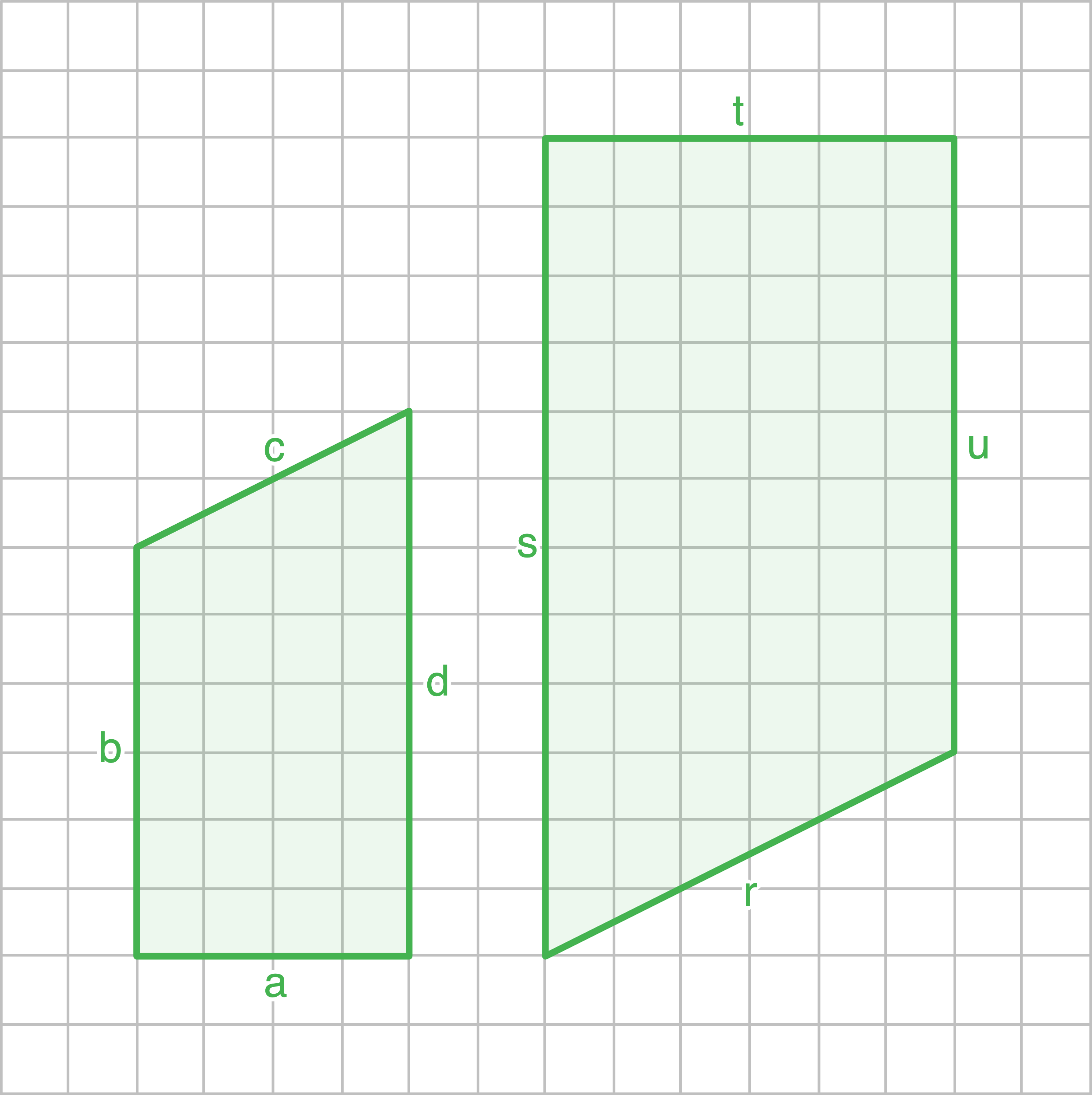
b)
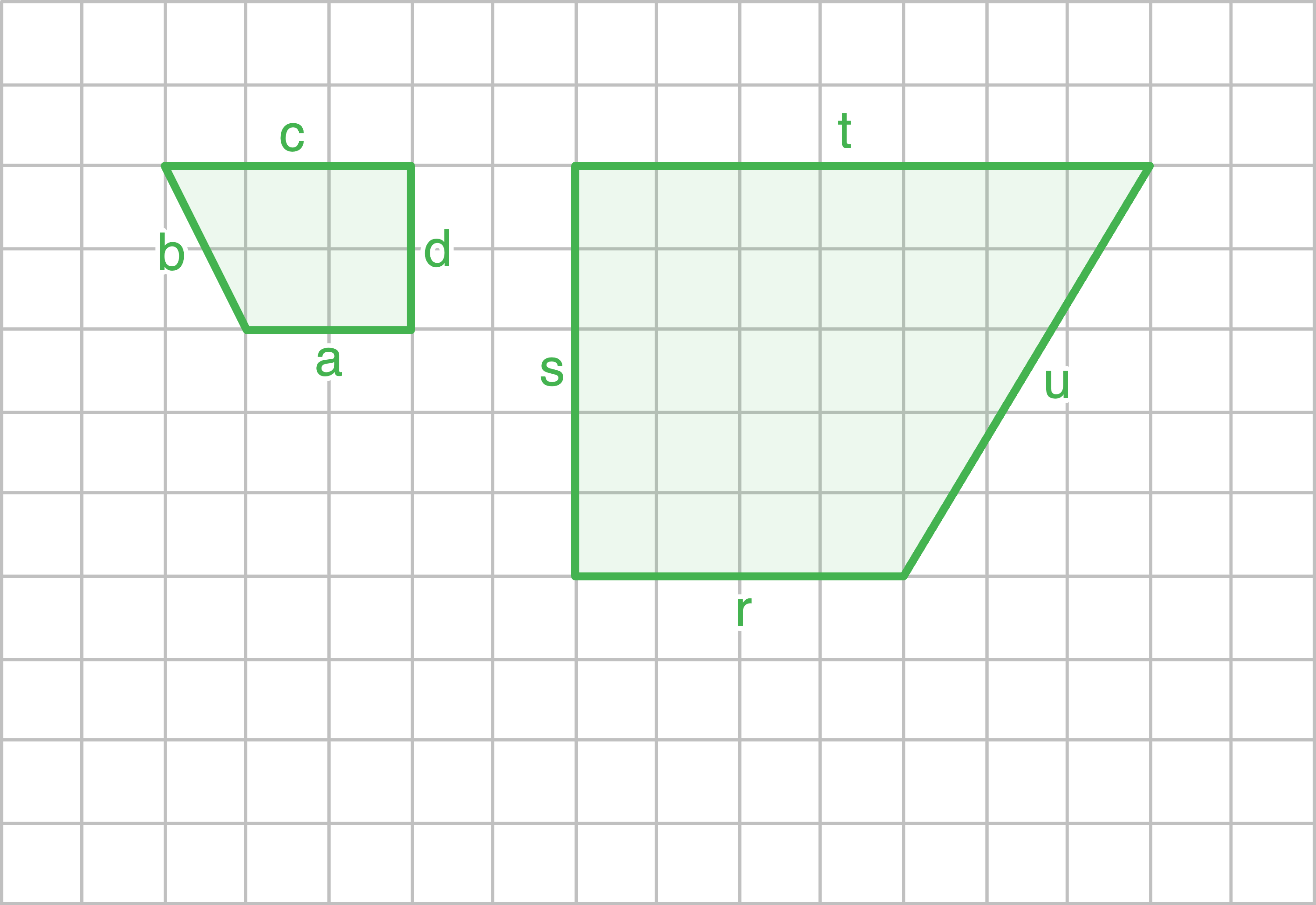
2
a)
b)
c)
d)