Quadratische Funktionen der Form y=(x+d)²
Der Graph der quadratischen Funktion der Form  mit dem Definitionsbereich
mit dem Definitionsbereich  ist eine in
ist eine in  -Richtung verschobene Normalparabel.
Diese wurde um
-Richtung verschobene Normalparabel.
Diese wurde um  Einheiten in
Einheiten in  -Richtung verschoben:
-Richtung verschoben:
- nach rechts für
- nach links für
- Die Symmetrieachse verläuft durch den Scheitelpunkt
und ist eine Parallele zur
-Achse
- Der Scheitelpunkt hat die Koordinaten
- Die Parabel fällt bis zum Scheitelpunkt monoton, danach steigt sie monoton
- Der Wertebereich umfasst die Menge aller reellen Zahlen
ist die einzige Nullstelle
1
Gib den Scheitelpunkt an und zeichne den Graphen der Parabel.




a)
b)
c)
d)
2
Um wie viele Einheiten wurde die ursprüngliche Normalparabel nach rechts bzw. nach links verschoben, damit die verschobene Parabel mit der entsprechenden Funktionsgleichung entsteht?




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
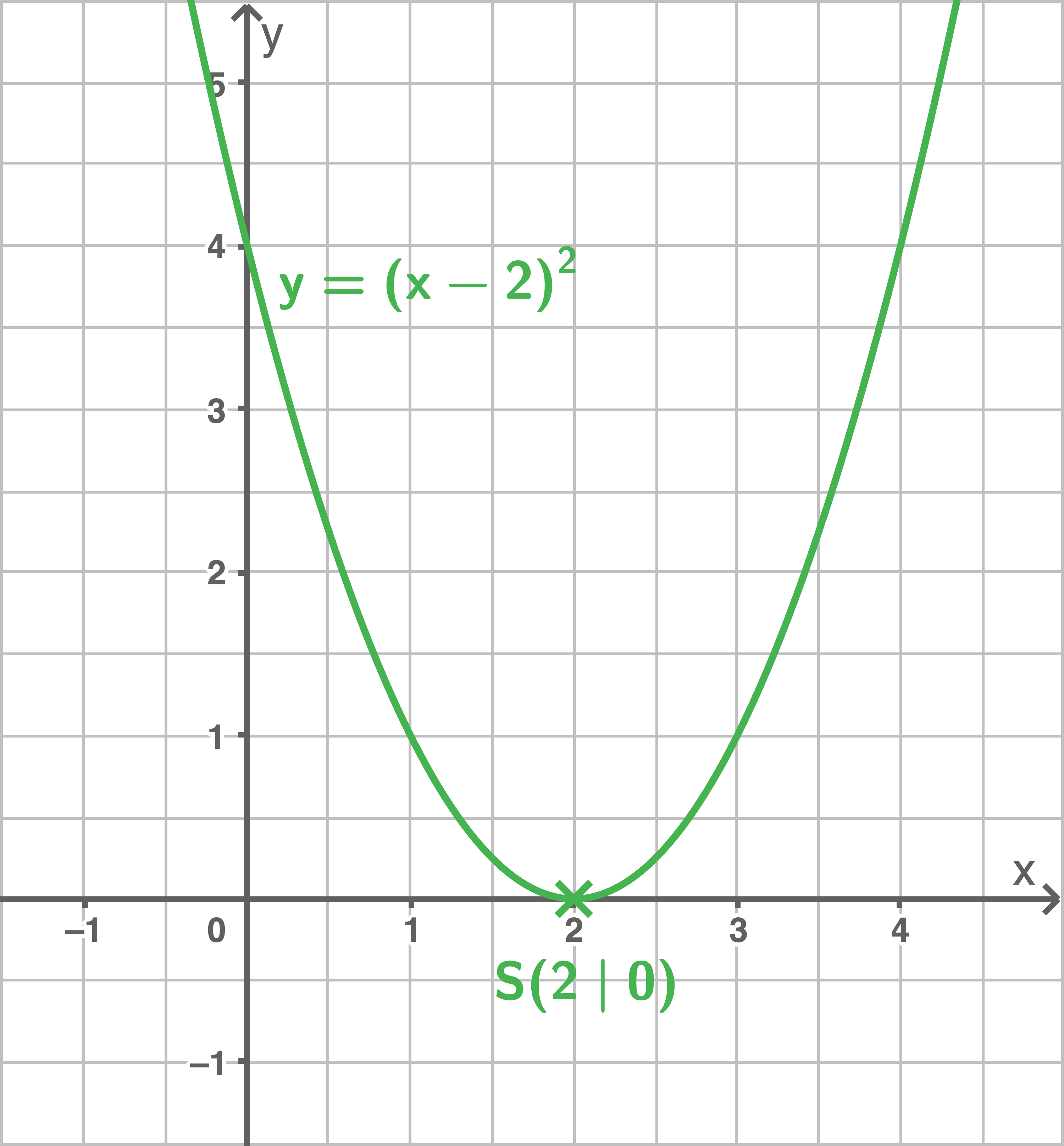
b)
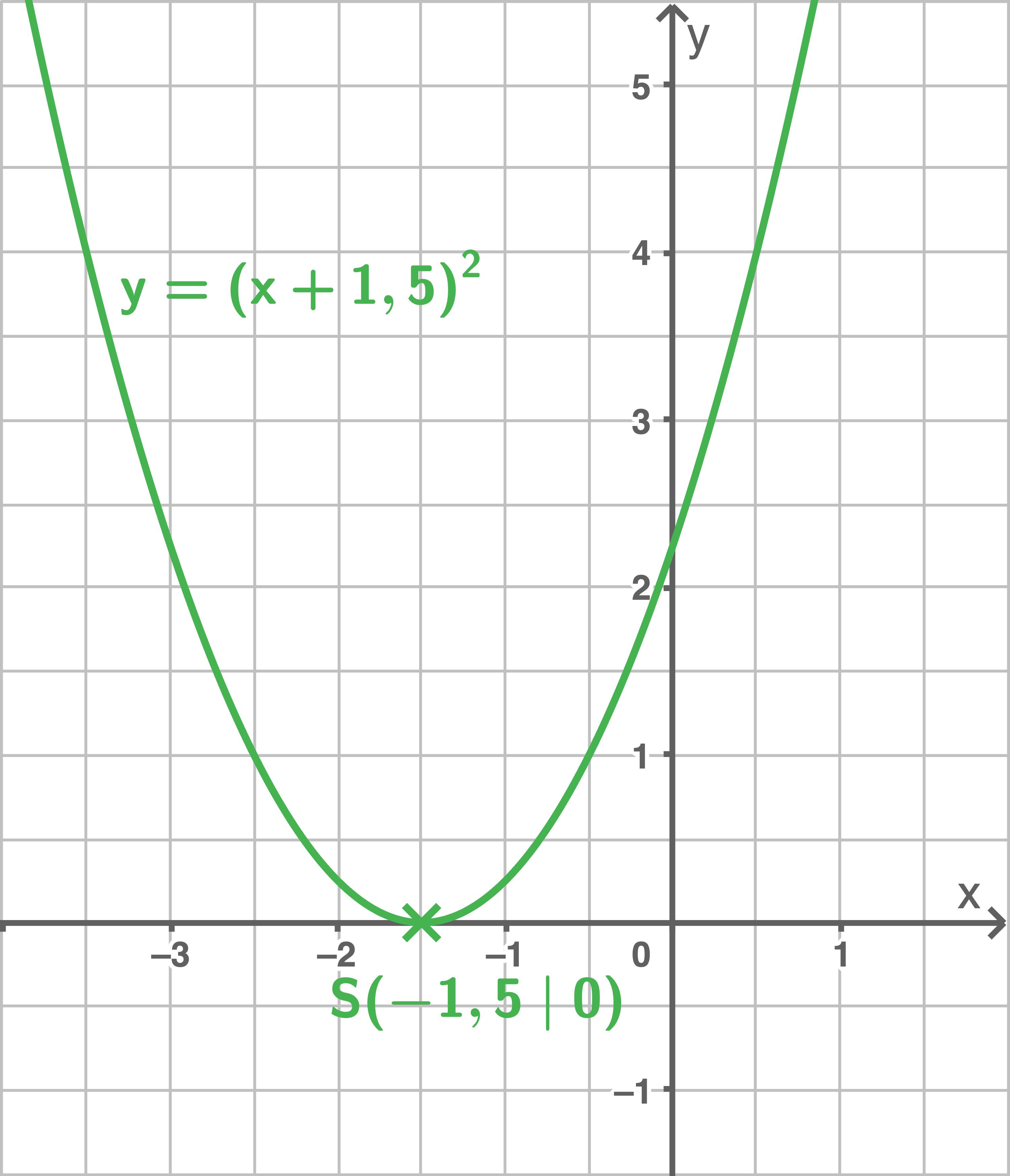
c)
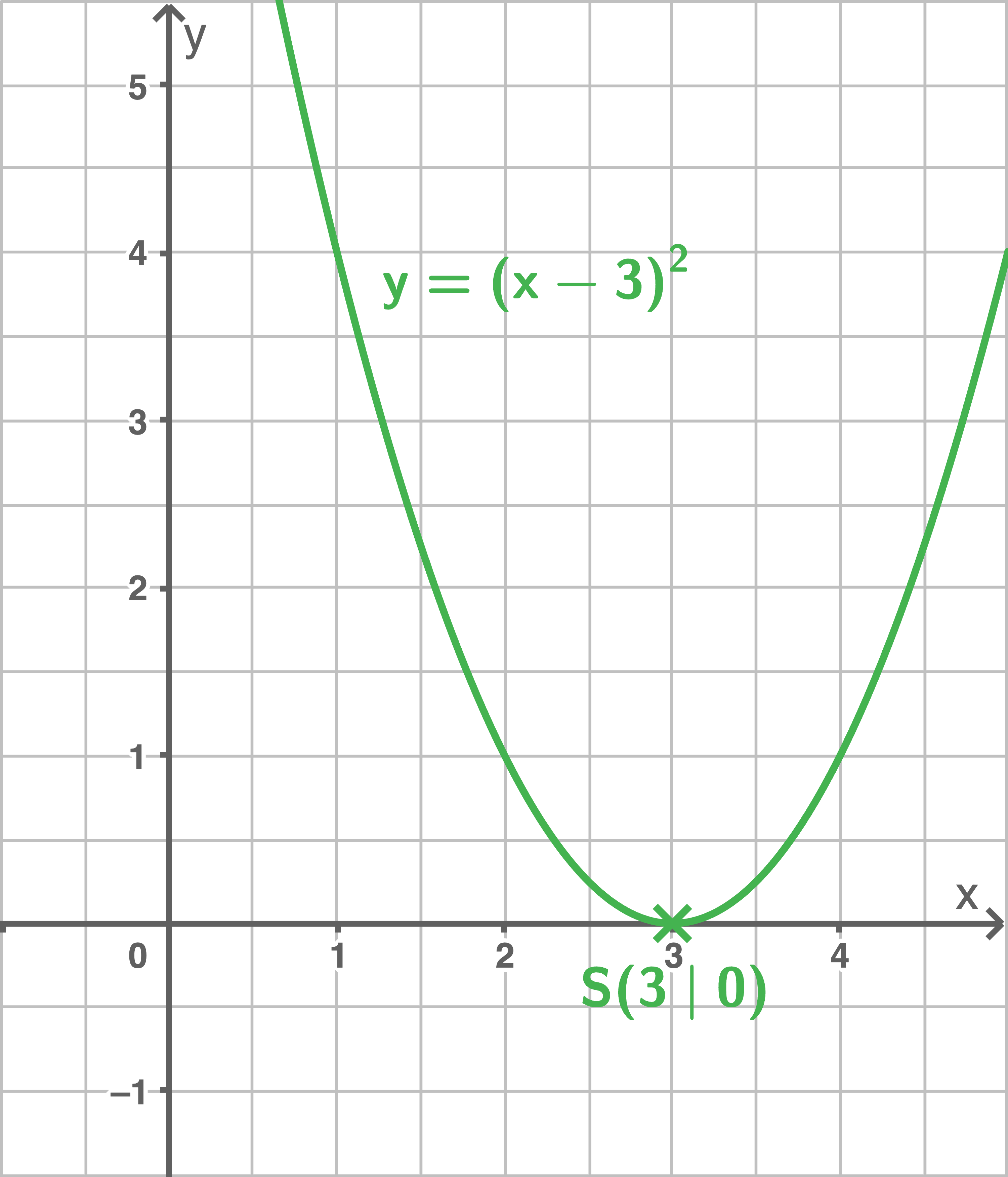
d)
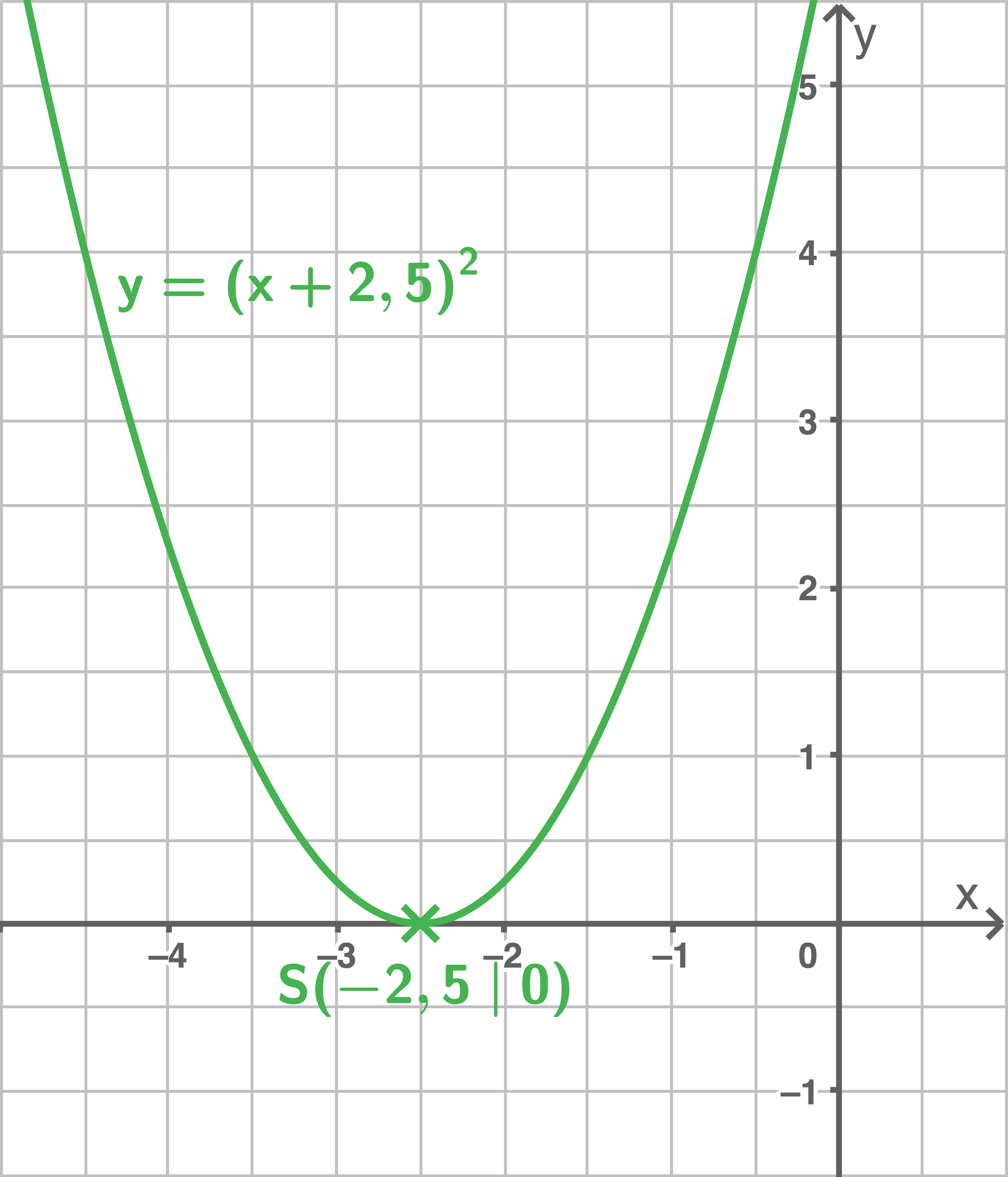
2
a)
b)
c)
d)