Quadratische Funktionen der Form y=x² (Normalparabel)
Eine quadratische Funktion ist eine Funktion der Form  mit dem Definitionsbereich
mit dem Definitionsbereich 
Der Graph dieser Funktion nennt sich Normalparabel. Die Normalparabel hat folgende Eigenschaften:
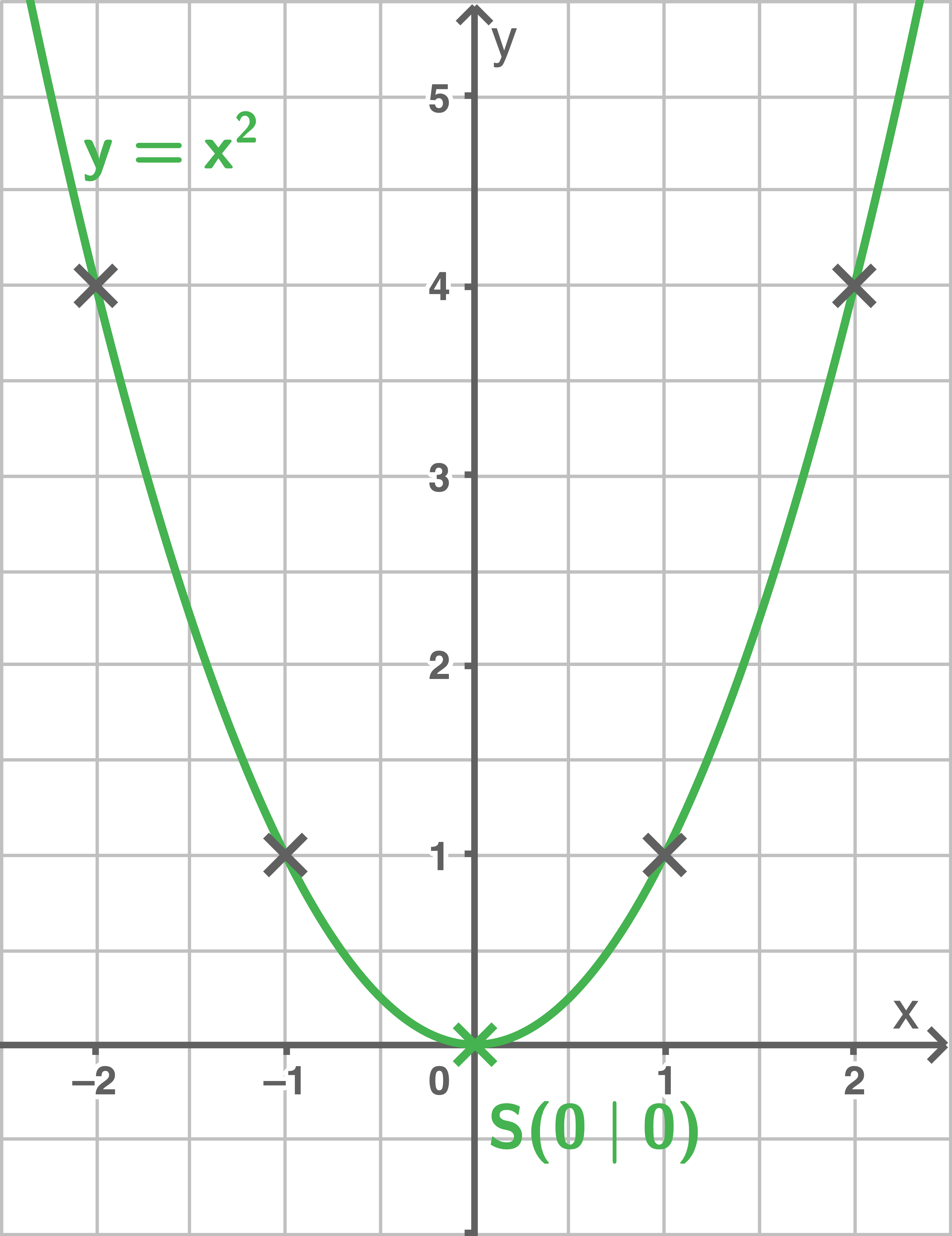
Der Graph dieser Funktion nennt sich Normalparabel. Die Normalparabel hat folgende Eigenschaften:
- Die Normalparabel ist symmetrisch zur
-Achse
- Der Scheitelpunkt
liegt im Koordinatenursprung und ist der tiefste Punkt
- Die Normalparabel ist nach oben geöffnet und fällt monoton für
und steigt monoton für
- Der Funktionswert kann alle Werte größer gleich Null annehmen, der sogennante Wertebereich umfasst also die Menge der reellen Zahlen größer gleich Null
- Einzige Nullstelle der Funktion ist

1
Die folgenden Punkte liegen auf einer Normalparabel. Bestimme die fehlende Koordinate.






2
Entscheide mit der Punktprobe, welche der Punkte auf der Normalparabel liegen und welche nicht.






Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2