Analysis 2.2 – Blutzucker

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=(x-2)^2 \cdot \mathrm{e}^{x+a} ; a \in \mathbb{R}.$
Der Graph von $f_a$ wird mit $G_a$ bezeichnet.
In der Abbildung 1 ist der Graph der ersten Ableitungsfunktion $\(f_0$ von $f_0$ dargestellt.

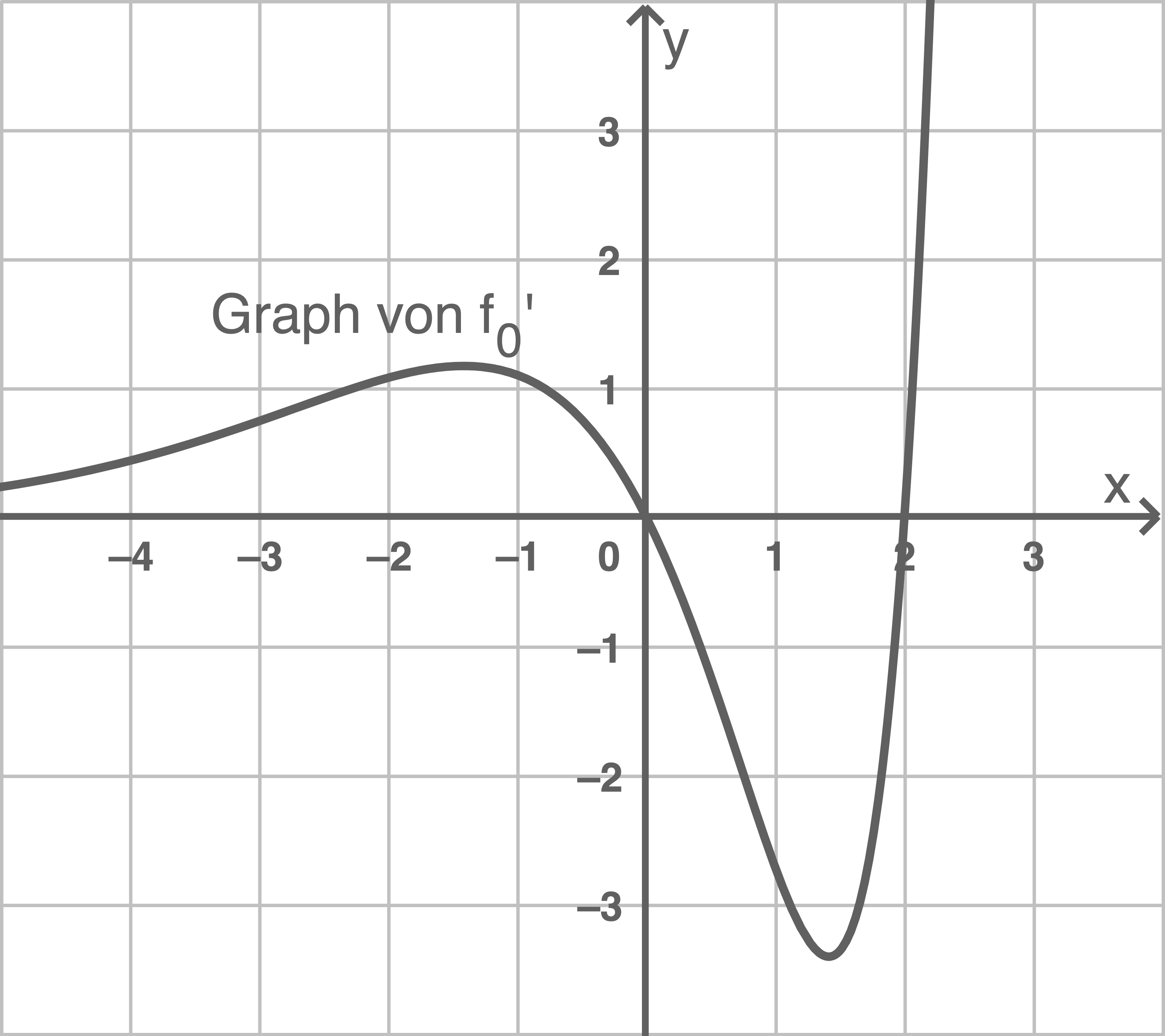
Graph von f' in einem Koordinatensystem mit Achsenbeschriftungen.

Abb. 1

Gib die Intervalle an, in denen $f_0$ monoton steigend ist.

(2 BE)

Berechne den Wert des Integrals $\(\displaystyle\int_{-1}^1 f_0$ und interpretiere diesen geometrisch als Flächenbilanz des Graphen von $\(f_0$

(2 BE)

Für einen Wert von $a$ ist $t(x)=8 x+32$ eine Gleichung der Tangente an $G_a$ im Punkt $A\left(-2 \mid f_a(-2)\right).$ Ermittle diesen Wert von $a$ und die Anzahl der zur Tangente $t$ echt parallel verlaufender Tangenten an diesen Graphen.

(4 BE)

Weise nach, dass für die erste Ableitungsfunktion $\(f_a$ gilt: $\(f_a$ und gib den Wert für $k$ an.

(2 BE)

Begründe unter Zuhilfenahme der Teilaufgabe d und der Abbildung 1, jedoch ohne Rechnung, dass folgende Aussage wahr ist:

Alle Graphen von $f_a$ haben genau einen Tiefpunkt $T\left(2 \mid f_a(2)\right)$ und genau einen Hochpunkt $H\left(0 \mid f_a(0)\right).$

(5 BE)

Der Graph der ersten Ableitungsfunktion $\(f_a$ die $x$ -Achse und die Geraden $x=-1$ und $x=1$ begrenzen eine Fläche, die sich aus zwei Flächenstücken zusammensetzt. Berechne den Parameterwert $a$ so, dass der Inhalt dieser Fläche den Wert $-\text{e}^4+8 \text{e}^3-9 \text{e}^2$ hat.

(4 BE)

Die Konzentration von Glukose im Blut wird als Blutzucker bezeichnet. Bei einem Patienten werden innerhalb der ersten vier Stunden nach der Nahrungsaufnahme die Blutzuckerwerte kontrolliert.
Die in $\mathbb{R}$ definierte Funktion $h$ mit $h(t)=40 t^2 \cdot \text{e}^{1-t}+90$ beschreibt für $0 \leq t \leq 4$ die zeitliche Entwicklung der Blutzuckerwerte. Dabei ist $t$ die seit der Nahrungsaufnahme vergangene Zeit in Stunden und $h(t)$ der Blutzuckerwert in Milligramm pro Deziliter.

Zu einem Zeitpunkt $t$ mit $t\gt0$ ist der Blutzuckerwert maximal.
Bestimme diesen maximalen Blutzuckerwert des Patienten

Hinweis: Auf die Untersuchung der Randwerte wird verzichtet.

(3 BE)

Ermittle, nach wie vielen Minuten der Blutzuckerwert auf $100$ Milligramm pro Deziliter gestiegen ist.

(2 BE)

Berechne den Wert des Terms $\frac{1}{2} \cdot\left(h(4)-h(2)\right)$ und interpretiere diesen im Sachzusammenhang.

(3 BE)

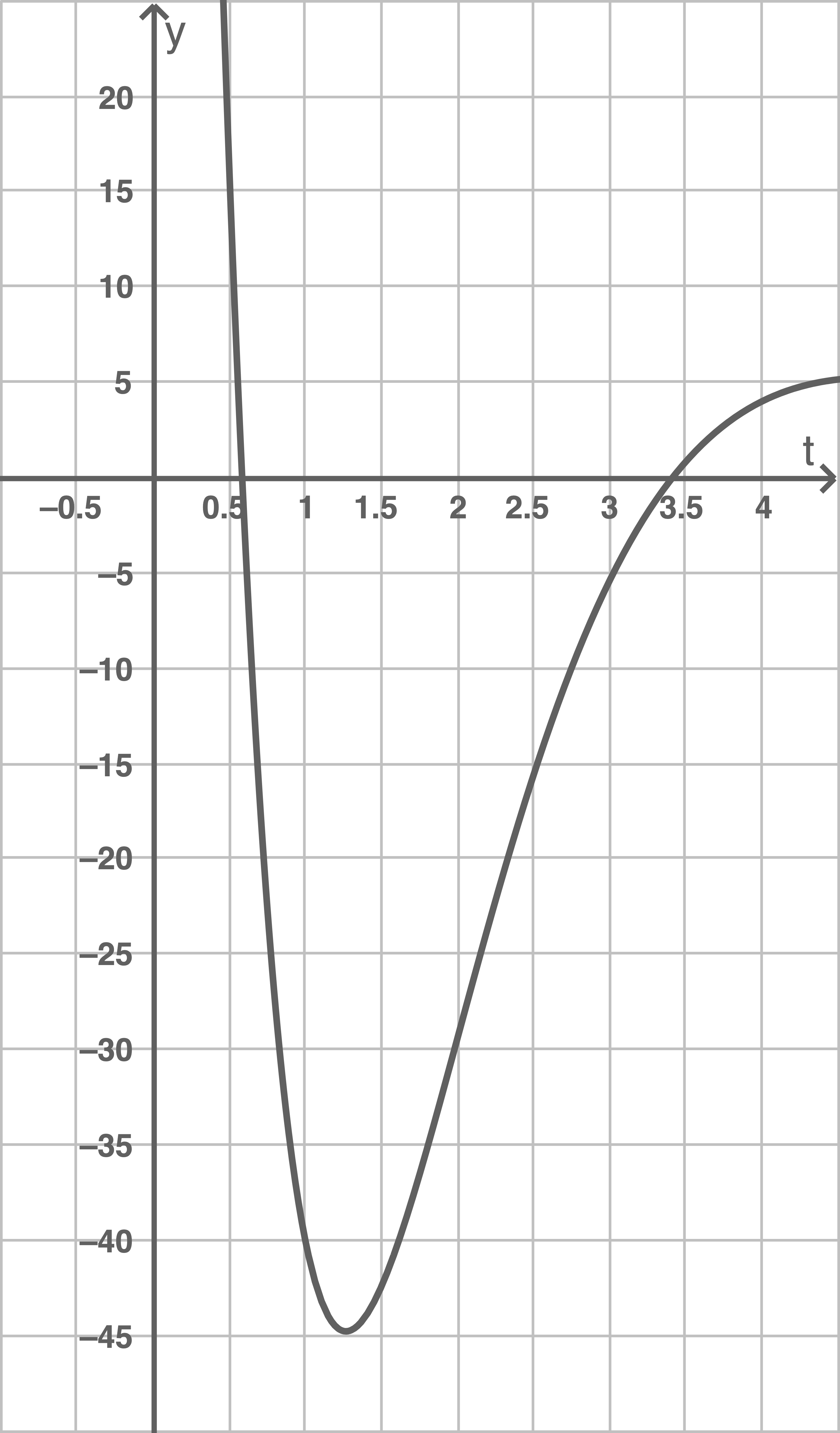
Die Abbildung 2 stellt den Graphen der zweiten Ableitungsfunktion von $h$ dar.
Gib unter Zuhilfenahme der Abbildung 2 näherungsweise den Zeitpunkt der maximalen Zuwachsrate des Blutzuckerwertes an.
Begründe deine Angabe.

Graph einer Funktion mit Achsenbeschriftungen y und t, zeigt eine Kurve mit einem Minimum.

Abb. 2

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$]-\infty ; 0]$ und $[2 ;+\infty[$

Wert berechnen

$\(\begin{array}[t]{rlll} \displaystyle\int_{-1}^{1}f_0$

Wert geometrisch interpretieren

Der Teil der Fläche, die der Graph von $f_0$ zwischen $x=-1$ und $x=1$ mit der $x$ -Achse einschließt, welcher unterhalb der $x$ -Achse liegt, ist größer als der darüberliegende.

Mit dem MMS folgt für die erste Ableitung von $f_a:$

$\(f_a$

Auflösen von $\(f_a$ nach $a$ mit dem solve-Befehl des MMS liefert:

$a=2$

Mit dem solve-Befehl des MMS ergibt sich aus $\(f_2$ weiter:

$\begin{array}[t]{rlll} x_1&=&-2 \\[5pt] x_2&\approx&-0,95 \\[5pt] x_3&\approx&2,07 \end{array}$

Somit gibt es zwei Tangenten an $G_a,$ die zu $t$ parallel verlaufen.

$\(\begin{array}[t]{rlll} f_a$

Der gesuchte Wert von $k$ ist somit $k=\mathrm e^a.$

Es gilt stets $\mathrm e^a\gt0,$ das heißt, da nach Teilaufgabe d die Gleichung $\(f_a$ gilt, besitzen alle Funktionen der Schar $f_a$ das gleiche Monotonieverhalten. Somit sind die Extremstellen von $f_a$ durch die Nullstellen von $\(f_a$ gegeben, welche widerum durch die Nullstellen von $f_0$ gegeben sind, da die $\mathrm e$ -Funktion stets ungleich Null ist.
Da der Graph von $\(f_0$ bei $x=0$ einen Vorzeichenwechsel von Plus zu Minus hat, ist somit $T\left(2 \mid f_a(2)\right)$ der einzige Tiefpunkt aller Graphen von $f_a.$
Da der Graph von $\(f_0$ bei $x=2$ einen Vorzeichenwechsel von Mius zu Plus hat, ist somit $H\left(0 \mid f_a(0)\right)$ der einzige Hochpunkt aller Graphen von $f_a.$

Mit der graphischen Darstellung des MMS folgt, dass die Teilfläche links von $x=0$ oberhalb der $x$ -Achse liegt, während die Teilfläche rechts der Null unterhalb der $x$ -Achse liegt. Somit ergibt sich folgende Gleichung:

Gleichung anzeigen

Auflösen nach $a$ mit dem solve-Befehl des MMS liefert $a=3.$

Für die erste Ableitung von $h$ folgt mit dem MMS:

$\(h$

Anwenden der notwendigen Bedingung für Extremstellen $\(h$ liefert mit dem solve-Befehl des MMS:

$\begin{array}[t]{rlll} t_1&=&0 \\[5pt] t_2&=&2 \end{array}$

Da der Blutzucker zu einem Zeitpunkt $t\gt0$ maximal ist, ist $t_2$ der gesuchte Wert. Einsetzen in $h(t)$ liefert:

$\begin{array}[t]{rlll} h(2)&=&40\cdot2^2\cdot\mathrm e^{1-2}+90 \\[5pt] &=&160\mathrm e^{-1}+90 \\[5pt] &\approx&148,9 \end{array}$

Der maximale Blutzuckerwert des Patienten beträgt somit $148,9$ Milligramm pro Deziliter.

$\begin{array}[t]{rlll} h(t)&=&100 \\[5pt] 40 t^2 \cdot \mathrm e^{1-t}+90&=&100 \end{array}$

Mit dem solve-Befehl des MMS folgt:

$\begin{array}[t]{rlll} t_1&\approx&-0,27 \\[5pt] t_2&\approx&0,36 \\[5pt] t_3&\approx&5,95 \end{array}$

Da $0\leq t\leq4$ gilt, folgt $t_2$ als die gesuchte Lösung. Damit ergibt sich, dass der Blutzuckerwert nach ca. $0,36\cdot60\approx22$ Minuten auf $100$ Milligramm pro Deziliter gestiegen ist.

Wert berechnen

Rechenweg anzeigen

$\dfrac{1}{2} \cdot(h(4)-h(2)) \approx -13,5$

Wert im Sachzusammenhang interpretieren

In den letzten zwei Stunden nimmt der Blutzuckerwert des Patienten im Durchschnitt mit einer Rate von ca. $13,5$ Milligramm pro Deziliter pro Stunde ab.

Eine Nullstelle der zweiten Ableitungsfunktion mit einem Vorzeichenwechsel von Plus zu Minus entspricht einer Hochstelle der ersten Ableitungsfunktion.
Somit nimmt der Blutzuckerwert des Patienten nach ca. $0,6$ Stunden am stärksten zu.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?