Wahlteil B2
B2 Analytische Geometrie
In einem kartesischen Koordinatensystem kann die Lage der Startbahn eines Flughafens folgendermaßen beschrieben werden: Die
2.1
Berechne den Steigungswinkel von Flugzeug  auf dem Weg von
auf dem Weg von  nach
nach  .
.
2.2
Zum selben Zeitpunkt, in dem sich das Flugzeug  im Punkt
im Punkt  befindet, passiert Flugzeug
befindet, passiert Flugzeug  den Punkt
den Punkt  .
Untersuche, nach welcher Zeit beide Flugzeuge die gleiche Flughöhe haben, wenn man voraussetzt, dass sich beide mit einer konstanten Geschwindigkeit von
.
Untersuche, nach welcher Zeit beide Flugzeuge die gleiche Flughöhe haben, wenn man voraussetzt, dass sich beide mit einer konstanten Geschwindigkeit von  bewegen.
bewegen.
2.3
Bestimme die kürzeste Entfernung des zweiten Flugzeuges zur Spitze des Sendemastes.
2.4
Begründe, dass der Punkt  auf der Startbahn liegt.
Gäste auf der Besucherterasse des Flughafengebäudes haben den start vin Flugzeig
auf der Startbahn liegt.
Gäste auf der Besucherterasse des Flughafengebäudes haben den start vin Flugzeig  beobachtet. Es war deutlich zu erkennen, dass das Flugzeug vom Abheben von der Startbahn bis zum Punkt
beobachtet. Es war deutlich zu erkennen, dass das Flugzeug vom Abheben von der Startbahn bis zum Punkt  deutlich steiler aufgestiegen ist als später von
deutlich steiler aufgestiegen ist als später von  nach
nach  .
.
Ein Gast behauptet: „ Das war‘n ja mindestens Grad“.
Überprüfe diese Behauptung.
Später hat sich ein drittes Flugzeug von dieser Startbahn vom Startpunkt
Grad“.
Überprüfe diese Behauptung.
Später hat sich ein drittes Flugzeug von dieser Startbahn vom Startpunkt  aus mit einem konstanten Steigungswinkel von
aus mit einem konstanten Steigungswinkel von  zum Punkt
zum Punkt  bewegt. Bestimme die Koordinaten von
bewegt. Bestimme die Koordinaten von  .
.
Ein Gast behauptet: „ Das war‘n ja mindestens
2.5
Die Besucherterrasse wird von einem Sonnensegel in Dreiecksform beschattet. Bei leerer Terrasse fällt der Schatten des Segels vollständig auf den Terrassenboden. Der Boden liegt in der Ebene  mit der Gleichung:
mit der Gleichung:  . Die Eckpunkte des Sonnensegels befinden sich in den Punkten
. Die Eckpunkte des Sonnensegels befinden sich in den Punkten
 ,
, 
 ,
, 
 .
Die Sonnenstrahlen verlaufen in Richtung
.
Die Sonnenstrahlen verlaufen in Richtung  -
Berechne die Größe des Sonnensegels in
-
Berechne die Größe des Sonnensegels in  .
.
Vergleiche diese Größe mit der Größe des Schattens des Sonnensegels.
Vergleiche diese Größe mit der Größe des Schattens des Sonnensegels.
B2 Analytische Geometrie
2.1
Stelle also die Gleichung einer Gerade
2.2
2.3
- Stelle die Gleichung einer Hilfsebene
auf, die senkrecht auf
steht und
enthält.
- Berechne die Koordinaten des Schnittpunkts
von
und
. Dies ist der Fußpunkt des Lotes von
auf
.
- Berechne die Länge der Strecke
.
2.4
Zudem liegt die Startbahn auf dem Boden, also innerhalb der
Der Punkt
Die Startbahn ist
Den Abstand zwischen dem Punkt
- Stelle die Koordinaten aller Punkte
auf der Startbahn in Abhängigkeit eines Parameters
auf.
- Bilde mit Hilfe dieser Koordinaten den Verbindungsvektor
- Setze diesen Verbindungvektor zusammen mit dem geforderten Winkel
in die Formel für den Steigungswinkel ein. So erhältst du eine Gleichung in Abhängigkeit von
, die du lösen kannst.
Diese Gleichung kannst du mit dem solve-Befehl deines CAS lösen. Du erhältst dann folgendes Ergebnis:

 Für
Für  liegt
liegt  allerdings nicht mehr auf der Startbahn. Es muss also
allerdings nicht mehr auf der Startbahn. Es muss also  gelten. Der Startpunkt hat damit die Koordinaten
gelten. Der Startpunkt hat damit die Koordinaten  .
.
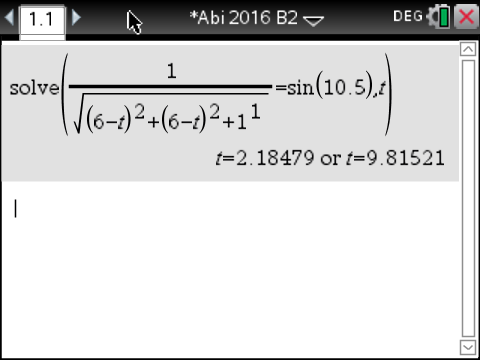 Abb. 1: Gleichung lösen
Abb. 1: Gleichung lösen
2.5
- Stelle für jeden Punkt
,
und
die Gleichung der Schattengerade auf, entlang welcher die Sonnenstrahlen verlaufen. Diese Gerade verläuft durch den jeweiligen Punkt in Richtung der Sonnenstrahlen.
- Die Schnittpunkte der Geraden mit der Ebene
, in der der Terrassenboden liegt, sind die Schattenpunkte der Eckpunkte.
- Berechne mit der Formel aus dem vorherigen Aufgabenteil die Größe des Schattens.
- Vergleiche die beiden Größen miteinander, indem du berechnest, um wie viel
die Fläche des Schattens größer bzw. kleiner ist als die des Sonnensegels.
© 2017 - SchulLV.
B2 Analytische Geometrie
2.1
Stelle also die Gleichung einer Gerade
2.2
2.3
- Stelle die Gleichung einer Hilfsebene
auf, die senkrecht auf
steht und
enthält.
- Berechne die Koordinaten des Schnittpunkts
von
und
. Dies ist der Fußpunkt des Lotes von
auf
.
- Berechne die Länge der Strecke
.
2.4
Zudem liegt die Startbahn auf dem Boden, also innerhalb der
Der Punkt
Die Startbahn ist
Den Abstand zwischen dem Punkt
- Stelle die Koordinaten aller Punkte
auf der Startbahn in Abhängigkeit eines Parameters
auf.
- Bilde mit Hilfe dieser Koordinaten den Verbindungsvektor
- Setze diesen Verbindungvektor zusammen mit dem geforderten Winkel
in die Formel für den Steigungswinkel ein. So erhältst du eine Gleichung in Abhängigkeit von
, die du lösen kannst.
Diese Gleichung kannst du mit dem solve-Befehl deines CAS lösen. Du erhältst dann folgendes Ergebnis:

 Für
Für  liegt
liegt  allerdings nicht mehr auf der Startbahn. Es muss also
allerdings nicht mehr auf der Startbahn. Es muss also  gelten. Der Startpunkt hat damit die Koordinaten
gelten. Der Startpunkt hat damit die Koordinaten  .
.
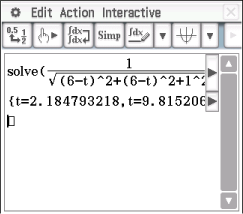 Abb. 1: Gleichung lösen
Abb. 1: Gleichung lösen
2.5
- Stelle für jeden Punkt
,
und
die Gleichung der Schattengerade auf, entlang welcher die Sonnenstrahlen verlaufen. Diese Gerade verläuft durch den jeweiligen Punkt in Richtung der Sonnenstrahlen.
- Die Schnittpunkte der Geraden mit der Ebene
, in der der Terrassenboden liegt, sind die Schattenpunkte der Eckpunkte.
- Berechne mit der Formel aus dem vorherigen Aufgabenteil die Größe des Schattens.
- Vergleiche die beiden Größen miteinander, indem du berechnest, um wie viel
die Fläche des Schattens größer bzw. kleiner ist als die des Sonnensegels.
© 2017 - SchulLV.