Wahlteil A3

A3 Analysis und Stochastik

3.1

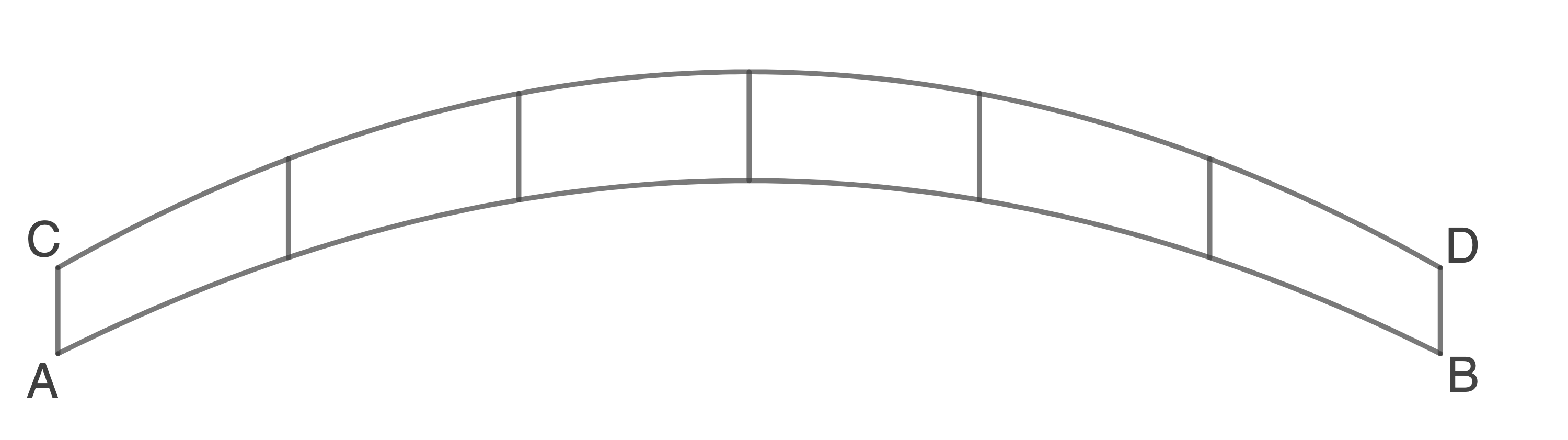
Auf Flusskreuzfahrten legen die Fahrgastschiffe oftmals in Städten an, um ihren Passagieren Landgänge zu ermöglichen. Die Distanz zwischen Schiff und Ufer wird durch eine Gangway überbrückt. Die Skizze veranschaulicht die Seitenansicht einer Gangway. Der Bogen von $A$ bis $B$ wird durch einen Teil der Parabel $p_1,$ der obere Bogen von $C$ bis $D$ durch einen Teil der Parabel $p_2$ beschrieben. Dabei modelliert $p_1$ den Verlauf des Fußweges, welchen die Passagiere benutzen, und $p_2$ den Verlauf eines Handlaufs oben am Geländer. Zwischen den Streben $AC$ und $BD$ gibt es weitere fünf zu diesen beiden parallele Streben. Die Abstände benachbarter Streben sind jeweils gleich.

Grafische Darstellung eines gebogenen Objekts mit den Beschriftungen A, B, C und D.

Die Parabeln haben in einem geeigneten Koordinatensystem folgende Gleichungen:

$p_1: f(x)=-0,0414x^2+0,5x$
$p_2: h(x)=-0,0469x^2+0,5664x+0,75$

In diesem Koordinatensystem liegen die Punkte $A$ und $B$ auf der $x$ -Achse. Die Strecke $BD$ verläuft parallel zur $y$ -Achse. Eine Längeneinheit beträgt $1\,\text{m}.$

Es wird angenommen, dass die Gangway im Punkt $A$ auf dem Schiff aufliegt und im Punkt $B$ auf dem Ufer.

3.1.1

Die Endpunkte $A$ und $B$ der Gangway befinden sich auf gleicher Höhe.

Berechne die Spannweite der Gangway.
Bestimme den Höhenunterschied, den die Passagiere beim Verlassen des Schiffes überwinden müssen.
Ermittle die Gesamtlänge aller Streben auf beiden Seiten des Geländers.

(9 BE)

3.1.2

Beide Seiten der Gangway wurden außen vollständig mit Kunststoffplanen verkleidet.

Berechne die Fläche des dafür verwendeten Ausgangsmaterials, wenn bei der Herstellung $15\%$ Verschnitt und Überlappung auftraten.

(4 BE)

3.1.3

Der durch $p_1$ modellierte Bogen wurde aus einem geraden Stahlrohr geformt.

Untersuche, ob ein $12,3\,\text{m}$ langes Stahlrohr dafür ausreichend war.

(3 BE)

3.1.4

Manchmal befindet sich der Endpunkt $A$ der Gangway tiefer als der Punkt $B.$ Aus Sicherheitsgründen darf der den Passagieren zugemutete Höhenwinkel beim Überwinden der Gangway nicht größer als $35^{\circ}$ sein.

Berechne den maximal zulässigen Höhenunterschied zwischen $A$ und $B$ , wenn die volle Länge der Gangway genutzt wird.

(5 BE)

3.2

Auf dem Schiff wird zur Unterhaltung ein Glücksspiel angeboten. Der Spieler wirft gleichzeitig zwei ideale Würfel, die jeweils die Augenzahlen $1$ bis $6$ tragen, und addiert die beiden Augenzahlen.

3.2.1

Für die Summe der Augenzahlen und die jeweiligen Wahrscheinlichkeiten wird die Zufallsgröße $X$ verwendet.

$x_i$	$P(X=x_i)$
$2$	$\frac{1}{36}$
$3$	$\frac{2}{36}$
$4$	$\frac{3}{36}$
$5$	$\frac{4}{36}$
$6$	$\frac{5}{36}$
$7$
$8$	$\frac{5}{36}$
$9$	$\frac{4}{36}$
$10$	$\frac{3}{36}$
$11$	$\frac{2}{36}$
$12$

Gib die in der Tabelle fehlenden Wahrscheinlichkeiten an.
Begründe.

(3 BE)

3.2.2

Bei diesem Spiel gewinnt der Spieler, wenn die Augensumme eine Primzahl außer „ $7$ “ ist. Der Gewinn entspricht dieser Summe. Der Einsatz pro Spiel beträgt $2,00\,€.$
Untersuche, ob dieses Spiel fair ist.

Ermittle, auf wie viel Euro der Betreiber des Spiels den Einsatz erhöhen muss, wenn er zu den bisherigen Gewinnzahlen noch die „ $7$ “ zulassen und bei einer großen Zahl von Spielen durchschnittlich pro Spiel mindestens $40$ Cent verdienen will.

(6 BE)

3.2.3

Die für das Spiel notwendigen Würfel werden jeweils am Spieltag einer größeren Kisten einzeln zufällig entnommen. An einem Sonnabend befinden sich in der Kiste genau $1000$ Würfel und zwar $500$ blaue, $400$ weiße sowie nur noch rote.

Bestimme die Wahrscheinlichkeiten dafür, dass unter $20$ entnommenen Würfeln

genau $3$ rote
mehr als $3$ rote Würfel sind.

Gib an, wie viele Würfel der Kiste mindestens entnommen werden müssen, damit unter ihnen garantiert ein roter Würfel ist.

(5 BE)

3.1.1

Berechne die Nullstellen von $f(x):$

$\begin{array}[t]{rll} 0&=& f(x) &\quad \\[5pt] 0&=& -0,0414x^2+0,5x &\quad \scriptsize \mid\;:(-0,0414) \\[5pt] 0&=&x^2-\dfrac{2500}{207}x &\quad \scriptsize \mid\;pq-\text{Formel} \\[5pt] x_{1,2}&=& -\dfrac{(-\frac{2500}{207})}{2} \pm \sqrt{\left(\dfrac{-\frac{2500}{207}}{2}\right)^2} \\[5pt] x_{1,2}&=&\dfrac{1250}{207}\pm\dfrac{1250}{207} \end{array}$

$x_{1}=0$

$x_{2}= \frac{2500}{207} \approx 12,08$

Die Gangway hat also eine Spannweite von ca. $12\,\text{m}.$

Der zu überwindende Höhenunterschied ist die $y$ -Koordinate des Scheitelpunktes von $p_1$ , die sich als Funktionswert an der Mittelstelle $x_s=\dfrac{x_{1}+x_{2}}{2}$ der Nullstellen ergibt:

$y=f(x_s)=f\left(\frac{1250}{207}\right)\approx 1,51$

Die Passgiere müssen also ca. $1,5 \,\text{m}$ überwinden.

Die Strebe an der Stelle $x_i$ hat die Länge $s(x_i)=h(x_i)-f(x_i).$
Die Stellen, an denen sich die Streben befinden, lauten:

$x_i=x_{1}+\dfrac{i}{6}\cdot (x_{2}-x_{1})\;,\quad i=0,1,...,6$

Ermittle mit deinem CAS Taschenrrechner:

$x_0=0\;,\;x_1=\frac{1250}{621}\;,\;x_2=\frac{2500}{621}\;,\;$ $x_3=\frac{1250}{207}\;,\; x_4=\frac{5000}{621}\;,\;x_5=\frac{6250}{621}\;,\;$ $x_6=\frac{2500}{207}$

Also ist die Gesamtstrebenlänge (auf beiden Seiten der Gangway), löse mit der Solve-Funktion deines CAS Taschenrechners:

$s(x_i)=-0,0055x_i^2+0,0664x_i+0,75$

$2\cdot \left( s(x_0)+s(x_1)+s(x_2)+s(x_3)+s(x_4)+s(x_5)+s(x_6) \right)\approx 12,1 \,\text{m}$

3.1.2

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$A_{Plane}=2 \cdot \displaystyle\int_{0}^{12}\left(h(x)-f(x)\right) \mathrm dx \approx 21,2$

$A_{Ausgang}= A_{Plane}\cdot 1,15 \approx 24,4$
Das Ausgangsmaterial muss also ca. $24\,\text{m}^2$ groß gewesen sein.

Die Aufgabenstellung erlaubt auch die Interpretation $A_{Ausgang}=\dfrac{A_{Plane}}{0,85}.$

3.1.3

Der Bogen $p_1$ ist sicherlich länger als die gerade Verbindung von $A$ und $B$ über den Scheitelpunkt $\left(x_s=\frac{1250}{207}\right)$ von $p_1.$ Dieser Streckenzug hat aufgrund der Symmetrie die Länge:

$l=2\cdot \sqrt{(x_s)^2+ \left( f(x_s) \right)^2} \approx 12,45 \gt 12,3$

Ein $12,3\,\text{m}$ langes Stahlrohr reicht also nicht für $p_1.$

3.1.4

$p_1$ hat seinen maximalen Steigungswinkel in $A$ , nämlich

$\(\alpha=\arctan\left(f$

Der maximale Gesamtwinkel ist $35^{\circ},$ also darf $\overline{AB}$ höchstens einen Steigungswinkel von $35^{\circ}-26,6^{\circ}=8,4^{\circ}$ haben. Folglich darf sich $B$ maximal $\Delta y=12,08 \cdot \sin(8,4^{\circ}) \approx 1,8 \,\text{m}$ über $A$ befinden.

3.2.1