Pflichtaufgaben

1 Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{1}{4} x^3-3 x.$

1.1

Es gilt $\(f$ Zeige, dass $2$ eine Extremstelle von $f$ ist.

(2 BE)

1.2

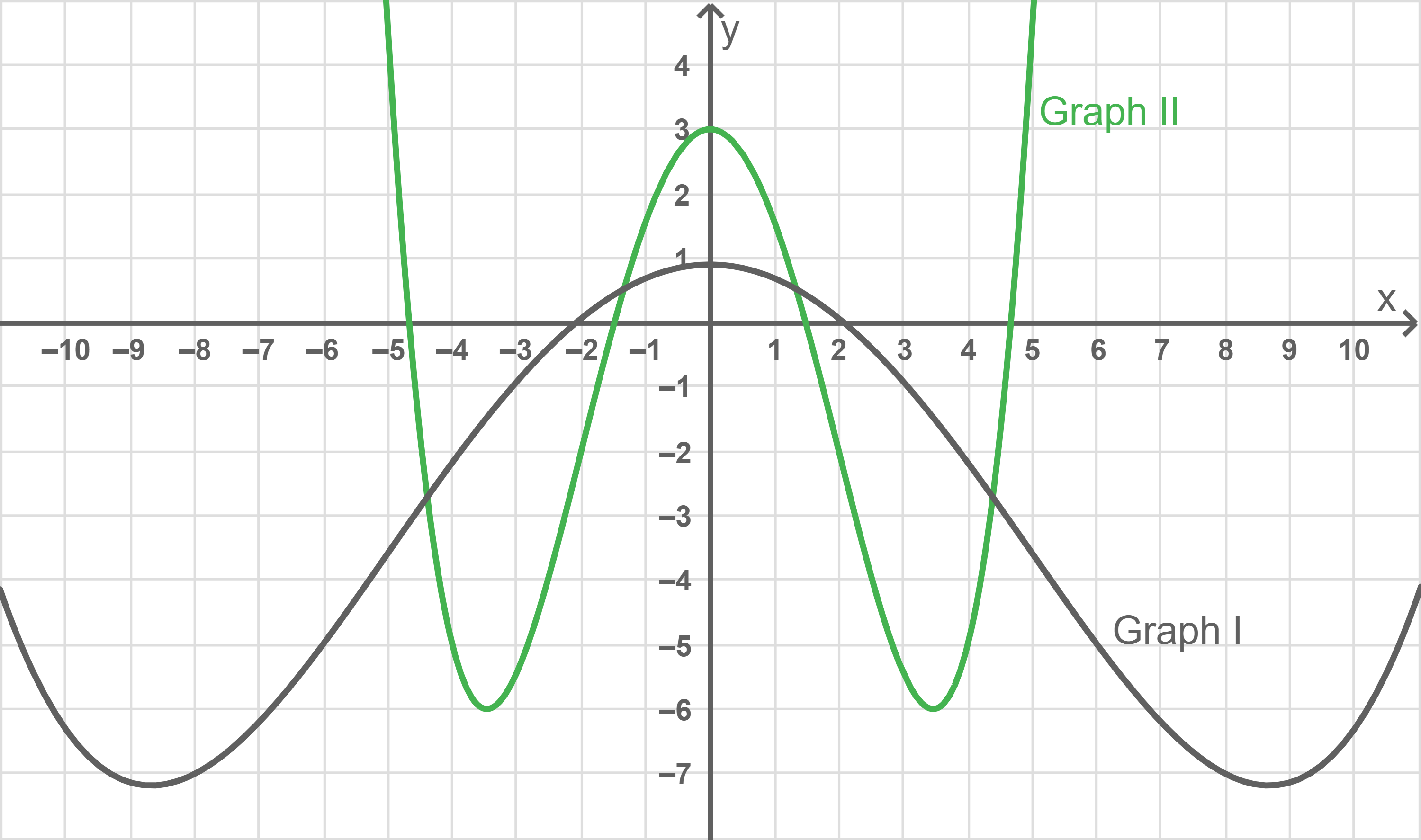
Einer der abgebildeten Graphen I und II ist der Graph einer Stammfunktion von $f.$

Gib diesen Graphen an und begründe deine Angabe.

(3 BE)

2 Analysis

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=3 \cdot \cos (x).$

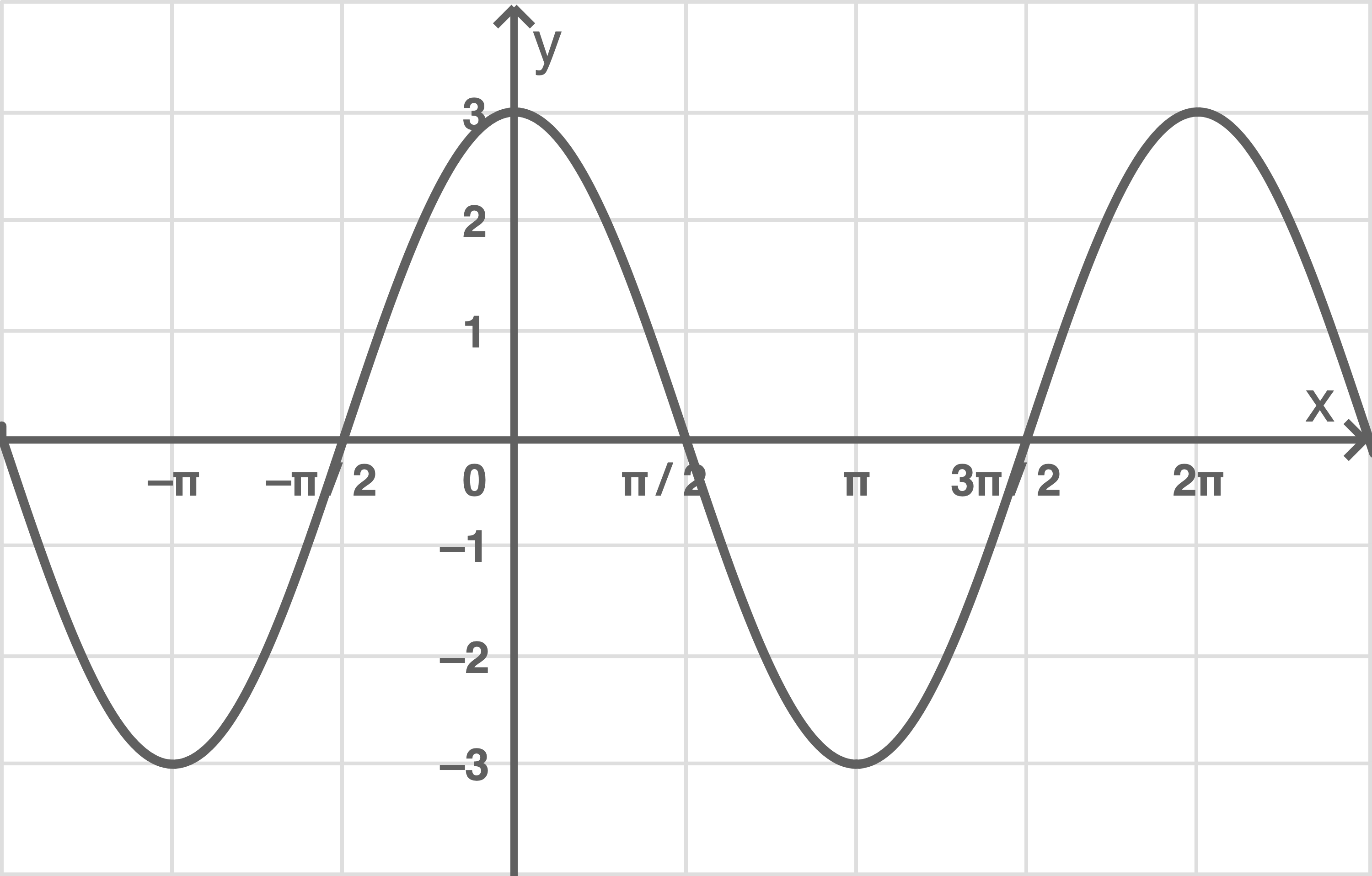
Graph einer Sinusfunktion mit Achsenbeschriftungen für x und y.

2.1

Gib den Wert des Integrals $\displaystyle\int_{0}^{\pi}f(x)\;\mathrm dx$ an.

(1 BE)

2.2

Die in $\mathbb{R}$ definierte Funktion $g$ ist gegeben durch $g(x)=a \cdot f(x)+b \cdot x$ mit reellen Zahlen $a$ und $b$ . Die Punkte $(0 \mid-3)$ und $\left(\frac{\pi}{2} \left\lvert\, \frac{3}{4} \pi\right.\right)$ liegen auf dem Graphen von $g.$

Ermittle $a$ und $b.$

(4 BE)

3 Analytische Geometrie

Gegeben sind die Punkte $A(6\mid-1\mid 2), B$ und $C(2\mid-1\mid 6)$ sowie der Vektor $\overrightarrow{AB}=\pmatrix{-4\\4\\0}.$

3.1

Gib die Koordinaten des Punktes $B$ an.

(1 BE)

3.2

In der $yz$ -Ebene existiert ein Punkt $P,$ für den $\overrightarrow{A B} \mid\mid \overrightarrow{C P}$ gilt.

Bestimme die Koordinaten von $P.$

(4 BE)

4 Stochastik

Vier Freunde bewerben sich um die Teilnahme an einer TV-Show. Von den insgesamt $4000$ Bewerbenden werden $1000$ zufällig für die Teilnahme an der Show ausgewählt.

Die Zufallsgröße $X$ beschreibt, wie viele der vier Freunde ausgewählt werden.

4.1

Begründe, dass die Annahme gerechtfertigt ist, $X$ als binomialverteilt zu modellieren.

(2 BE)

4.2

Gib den Erwartungswert von $X$ an.

(1 BE)

4.3

Bestimme die Wahrscheinlichkeit dafür, dass mindestens einer der Freunde für die Teilnahme an der Show ausgewählt wird.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?