Wahlteil A2

Analytische Geometrie

Gegeben ist eine Pyramide $ABCS$ . Ihre Grundfläche ist das Dreieck $ABC$ . Ihre Punkte haben in einem kartesischen Koordinatensystem die Koordinaten

$A(6\mid 2\mid 1)$ , $B(6\mid8\mid1)$ , $C(2\mid5\mid3)$ und $S(8\mid5\mid10)$ .

2.1

Stelle die Pyramide $ABCS$ in einem Koordinatensystem dar.

2.2

Prüfe, ob folgende Aussagen wahr sind.

Das Dreieck $ABC$ ist rechtwinklig.
Das Dreieck $ABC$ ist gleichschenklig.
Der Punkt $P(0\mid6,5\mid4)$ liegt auf der Dreiecksseite $\overline{AC}$ .

2.3

Gib eine Koordinatengleichung für die Ebene $\varepsilon_1$ an, in der das Dreieck $ABC$ liegt.

2.4

Der Punkt $S$ wird an $\varepsilon_1$ gespiegelt.

Bestimme die Koordinaten des Bildpunktes $S‘$ .

2.5

Ermittle den Neigungswinkel der Seitenfläche $ABS$ gegenüber der Grundfläche der Pyramide.

2.6

Eine zur $xy-$ Ebene parallele Ebene $\varepsilon_2$ verläuft durch den Punkt $C$ .

Bestimme den Inhalt der Schnittfläche von $\varepsilon_2$ mit der Pyramide.

2.7

Berechne das Volumen der Pyramide.

2.8

Der Punkt $D$ liegt auf der Kante $\overline{SC}$ .
Bestimme die Koordinaten von $D$ so, dass die Ebene durch die Punkte $A$ , $B$ und $D$ die Pyramide in zwei volumengleiche Körper teilt.

(35P)

2.1

$\blacktriangleright$ Pyramide dreidimensional darstellen

In diesem Aufgabenteil sollst du die Pyramide mit den Eckpunkten $A(6 \mid 2 \mid 1), \, B(6 \mid 8 \mid 1), \, C(2 \mid 5 \mid 3)$ und $S(8 \mid 5 \mid 10)$ in einem Koordinatensystem darstellen.

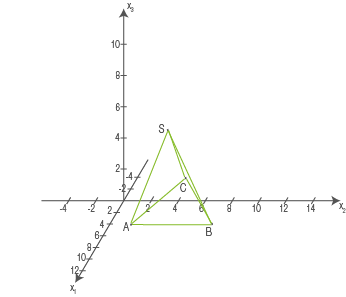Graph mit Koordinatensystem und einem grünen Dreieck ABC.

Abb. 1: Darstellung der Pyramide $ABCS$

2.2

$\blacktriangleright$ Wahrheit dreier Aussagen prüfen

Du sollst prüfen, ob eine der drei folgenden Aussagen zutrifft:

Das Dreieck $ABC$ ist rechtwinklig
Das Dreieck $ABC$ ist gleichschenklig
Der Punkt $P(O \mid 6,5 \mid 4)$ liegt auf der Dreieckseite zwischen $A$ und $C$

$\blacktriangleright$ Rechtwinkligkeit prüfen

Du sollst überprüfen, ob es sich bei dem Dreieck $ABC$ um ein rechtwinkliges Dreieck handelt. Dazu kannst du das Skalarprodukt zweier Vektoren verwenden.

Betrachte die Vektoren $\overrightarrow{AB}$ , $\overrightarrow{AC}$ und $\overrightarrow{BC}$ , die den Verlauf der Seiten des Dreiecks beschreiben. Das Skalarprodukt zweier senkrechter Vektoren $\overrightarrow{a}$ , $\overrightarrow{b}$ ergibt $0$ .

$\text{Stehen zwei Vektoren senkrecht aufeinander, so ist ihr Skalarprodukt Null.}$

Ist das Dreieck rechtwinklig, bedeutet dies also auch, dass das Skalarprodukt zweier Seitenvektoren Null ergibt, da diese dann einen rechten Winkel einschließen.

Berechne also zuerst diese Vektoren und prüfe anschließend, ob zwei davon senkrecht aufeinander stehen.

$\overrightarrow{AB} = \pmatrix{6\\8\\1} - \pmatrix{6\\2\\1} = \pmatrix{0\\6\\0}$

$\overrightarrow{AC} = \pmatrix{2\\5\\3} - \pmatrix{6\\2\\1} = \pmatrix{-4\\3\\2}$

$\overrightarrow{BC} = \pmatrix{2\\5\\3} - \pmatrix{6\\8\\1} = \pmatrix{-4\\-3\\2}$

Für diese Vektoren kannst du nun die Skalarprodukte $\overrightarrow{AB} \cdot \overrightarrow{AC}$ , $\overrightarrow{AC} \cdot \overrightarrow{BC}$ und $\overrightarrow{AB} \cdot \overrightarrow{BC}$ ausrechnen. Ist eines davon Null, so ist das Dreieck rechtwinklig.

$\overrightarrow{AB} \cdot \overrightarrow{AC} = 0 \cdot (-4) + 6 \cdot 3 + 0 \cdot 2 = 18$

$\overrightarrow{AC} \cdot \overrightarrow{BC} = (-4) \cdot (-4) + 3 \cdot (-3) + 2 \cdot 2 = 11$

$\overrightarrow{AB} \cdot \overrightarrow{BC} = 0 \cdot (-4) + 6 \cdot (-3) + 0 \cdot 2 = -18$

Du erkennst, dass jedes einzelne dieser Skalarprodukte ungleich $0$ ist. Demzufolge ist das Dreieck $ABC$ nicht rechtwinklig.

$\blacktriangleright$ Gleichschenkligkeit prüfen

Um nachzuweisen, ob das Dreieck $ABC$ gleichschenklig ist, betrachtest du die Beträge, also die Länge der Vektoren $\overrightarrow{AB}$ , $\overrightarrow{AC}$ und $\overrightarrow{BC}$ , die den Verlauf der Seiten des Dreiecks beschreiben. Bei einem gleichschenkligen Dreieck sind zwei dieser Beträge identisch, da zwei Seiten die gleiche Länge haben müssen. Den Betrag eines Vektors berechnest du mit folgender Formel

$\overrightarrow{a} = \sqrt{a_1^2+a_2^2+a_3^3}$

Berechne also die Länge der Seitenvektoren und vergleiche sie.

$\vert \overrightarrow{AB} \vert = \sqrt{6^2} = 6$

$\vert \overrightarrow{AC} \vert = \sqrt{(-4)^2 + 3^2 + (2)^2 } = \sqrt{29}$

$\vert \overrightarrow{BC} \vert = \sqrt{(-4)^2 + (-3)^2 + (2)^2 } = \sqrt{29}$

Da die Seitenvektoren $\overrightarrow{BC}$ und $\overrightarrow{AC}$ die gleiche Länge haben, ist das Dreieck $ABC$ gleichschenklig.

$\blacktriangleright$ Lage eines Punktes überprüfen

Du sollst prüfen, ob der Punkt $P(0 \mid 6,5 \mid 4)$ auf der Dreieckseite $\overline{AC}$ liegt. Dazu gehst du folgendermaßen vor:

Die Punkte auf der Dreieckseite liegen auf einer Geraden. Diese Gerade kannst du durch eine Gleichung darstellen, deren Richtungsvektor $\overrightarrow{AC}$ und deren Stützvektor $\overrightarrow{OA}$ entspricht. Mithilfe des Geradenparameters $r$ bestimmst du, ob der Punkt $P$ auf der Geraden liegt. Ist dies der Fall, überprüfst du ebenfalls mit Hilfe des Parameters, ob $P$ ziwschen den Punkten $A$ und $C$ liegt.

1. Schritt: Geradengleichung bestimmen

Mit den schon bestimmten Vektoren $\overrightarrow{AC}$ und $\overrightarrow{OA}$ erhältst du folgende Geradengleichung

Stelle also zunächst eine Gleichung für die Gerade $g$ auf, die durch die beiden Punkte $A$ und $C$ verläuft

$g: \overrightarrow{x} = \pmatrix{6\\2\\1} + r \cdot \pmatrix{-4\\3\\2}$

Darin ist $r$ ein reeler Parameter.

2. Schritt: Lage des Punktes $P$ auf der Geraden überprüfen

Wenn der Punkt $P$ auf dieser Geraden liegt, so ist das Gleichungssystem $\overrightarrow{OP} = \overrightarrow{x}$

für $r$ eindeutig lösbar, das heißt, es existiert nur eine einzige Lösung für $r$ . Stelle also dieses Gleichungssystem auf und löse eine Gleichung davon nach $r$ auf.

$\begin{array}[t]{rll} \text{I} \; 6 - 4r&=&0 &\quad \scriptsize \; \\[5pt] \text{II} \; 2 + 3r &=& 6,5 &\quad \scriptsize \; \\[5pt] \text{III} \; 1 + 2r &=& 4 &\quad \scriptsize \; \\[5pt] \end{array}$

Aus der ersten Gleichung erhältst du $r = \dfrac{6}{4}$ . Setze diesen Wert nun in die anderen Gleichungen ein. Du erhältst wahre Aussagen.

$2+ 3 \cdot \dfrac{6}{4} = 6,5$

$1 + 2 \cdot \dfrac{6}{4} = 4$

Also löst $r = \dfrac{6}{4} = \dfrac{3}{2} = 1,5$ das Gleichungsystem eindeutig und $P$ liegt auf der Geraden $g$ .

3. Schritt: Prüfe, ob $P$ zwischen $A$ und $C$ liegt

Setzt du für den Parameter $r$ $0$ und $1$ in die Geradengleichung ein, erhältst du die Koordinaten der Punkte $A$ und $C$ . Damit $P$ auf der Dreieckseite $\overline{AC}$ liegt, muss für $r$ also gelten

$0 \leq r \leq 1$

Dies ist jedoch für $1,5$ nicht der Fall, da $1,5$ größer als $1$ ist. Also liegt $P$ nicht auf der Dreieckseite $\overline{AC}$ .

2.3

$\blacktriangleright$ Koordinatengleichung aufstellen

Du sollst eine Koordinatengleichung der Ebene $\varepsilon_1$ aufstellen, in der das Dreieck $ABC$ liegt.

Dazu benötigst du zwei Richtungsvektoren und einen Stützvektor der Ebene, in der die Punkte $A$ , $B$ und $C$ liegen. Über das Kreuzprodukt der Richtungsvektoren bestimmst du einen Normalenvektor der Ebene und mithilfe des Stützvektors und des Normalenvektors die Konstante der Koordinatengleichung. Das Kreuzprodukt kannst du allgemein mit folgender Formel ausrechnen

$\overrightarrow{a} \times \overrightarrow{b} = \pmatrix{a_2b_3 - a_3b_2\\a_3b_1 - a_1b_3\\a_1b_2 - a_2b_1}$

Als Richtungsvektoren kannst du zwei beliebige Seitenvektoren des Dreiecks verwenden und als Stützvektor eignet sich der Ortsvektor eines beliebigen Eckpunktes des Dreiecks.

1. Schritt: Normalenvektor bestimmen

Wähle als Richtungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ und berechne den Normalenvektor mithilfe des Kreuzprodukts

$\pmatrix{0\\6\\0} \times \pmatrix{-4\\3\\2} = \pmatrix{6\cdot2 \\ 0 \\ -(6\cdot(-4))} = \pmatrix{12\\0\\24}$

Indem du jede Komponente durch $12$ teilst, erhältst du einen Normalenvektor, mit dem sich die Koordinatenform vereinfacht $\overrightarrow{n} = \pmatrix{1\\0\\2}$ .

2. Schritt: Konstante bestimmen

Die Konstante der Koordinatengleichung bestimmst du mithilfe des Skalarpodukts des Normalenvektors und des Stützvektors der Ebene. Als Stützvektor kannst du $\overrightarrow{OA}$ wählen.

$\overrightarrow{n} \cdot \pmatrix{6\\2\\1} = \pmatrix{1\\0\\2} \cdot \pmatrix{6\\2\\1} = 1 \cdot 6 + 2\cdot 1 = 8$

3. Schritt: Koordinatengleichung aufstellen

Die Koordinatengleichung der Ebene erhältst du mithilfe des Skalaprodukts des Normalenvektors mit einem beliebigen Vektor $\overrightarrow{x} = \pmatrix{x_1\\x_2\\x_3}$ und Gleichsetzen mit der ermittelten Konstante

$\varepsilon_1: \overrightarrow{n} \cdot \overrightarrow{x} = \pmatrix{1\\0\\2} \cdot \pmatrix{x_1\\x_2\\x_3} = x_1 + 2x_3 = 8$

2.4

$\blacktriangleright$ Koordinaten von $\boldsymbol{S‘}$ bestimmen

Gesucht sind die Koordinaten des Punktes $S‘$ , der durch eine Spiegelung des Punktes $S(8 \mid 5 \mid 10)$ an der Ebene $\epsilon_1$ entsteht. Dazu kannst du folgendermaßen vorgehen:

Konstruiere zunächst eine Hilfsgerade senkrecht zur Ebene $\varepsilon_1$ und durch den Punkt $S$ . Bestimme den Schnittpunkt dr Geraden mit der Ebene und verschiebe anschließend den Punkt $S$ , um die Koordinaten des gespiegelten Punktes zu erhalten.

1. Schritt: Konstruiere eine Hilfsgerade

Bestimme zunächst die Gleichung einer Geraden $g$ , die senkrecht zur Ebene $\varepsilon_1$ steht und durch den Punkt $S$ verläuft. Verwende also als Stützvektor $\overrightarrow{OS}$ und als Richtungsvektor einen Normalenvektoren der Ebene, der bereits ermittelt ist.

$g: \overrightarrow{x} = \pmatrix{8\\5\\10} + r \cdot \pmatrix{1\\0\\2}$

2. Schritt: Bestimme den Schnittpunkt der Hilfsgeraden mit der Ebene

Dazu setzt du einen allgemeinen Vektor $\overrightarrow{x}$ der Hilfsgeraden in die Normalenform der Koordinatengleichung von $\varepsilon_1$ ein und löst diese Gleichung nach dem reelen Parameter $r$ auf.

$\begin{array}[t]{rll} 8 + r + 2\cdot (10 + 2r)&=& 8&\quad \scriptsize \mid \text{Vereinfachen} \; \\[5pt] 28 + 5r &=& 8 &\quad \scriptsize \mid -28 \, , \, : 5\; \\[5pt] r &=& - 4 \end{array}$

Indem du diese Lösung in die Geradengleichung einsetzt, erhältst du die Koordinaten des Ortsvektors $\overrightarrow{OM}$ .

$\overrightarrow{OM} = \pmatrix{8\\5\\10} -4\cdot\pmatrix{1\\0\\2} = \pmatrix{4\\5\\2}$

Damit ergeben sich die Koordinaten des Schnittpunktes zu $M(4\mid5\mid2)$ .

3. Schritt: Bestimme die Koordinaten der Spiegelung

Berechne die Koordinaten des Verbindungsvektors $\overrightarrow{SM}$ zwischen dem Schnittpunkt und dem zu spiegelnden Punkt $S$ . Dies entspricht der kürzesten Verbindung zwischen dem Punkt und der Ebene.

$\overrightarrow{SM} = \pmatrix{-4\\0\\-8}$

Um nun die Koordinaten der Spiegelung zu erhalten, musst du $S$ zweimal um diese Strecke verschieben.

Durch die erste Verschiebung gelangst du in die Ebene, durch die zweite Verschiebung gelangst du hinter die Ebene. Somit erhältst du die Koordinaten von $\overrightarrow{OS‘}$

$\overrightarrow{OS‘} = \overrightarrow{OS} + 2\cdot \overrightarrow{SM} = \pmatrix{8\\5\\10} + 2 \cdot \pmatrix{-4\\0\\-8} = \pmatrix{0\\5\\-6}$

Damit ergeben sich die Koordinaten des gespiegelten Punktes zu $S‘(0\mid5\mid-6)$ .

2.5

$\blacktriangleright$ Neigungswinkel berechnen

Du sollst den Neigungswinkel der Seitenfläche $ABS$ gegenüber der Grundfläche der Pyramide berechnen.

Dazu nutzt du, dass du sowohl die Grundfläche der Pyramide als auch die Seitenfläche $ABS$ durch zwei Ebenen $\varepsilon_1$ und $\varepsilon_2$ modellieren kannst. Diese Ebenen schließen einen Schnittwinkel ein, der dem Neigungswinkel von $ABS$ gegenüber der Grundfläche entspricht.

Für diese Ebenen lassen sich Normalenvektoren $\overrightarrow{n_{\varepsilon_1}}$ und $\overrightarrow{n_{\varepsilon_2}}$ berechnen. Diese schließen den Schnittwinkel der beiden Ebenen ein. Für den Winkel zwischen zwei Vektoren gilt allgemein

$\alpha = \mathrm{\arccos}\left(\dfrac{\overrightarrow{n_{\varepsilon_1}}\cdot \overrightarrow{n_{\varepsilon_2}}}{\vert \overrightarrow{n_{\varepsilon_1}} \vert \cdot \vert \overrightarrow{n_{\varepsilon_2}} \vert } \right)$

Der Normalenvektor der Grundflächenebene entspricht dem bereits berechneten Normalenvektor der Ebene des Dreiecks aus Aufgabenteil $\text{2.3}$ . Folglich musst du einen Normalenvektor der Ebene $\varepsilon_2$ finden, in der die Seitenfläche $ABS$ liegt.

Da du hierzu nur zwei Richtungsvektoren benötigst, kannst du $\overrightarrow{AB}$ und $\overrightarrow{AS}$ berechnen.

$\overrightarrow{AB} = \pmatrix{6 - 6\\ 8 - 2\\ 1-1} = \pmatrix{0\\6\\0}$

$\overrightarrow{AS} = \pmatrix{8 - 6\\ 5 - 2\\ 10-1} = \pmatrix{2\\3\\9}$

Berechne nun über das Kreuzprodukt den Normalenvektor

$\overrightarrow{AB} \times \overrightarrow{AS} = \pmatrix{54\\0\\-12}$

Indem du jede Komponente durch $12$ teilst, erhältst du einen Normalenvektor, mit dem sich die Rechnung vereinfacht

$\overrightarrow{n_{\varepsilon_2}} = \pmatrix{4,5\\0\\-1}$

Aus diesem Ergebnis kannst du nun mit $\overrightarrow{n_{\varepsilon_1}} = \pmatrix{1\\0\\2}$ und der obigen Formel direkt den Schnittwinkel berechnen

$\alpha = \mathrm{\arccos}\left( \dfrac{1\cdot 4,5 + 2 \cdot (-1)}{\sqrt{1^2+2^2}\cdot\sqrt{4,5^2+(-1)^2}} \right) \approx \mathrm{\arccos}(0,242) \approx 75,96^{\circ}$

Folglich beträgt der Neigungswinkel der Seitenfläche $ABS$ gegenüber der Grundfläche ungefähr $75,96^{\circ}$ .

2.6

$\blacktriangleright$ Flächeninhalt berechnen

Du sollst den Flächeninhalt der Schnittfläche berechnen, die entsteht, wenn eine zur $xy-$ Ebene parallele und durch den Punkt $C$ verlaufende Ebene $\varepsilon_2$ die Pyramide $ABCS$ schneidet.

Überlege dir zunächst, wie die Ebene verläuft.

Du weißt, dass die Ebene parallel zur $xy-$ Ebene ist. Dadurch werden alle Punkte innerhalb der Ebene bei $z = 3$ liegen, da der Punkt $C$ die $z-$ Koordinate $3$ hat. Demnach kann die Ebene keine anderen Schnittpunkte mit der Grundfläche $ABC$ als $C$ haben, da die $z-$ Koordinaten der Punkte $A$ und $B$ kleiner als $3$ sind.

Dementsprechend muss die Ebene die Pyramide an drei Stellen schneiden: im Punkt $C$ , sowie an zwei Punkten $P_1$ und $P_2$ , die auf den Seiten $\overline{AS}$ und $\overline{BS}$ liegen. Diese Punkte sind somit die Schnittpunkte der Ebene $\varepsilon_2$ mit zwei Geraden $g_1$ und $g_2$ . Dabei geht $g_1$ durch die Punkte $A$ und $S$ und $g_2$ durch die Punkte $B$ und $S$ .

Mit diesen Schnittpunkten ergibt sich ein neues Dreieck $CP_1P_2$ , dessen Flächenhinhalt du mit folgender Formel ausrechnen kannst

$A = \dfrac{\vert \overrightarrow{CP_1} \times \overrightarrow{CP_2} \vert}{2}$

Stelle zuerst die Koordinatenform von $\varepsilon_2$ auf. Da diese Ebene parallel zur $xy-$ Ebene verläuft, kannst du als Normalenvektor den Einheitsvektor in $z-$ Richtung und als Stützvektor $\overrightarrow{OC}$ wählen. Die Umrechnung in Koordinatenform erfolgt analog zu Aufgabenteil $\text{2.3}$ .

$\varepsilon_2: \pmatrix{0\\0\\1} \cdot \pmatrix{x_1\\x_2\\x_3} = x_3 = \pmatrix{0\\0\\1} \cdot \pmatrix{2\\5\\3} = 3$

Stelle als nächstes die Geradengleichung durch $A$ und $S$ und durch $B$ und $S$ auf.

Wähle $\overrightarrow{OA}$ als Stützvektor und $\overrightarrow{AS}$ als Richtungsvektor

$g_1: \overrightarrow{x} = \pmatrix{6\\2\\1} + r \cdot \pmatrix{2\\3\\9}$

Setze nun $\overrightarrow{x}$ in die Koordinatenform von $\varepsilon_1$ ein und löse die Gleichung nach $r$ auf.

$\begin{array}[t]{rll} 1 + 9r&=& 3 &\quad \scriptsize \mid -1 \, :9\; \\[5pt] r&=& \dfrac{2}{9} \end{array}$

Setze diesen Parameter nun in die Gleichung für $g_1$ ein du erhältst den Vektor $\overrightarrow{OP_1}$

$\overrightarrow{OP_1} = \pmatrix{\dfrac{58}{9}\\\dfrac{8}{3}\\3}$

Wähle $\overrightarrow{OB}$ als Stützvektor und $\overrightarrow{BS}$ als Richtungsvektor

$g_2: \overrightarrow{x} = \pmatrix{6\\8\\1} + t \cdot \pmatrix{2\\-3\\9}$

Setze nun $\overrightarrow{x}$ in die Koordinatenform von $\varepsilon_1$ ein und löse die Gleichung nach $t$ auf.

$\begin{array}[t]{rll} 1 + 9t&=& 3 &\quad \scriptsize \mid -3 \, :7\; \\[5pt] t&=& \dfrac{2}{9} \end{array}$

Setze diesen Parameter nun in die Gleichung für $g_2$ ein du erhältst den Vektor $\overrightarrow{OP_2}$

$\overrightarrow{OP_2} = \pmatrix{\dfrac{58}{9}\\\dfrac{22}{3}\\3}$

Berechne nun das Kreuzprodukt

$\begin{array}[t]{rll} \overrightarrow{CP_1} \times \overrightarrow{CP_2}&=& \pmatrix{\frac{40}{9}\\-\frac{7}{3}\\0}\times\pmatrix{\frac{40}{9}\\ \frac{7}{3}\\0} \\[5pt] &=& \pmatrix{0 -0 \\ 0-0\\ \frac{40}{9}\cdot \frac{7}{3}-\left(-\frac{7}{3} \right) \cdot \frac{40}{9}} \\[5pt] &=& \pmatrix{0\\0\\\frac{560}{27}} \\[5pt] \end{array}$

Jetzt kannst du den Flächeninhalt mit der obigen Formel berechnen

$A = \dfrac{\sqrt{0^2 +0^2+ \left(\frac{560}{27} \right)^2}}{2} = \frac{280}{27} \approx 10,37$

Folglich beträgt der Flächeninhalt der Schnittfläche $10,37 \, \text{Flächeneinheiten} =10,37\, \text{FE}$ .

2.7

$\blacktriangleright$ Volumen berechnen

Du sollst das Volumen der Pyramide berechnen. Dazu kannst du folgende Formel verwenden

$V = \dfrac{1}{3} \cdot G \cdot h$

Darin ist $G$ der Inhalt der Grundfläche (in diesem Fall also des Dreiecks $ABC$ ) und $h$ entspricht der Höhe der Pyramide $ABCS$ .

Die Berechnung von $G$ erfolgt mit der Formel für den Flächeninhalt eines Dreiecks aus Aufgabenteil $\text{2.6}$ .

Berechne also $G$ . Wähle zum Beispiel die Seitenvektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ . Ihr Kreuzprodukt ist dir bereits bekannt

$\overrightarrow{AB} \times \overrightarrow{AC} = \pmatrix{12\\0\\-24}$

Daraus ergibt sich $G$ zu

$G = \dfrac{\sqrt{12^2+(-24)^2}}{2} \approx 13, 42$

$h$ entspricht dem Abstand der Spitze der Pyramide (beschrieben durch die Koordinaten des Punktes $S$ ) von der Ebene der Grundfläche. Ihre Gleichung hast du in Koordinatenform vorliegen (vergleiche Aufgabenteil $\text{2.3}$ ).

Den Abstand berechnest du, indem du die Koordinatenform in die Hessesche Normalform bringst und die Koordinaten des Punktes $S$ dort einsetzt. Die Hessesche Normalform berechnest du, indem du die Konstante auf die linke Seite der Koordinatengleichung bringst und durch den Betrag des Normalenvektors teilst.

$\begin{array}[t]{rll} x_1 + 2x_2&=&8 &\quad \scriptsize \mid -8 \, :\sqrt{5}\; \\[5pt] \dfrac{1}{\sqrt{5}} \cdot( x_1 + 2x_2 - 8)&=&0 \end{array}$

Allgemein gilt für den Abstand eines Punktes $P(x_1\mid x_2\mid x_3)$ von der Ebene $\varepsilon_1$

$d(P, \varepsilon_1) = \dfrac{1}{\sqrt{5}} \cdot( x_1 + 2x_2 - 8)$

Setze nun die Koordinaten von $S$ ein und du erhältst

$h \approx 8,94$

Mit $h$ und $G$ ergibt sich das Volumen der Pyramide zu

$V = \dfrac{1}{3} \cdot (G \cdot h) = \dfrac{1}{3} \cdot (13,42 \cdot 8,94) \approx 39,99$

Damit ist das Volumen der Pyramide $39,99 \, \text{VE}$ .

2.8

$\blacktriangleright$ Koordinaten des Punktes $D$ bestimmen

Du sollst die Koordinaten des Punktes $D$ auf der Kante $\overline{SC}$ so bestimmen, dass die Ebene durch $A,B$ und $D$ die Pyramide in zwei volumengleiche Körper teilt.

Das bedeutet, dass durch das Einführen des Punktes $D$ eine zweite Pyramide mit der Grundfläche $ABC$ und der Spitze $D$ entsteht, deren Volumen halb so groß wie das der Pyramide $ABCS$ sein muss.

$\dfrac{1}{2}\cdot V_{ABCS} = V_{ABCD}$

Die Bedingung an den Punkt $D$ ist, dass er auf der Strecke zwischen $C$ und $S$ liegt. Dies bedeutet, dass $D$ auf einer Geraden $g$ liegen muss, die durch diese beiden Punkte verläuft und somit durch eine Geradengleichung mit dem Parameter $r$ beschrieben werden kann.

Stelle also eine allgemeine Formel für das Volumen der Pyramide $ABCD$ auf. In diese kannst du dann einen Ortsvektor $\overrightarrow{x}$ auf der Geraden $g$ einsetzen.

Durch Gleichsetzen mit $\dfrac{1}{2}\cdot V_{ABCS}$ kannst du einen Paramter $r$ bestimmen, der die Position des Punktes $D$ festlegt.

Durch Einsetzen von $r$ in die Geradengleichung erhältst du dann die Koordinaten von $D$ .

Stelle also die Geradengleichung auf. Mit $\overrightarrow{OC}$ als Ortsvektor und $\overrightarrow{CS}$ als Richtungsvektor ergibt sich diese zu

$g: \overrightarrow{x} = \pmatrix{2\\5\\3} + r \cdot \pmatrix{6\\0\\7}$

Nun benötigst du eine allgemeine Formel für das Volumen. Da es sich bei dem betrachteten Körper ebenfalls um eine Pyramide handelt, gilt

$V_{ABCD} = \dfrac{1}{3} \cdot G \cdot h$

Die einzige Unbekannte darin ist $h$ , also der Abstand des Punktes $D$ von der Grundfläche. Mit der Bedingung an das Volumen ergibt sich

$\dfrac{1}{2}\cdot V_{ABCS} = \dfrac{1}{2} \cdot 39,99 = 19,99 = \dfrac{1}{3} \cdot 13,42 \cdot h$

Stelle diese Gleichung nach $h$ um.

$h \approx 4,49$

Du kennst die Formel für $h$ , die sich aus der Hesseschen Normalform ergibt. Setze also in die Hessesche Normalform der Ebene $\varepsilon_1$ die Koordinaten von $\overrightarrow{x}$ auf $g$ ein und forme diese Gleichung nach $r$ um.

$\begin{array}[t]{rll} \dfrac{1}{\sqrt{5}}\cdot(2 + 6r + 2 \cdot (3 + 7r)-8)&=& 4,49&\quad \scriptsize \mid \cdot \sqrt{5} , \text{Vereinfachen}\; \\[5pt] 20r&\approx& 10,03 \quad \scriptsize \mid :20\; \\[5pt] r&\approx& 0,5 \end{array}$

Setze nun $r = 0,5$ in die Geradengleichung ein und du erhältst die Koordinaten von $\overrightarrow{OD}$

$\overrightarrow{OD} = \pmatrix{2\\5\\3} + 0,5 \cdot \pmatrix{6\\0\\7} = \pmatrix{5\\5\\6,5}$

Also hat $D$ die Koordinaten $(5\mid5\mid 6,5)$ .

Bildnachweise [nach oben]

[1]