Wahlteil B1
B1 Analysis
1
Für die Abkühlung von Tee in einer Tasse bei einer konstanten Umgebungstemperatur von  wurde die Temperatur (in
wurde die Temperatur (in  ) in Abhängigkeit von der Zeit
) in Abhängigkeit von der Zeit  (in Minuten) gemessen.
(in Minuten) gemessen.
Der zeitliche Verlauf der Temperatur des Tees kann durch eine Funktion mit der Gleichung
mit der Gleichung
 mit
mit 


 modelliert werden. Der Graph von
modelliert werden. Der Graph von  ist
ist  .
.
Die Messung begann zum Zeitpunkt und ergab eine Temperatur von
und ergab eine Temperatur von  .
.
Nach 5 Minuten wurde eine Temperatur von gemessen.
gemessen.
Der zeitliche Verlauf der Temperatur des Tees kann durch eine Funktion
Die Messung begann zum Zeitpunkt
Nach 5 Minuten wurde eine Temperatur von
1.1
Ermittle die Werte für  und
und  und gib eine Funktionsgleichung an.
und gib eine Funktionsgleichung an.
 Zur Kontrolle:
Zur Kontrolle: 
(3 BE)
1.2
Bestimme die Zeitspanne, in der die Temperatur von  auf
auf  sinkt.
sinkt.
(2 BE)
1.3
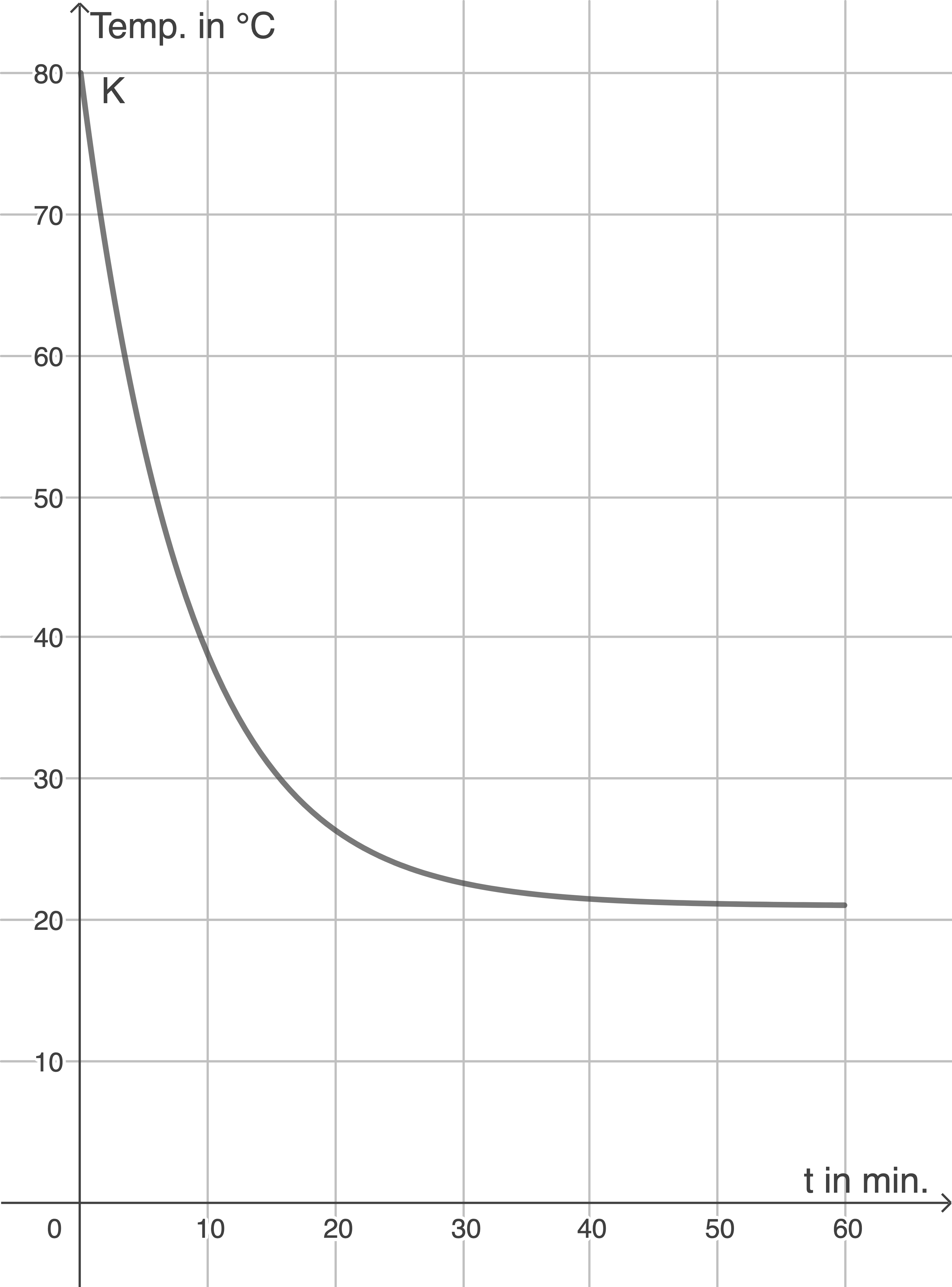
Skizziere  im Intervall
im Intervall  in ein geeignetes Koordinatensystem.
in ein geeignetes Koordinatensystem.
(2 BE)
1.4
Die lokale Änderungsrate von  gibt die Abkühlgeschwindigkeit des Tees in
gibt die Abkühlgeschwindigkeit des Tees in  pro Minute an.
pro Minute an.
1.4.1
Ermittle die Abkühlgeschwindigkeit zum Zeitpunkt 
(2 BE)
1.4.2
Gib den Zeitpunkt an, zu dem der Betrag der Abkühlgeschwindigkeit am größten ist.
Begründe mithilfe der Eigenschaften der Funktion .
.
Begründe mithilfe der Eigenschaften der Funktion
(2 BE)
1.5
Verschiedene Abkühlvorgänge werden durch die Funktionenschar  mit der Gleichung
mit der Gleichung
 mit
mit 

 modelliert.
modelliert.
 ist die Temperatur des Tees zum Zeitpunkt
ist die Temperatur des Tees zum Zeitpunkt  .
.
1.5.1
Beschreibe den Zusammenhang zwischen  und
und  .
.
(2 BE)
1.5.2
Zeige, dass für  die Funktion
die Funktion  auch durch folgende Funktionsgleichung dargestellt werden kann.
auch durch folgende Funktionsgleichung dargestellt werden kann.
 mit
mit  .
.
(2 BE)
1.5.3
Berechne den Wert von  mit
mit  .
.
Interpretiere den Wert von im Sachzusammenhang.
im Sachzusammenhang.
Interpretiere den Wert von
(3 BE)
1.5.4
Betrachtet werden zwei gleichzeitig beginnende Abkühlvorgänge. Der Vorgang  wird modelliert durch die Funktion
wird modelliert durch die Funktion  . Der Vorgang
. Der Vorgang  wird modelliert durch die Funktion
wird modelliert durch die Funktion  .
Berechne den Zeitpunkt
.
Berechne den Zeitpunkt  , ab dem die Temperaturdifferenz beider Tees höchstens
, ab dem die Temperaturdifferenz beider Tees höchstens  beträgt.
beträgt.
(4 BE)
2
Gegeben ist die Funktionenschar  durch die Gleichung
durch die Gleichung
 mit
mit 

 Die Graphen von
Die Graphen von  sind
sind  .
Für jeden Wert von
.
Für jeden Wert von  wird an
wird an  die Tangente
die Tangente  im Punkt
im Punkt  gelegt.
gelegt.
Die Tangente schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  und die
und die  -Achse im Punkt
-Achse im Punkt  .
.
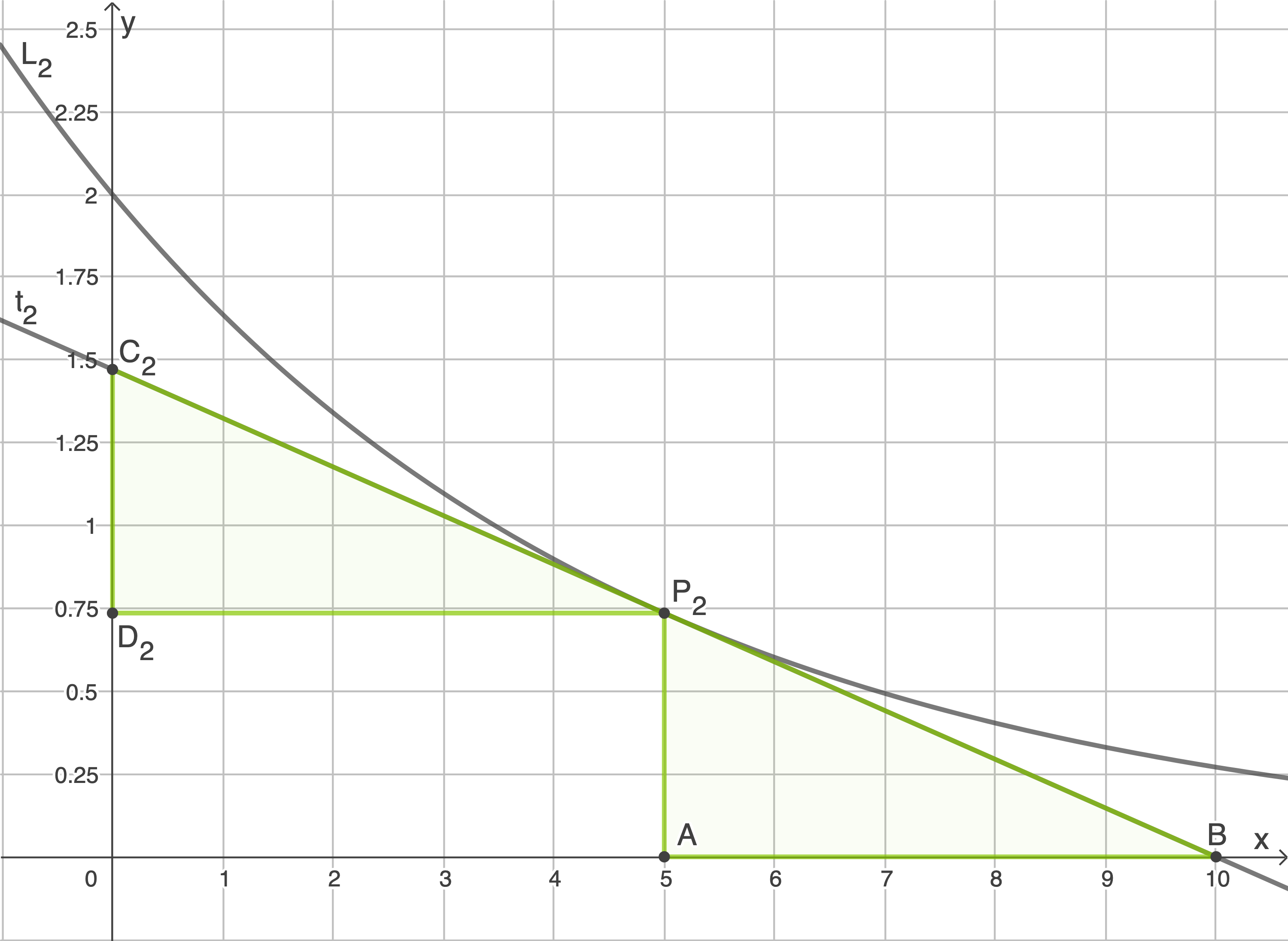
Die Punkte ,
,  , und
, und  bestimmen das Dreieck
bestimmen das Dreieck  .
.
Die Punkte ,
,  und
und  bestimmen das Dreieck
bestimmen das Dreieck  .
Zeige, dass die Flächeninhalte der Dreiecke
.
Zeige, dass die Flächeninhalte der Dreiecke  und
und  gleich groß sind.
gleich groß sind.
Die Tangente
Die Punkte
Die Punkte
(8 BE)
1.1
1.2
1.3
1.4.1
Ableitung




1.4.2
1.5.1
Zum Beispiel:




 Je größer
Je größer  , umso kleiner
, umso kleiner  .
.
1.5.2
1.5.3
1.5.4
2.
Skizze für 
 Nachweis:
Tangentengleichung:
Nachweis:
Tangentengleichung: 


 Setze ein:
Setze ein:
![\(\begin{array}[t]{rll}
\dfrac{a}{\mathrm{e}}&=&- \dfrac {a}{5\mathrm{e}} \cdot 5 + n_a &\quad \scriptsize \mid\;+\frac{5a}{5e} \\[5pt]
\dfrac{2a}{e} &=& n_a&\quad \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/af72bc52e15f4651ff196da8b3a0eee7176376b0bf8a840b66fb71a8a96e1c59_light.svg)
 Berechne die Nullstellen von
Berechne die Nullstellen von 
![\(\begin{array}[t]{rll}
- \dfrac {a}{5\mathrm{e}} \cdot x + \dfrac{2a}{\mathrm{e}}&=&0 &\quad \scriptsize \mid\;-\frac{2a}{\mathrm{e}} \\[5pt]
- \dfrac {a}{5\mathrm{e}} \cdot x &=& -\dfrac{2a}{\mathrm{e}}&\quad \scriptsize \mid\;:\left(- \frac {a}{5\mathrm{e}}\right) \\[5pt]
x&=&10 &\quad \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0e0b312d40f81b7092ef720fe8f606194be06cea144f6860cdf2eaec2af217be_light.svg) Die beiden Dreiecke sind nach Vorgabe der Lage der Punkte rechtwinklig.
Die beiden Dreiecke sind nach Vorgabe der Lage der Punkte rechtwinklig.
Die Länge der Kathteten und
und  ist konstant gleich
ist konstant gleich  .
.
Da der Anstieg der Tangenten konstant ist, sind die Längen der Strecken und
und  gleich. Die beiden Dreiecke sind nach dem Kongruenzsatz SWS kongruent, also auch flächengleich.
Alternativ: Berechnung der Flächeninhalte in Abhängigkeit von
gleich. Die beiden Dreiecke sind nach dem Kongruenzsatz SWS kongruent, also auch flächengleich.
Alternativ: Berechnung der Flächeninhalte in Abhängigkeit von  Dreieck
Dreieck 
 Dreieck
Dreieck 



Die Länge der Kathteten
Da der Anstieg der Tangenten konstant ist, sind die Längen der Strecken