3 Analytische Geometrie – Wahlaufgabe

Ein Spielturm auf einem Spielplatz hat die Form eines geraden Prismas mit einem aufgesetzten Dach in Form einer geraden Pyramide. Die Bodenfläche des Spielturms wird durch das regelmäßige Sechseck $ABCDEF$ mit der Seitenlänge $80\;\text{cm},$ die Grundfläche des Dachs durch das regelmäßige Sechseck $GHIJKL$ mit der Seitenlänge $1\;\text{m}$ modellhaft beschrieben. Gegeben sind die Koordinaten folgender Punkte:

$A(x\mid4\mid 0), B(0\mid8\mid 0), F(x\mid-4\mid 0),$ $G(5 \sqrt{3}\mid5\mid 15), H(0\mid10\mid 15)$ und $L(5 \sqrt{3}\mid-5\mid 15).$
Der Punkt $S(0\mid0\mid 25)$ stellt im Modell die Dachspitze dar.

Die $xy$ -Ebene beschreibt den horizontalen Untergrund, eine Längeneinheit im Koordinatensystem entspricht $10\;\text{cm}$ in der Wirklichkeit. Abbildung 1 zeigt ein Foto des Spielturms, Abbildung 2 die Grundfläche des Prismas und die Projektion der Grundfläche der Pyramide in die $xy$ -Ebene.

Holzspielhaus im Garten mit Satteldach und Fenster, umgeben von grünem Gras und Bäumen.

Abbildung 1

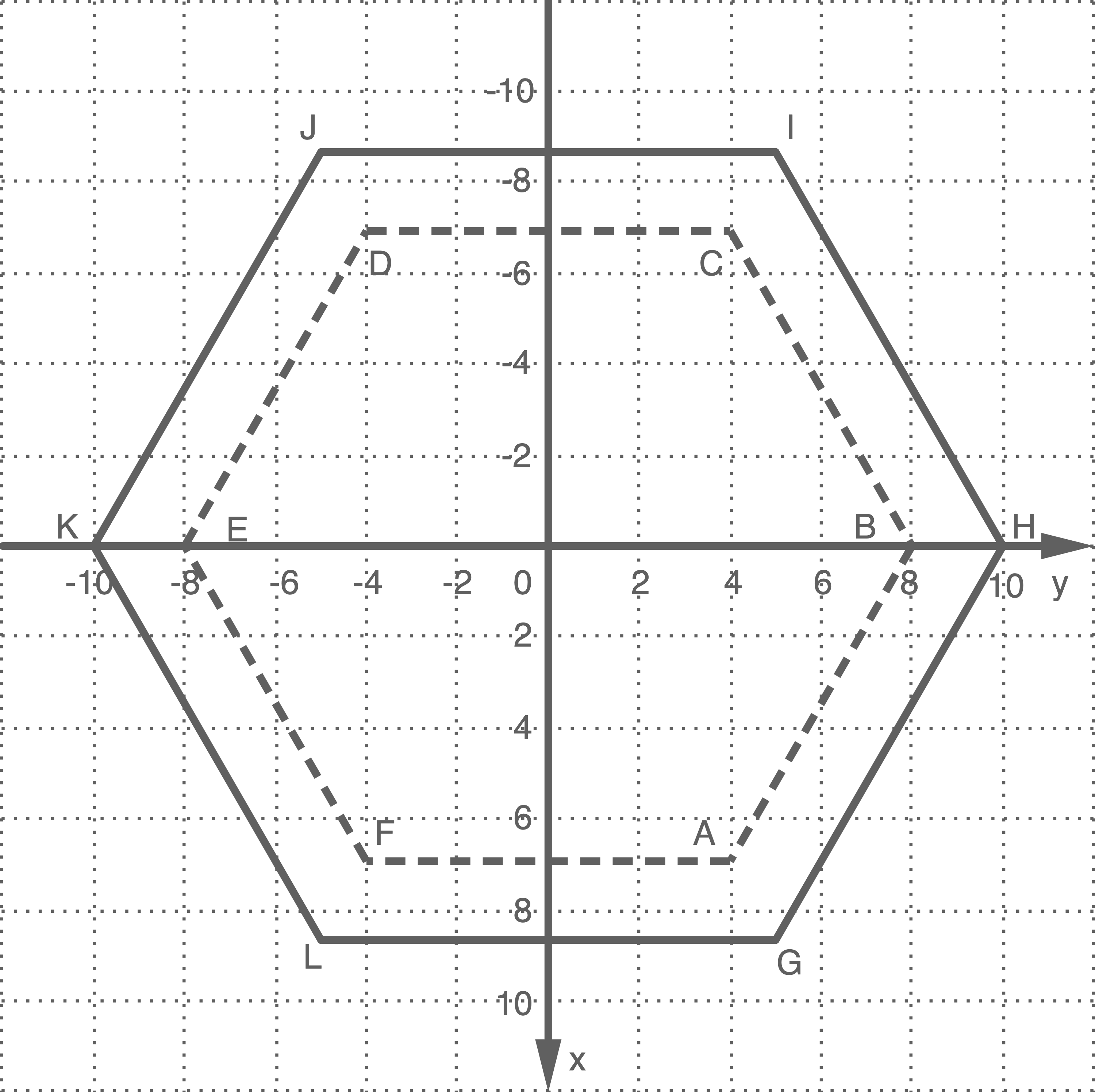
Diagramm eines Sechsecks im Koordinatensystem mit Linien und Punkten.

Abbildung 2

3.1

Das Dach des Spielturms wird von sechs schräg verlaufenden Balken getragen, die zur Dachspitze führen. Im Modell wird ein solcher Balken als Strecke zwischen einem Eckpunkt der Fläche $GHIJKL$ und dem Punkt $S$ dargestellt.

Berechne die Länge eines der Balken in Meter.

(2 BE)

3.2

Das Dach des Spielturms soll renoviert werden. Es entspricht im Modell der Mantelfläche der Pyramide. Berechne dazu die Größe der Dachfläche.

(3 BE)

3.3

Die Eckpunkte $A$ und $F$ haben die gleiche $x$ -Koordinate. Zeige, dass diese den Wert $4 \cdot \sqrt{3}$ hat.

(3 BE)

3.4

Das Modell des Spielturms besitzt mehrere Symmetrieebenen. Eine der Symmetrieebenen wird durch die Gleichung $x+\sqrt{3} \cdot y=0$ beschrieben. Zeichne in der Abbildung 2 diese Ebene als senkrechte Projektion in die $xy$ -Ebene ein.

(1 BE)

3.5

Im Dach des Spielturms befindet sich ein Loch. Dieses kann modellhaft durch den Punkt $P(\sqrt{3}\mid0\mid 23)$ dargestellt werden. Der Punkt $P$ liegt im Dreieck $SLG.$

Ein Lichtstrahl trifft durch dieses Loch und verläuft geradlinig ins Innere des Spielturms. Dort erzeugt er einen Lichtpunkt auf einer der Innenflächen. Dieser Lichtpunkt wird im Modell mit $Q$ bezeichnet. Für einen Zeitraum beschreibt die Gleichung $\overrightarrow{x}=\pmatrix{\sqrt{3}\\0\\23}+r \cdot\pmatrix{-1\\0\\-k}$ mit $r, k \in \mathbb{R}, k\gt0$ den sich ändernden Verlauf des Lichtstrahls in Abhängigkeit von $k.$

3.5.1

Für $k=\dfrac{23}{15} \sqrt{3}$ liegt $Q$ im Mittelpunkt der Strecke $\overline{DC}.$ Berechne dafür die Größe des Winkels, den der Lichtstrahl mit dem horizontalen Untergrund bildet.

(3 BE)

3.5.2

Begründe ohne Rechnung, dass der Lichtstrahl für $k=\dfrac{25}{15} \sqrt{3}$ auf dem Boden des Spielturms zu sehen ist.

(2 BE)

3.6

Auf die Dachspitze des Spielturms ist ein $50\;\text{cm}$ hoher Mast aufgesetzt, der senkrecht zum Untergrund steht. Ein Kind steht zunächst neben dem Spielturm und blickt aus einer Augenhöhe von einem Meter in Richtung Mastspitze. Anschließend bewegt es sich rückwärtsgehend vom Spielturm weg, bis es die Mastspitze sehen kann.

Im Modell wird die Position des Kindes auf dem horizontalen Untergrund durch den Punkt $(8\mid2\mid 0)$ beschrieben und seine Bewegungsrichtung durch den Vektor $\pmatrix{1\\0\\0}.$

Ermittle, bis zu welcher Position das Kind mindestens gehen muss, um die Mastspitze sehen zu können.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

$\begin{array}[t]{rlll} \left\vert\overrightarrow{SH}\right\vert&=&\left\vert\pmatrix{0-0\\10-0\\15-25}\right\vert \\[5pt] &=&\sqrt{0^2+10^2+(-10)^2} \\[5pt] &=&10\sqrt{2} \end{array}$

Die Länge eines Balkens beträgt somit $0,1\cdot10\sqrt{2}\approx1,41\;\text{m}.$

3.2

Aus den Koordinaten von $G$ und $H$ folgt $M(2,5\sqrt{3}\mid7,5\mid15)$ für die Koordinaten des Mittelpunkts der Kante $\overline{GH}.$ Für die Höhe der Seitenflächen der Pyramide folgt somit:

$\begin{array}[t]{rlll} \left\vert\overrightarrow{SM}\right\vert&=&\left\vert\pmatrix{2,5\sqrt{3}-0\\7,5-0\\15-25}\right\vert \\[5pt] &=&\sqrt{\left(2,5\sqrt{3}\right)^2+7,5^2+(-10)^2} \\[5pt] &=&\sqrt{175} \end{array}$

Für die Länge der Grundseite $\overline{GH}$ gilt:

$\begin{array}[t]{rlll} \left\vert\overrightarrow{GH}\right\vert&=&\left\vert\pmatrix{0-5\sqrt{3}\\10-5\\15-15}\right\vert \\[5pt] &=&\sqrt{\left(-5\sqrt{3}\right)^2+5^2} \\[5pt] &=&10 \end{array}$

Insgesamt ergibt sich damit für die Größe $A$ der Dachfläche:

$\begin{array}[t]{rlll} A&=&6\cdot\dfrac{1}{2}\cdot\left\vert\overrightarrow{GH}\right\vert\cdot\left\vert\overrightarrow{SM}\right\vert \\[5pt] &=&6\cdot\dfrac{1}{2}\cdot10\cdot\sqrt{175} \\[5pt] &\approx&397\;[\text{cm}^2] \end{array}$

3.3

Der Abstand aller Eckpunkte des Daches zu $S$ ist gleichgroß. Da $S$ über dem Koordinatenursprung liegt, ist auch der Abstand aller Eckpunkte zu diesem gleich. Damit ergibt sich für $x:$

$\begin{array}[t]{rlll} \left\vert\overrightarrow{OA}\right\vert&=&\left\vert\overrightarrow{OB}\right\vert \\[5pt] \left\vert\pmatrix{x\\4\\0}\right\vert&=&\left\vert\pmatrix{0\\8\\0}\right\vert \\[5pt] \sqrt{x^2+4^2}&=&\sqrt{8^2} &\mid\;^2\\[5pt] x^2+16&=&64 &\mid\;-16\\[5pt] x^2&=&48 &\mid\;\sqrt{\;}\\[5pt] x_{1;2}&=&\pm4\sqrt{3} \end{array}$

Da aus dem Grundriss hervorgeht, dass $A$ und $F$ eine positive $x$ -Koordinate besitzen, folgt $x=4\sqrt{3}.$

3.4

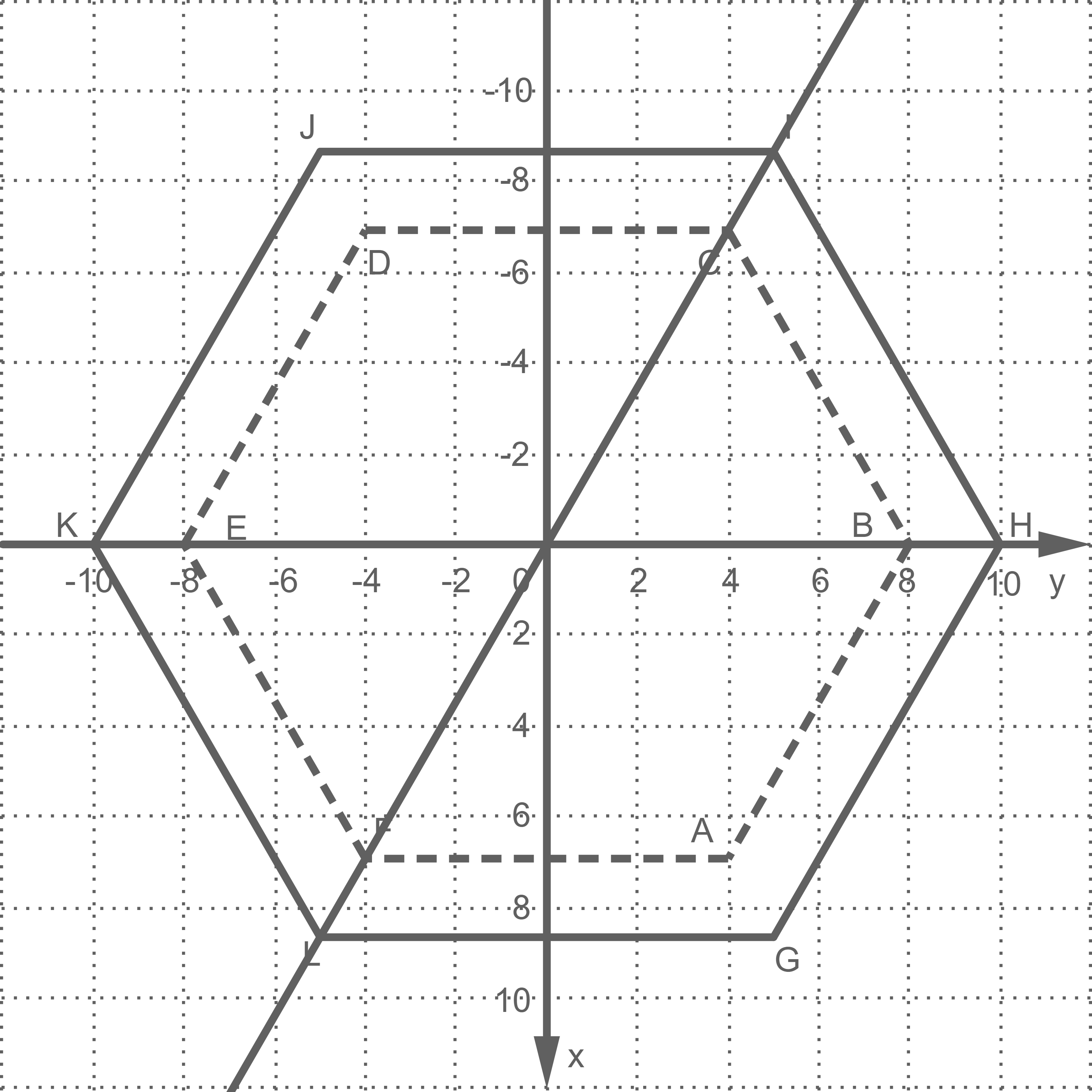
Grafik eines Koordinatensystems mit einem polygonalen Diagramm und markierten Punkten.

3.5

3.5.1

Ein Normalenvektor der $xy$ -Ebene ist durch $\overrightarrow{n}=\pmatrix{0\\0\\1}$ gegeben. Damit folgt für den gesuchten Winkel:

$\begin{array}[t]{rlll} \cos(\alpha)&=&\dfrac{\left\vert\pmatrix{-1\\0\\-\frac{23}{15}\sqrt{3}}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{-1\\0\\-\frac{23}{15}\sqrt{3}}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert} \\[5pt] \cos(\alpha)&=&\dfrac{\frac{23}{15}\sqrt{3}}{\sqrt{(-1)^2+\left(-\frac{23}{15}\sqrt{3}\right)^2}\cdot\sqrt{1}} \\[5pt] \cos(\alpha)&=&\dfrac{\frac{23}{15}\sqrt{3}}{\sqrt{1+\left(-\frac{23}{15}\sqrt{3}\right)^2}} \\[5pt] \alpha&=&\cos^{-1}\left(\dfrac{\frac{23}{15}\sqrt{3}}{\sqrt{1+\left(-\frac{23}{15}\sqrt{3}\right)^2}}\right) \\[5pt] \alpha&\approx&20,6^\circ \end{array}$

3.5.2

Die Veränderung der Koordinaten des Lichtpunktes in $z$ -Richtung wird durch $r\cdot(-k)$ beschrieben. Da $\frac{25}{15}\sqrt{3}\gt\frac{23}{15}\sqrt{3}$ gilt, verläuft der Lichtstrahl steiler als in Teilaufgabe 3.5.1 und ist somit auf dem Boden des Spielturms zu sehen.

3.6

Eine Längeneinheit entspricht $10\;\text{cm}$ bzw. $0,1\;\text{m}.$ Damit ergibt sich $(0\mid0\mid30)$ für die Koordinaten der Mastspitze. Für den Ortsvektor des Punktes $A_K,$ an dem die Augen des Kindes sich befinden gilt:

$\overrightarrow{OA_K}=\pmatrix{8+r\\2+0\\10+0}$

Da das Kind anfangs unterhalb der Kante $\overline{LG}$ steht und sich nach außen wegbewegt, ist der Punkt gesucht, an dem die Ebene $LGA_K$ die Mastspitze enthält. Für die Ebenengleichung dieser Ebene ergibt sich:

Ebenengleichung anzeigen

Gleichsetzen der Ebenengleichung mit der Mastspitze liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&5\sqrt{3}+t\cdot(8+r-5\sqrt{3})&=& 0 \\ \text{II}\quad&-5+10s+7t&=&0 \\ \text{III}\quad&15-5t&=&30 \end{array}$

Gleichung $\text{III}$ liefert direkt $t=-3.$ Einsetzen in Gleichung $\text{II}$ ergibt weiter:

$\begin{array}[t]{rlll} -5+10s+7\cdot(-3)&=&0 &\mid\;+26 \\[5pt] 10s&=&26 &\mid\;:10 \\[5pt] s&=&2,6 \end{array}$

Einsetzen von $t=-3$ in Gleichung $\text{I}$ liefert außerdem:

$\begin{array}[t]{rlll} 5\sqrt{3}+(-3)\cdot(8+r-5\sqrt{3})&=&0 &\mid\;+3r \\[5pt] 20\sqrt{3}-24&=&3r &\mid\;:3 \\[5pt] 3,5&\approx&r \end{array}$

Einsetzen von $r$ in die Koordinaten für die Augen des Kindes liefert somit, dass das Kind mindestens zur ungefähren Position $(11,5\mid2\mid0)$ gehen muss, um die Mastspitze zu sehen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?