1 Analysis – Pflichtaufgabe

1.1

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ durch die Gleichung $f_a(x)=\frac{1}{a} x^3-2 x^2+a \cdot x$ mit $a \in \mathbb{R}, a\gt0.$

1.1.1

Berechne die Nullstellen von $f_3$ und den Wert der ersten Ableitung von $f_3$ an der Stelle $3.$

(4 BE)

1.1.2

Für jeden Wert von $a$ sind $\left(x_1 \mid f_a\left(x_1\right)\right)$ und $\left(x_2 \mid 0\right)$ Punkte des Graphen.

Begründe, dass folgende Aussage wahr ist:

Bezeichnet man die Ableitungsfunktion von $f_a$ mit $\(f_a$ so gilt:

$\(\displaystyle\int_0^{x_1} f_a$

(3 BE)

1.1.3

Gegeben ist die Funktion $g$ mit der Gleichung $g(x)=-f_3(x-2)+1.$

Beschreibe, wie der Graph von $g$ aus dem Graphen von $f_3$ hervorgeht.

(3 BE)

1.2

In einem Labor werden Werkstücke verschiedenen Lebensdauerprüfungen unterzogen. Dazu wird auf ein Werkstück eine sich ändernde Kraft ausgeübt. Die Änderungsrate dieser Kraft wird in Abhängigkeit von der Zeit mithilfe der in $\mathbb{R}$ definierten Funktion $r$ mit der Gleichung $r(x)=x^2-4 x+3$ modellhaft beschrieben.
Dabei ist $r(x)$ die Änderungsrate der Kraft in $\frac{\text{N}}{\text{s}}$ (Newton pro Sekunde) und $x$ die Zeit in $s$ (Sekunden). Die Wirkung der Kraft wird im Zeitraum von $0 \leq x \leq 4$ betrachtet. Zum Zeitpunkt $0 \;\text{s}$ wirkt keine Kraft auf das Werkstück. In Abbildung 1 ist der Graph der Funktion $r$ dargestellt. Die Funktion $r$ entspricht der ersten Ableitungsfunktion von $f_3.$

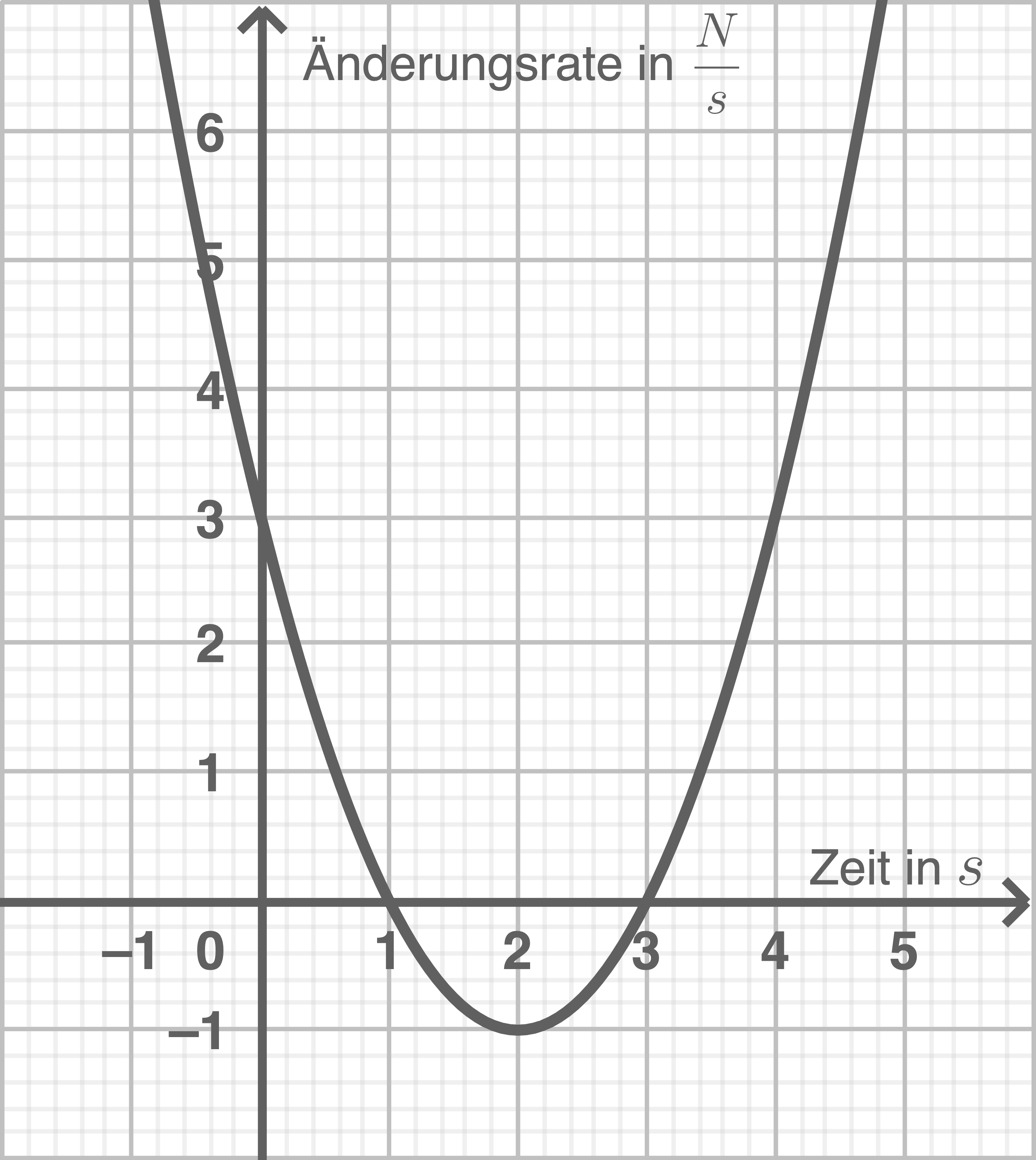
Graph einer Funktion mit Änderung in N/s über Zeit in Sekunden.

Abbildung 1

1.2.1

Gib mithilfe der Abbildung 1 den Zeitraum an, zu dem die Änderungsrate der Kraft höchstens $1 \; \frac{\text{N}}{\text{s}}$ beträgt.

(2 BE)

1.2.2

Berechne die Kraft, die $1\;\text{s}$ nach Beobachtungsbeginn auf das Werkstück wirkt.

(3 BE)

1.2.3

Zum Zeitpunkt $0\;\text{s}$ wirkt nun eine bestimmte Kraft auf das Werkstück ein.

Beurteile, ob die folgende Aussage stets wahr ist, und veranschauliche deine Überlegungen in der Abbildung 1.

Der Betrag der Kraft ist $1\;\text{s}$ nach Beobachtungsbeginn gleich dem Betrag der Kraft, die $4\;\text{s}$ nach Beobachtungsbeginn auf das Werkstück ausgeübt wird.

(4 BE)

1.3

Bei einer anderen Lebensdauerprüfung wird das Werkstück periodisch Zug- und Druckkräften ausgesetzt. Die zu einem Zeitpunkt wirkende Kraft wird mithilfe der reellen Funktion $w$ mit $w(x)=-3 \cdot \sin \left(\dfrac{\pi}{2} \cdot x\right)$ beschrieben. Dabei ist $w(x)$ die Kraft in $\text{N}$ (Newton) und $x$ die Zeit in $\text{s}$ (Sekunden). Die Abbildung 2 zeigt für einen Beobachtungszeitraum von $0$ bis $6$ Sekunden den Graphen von $w.$

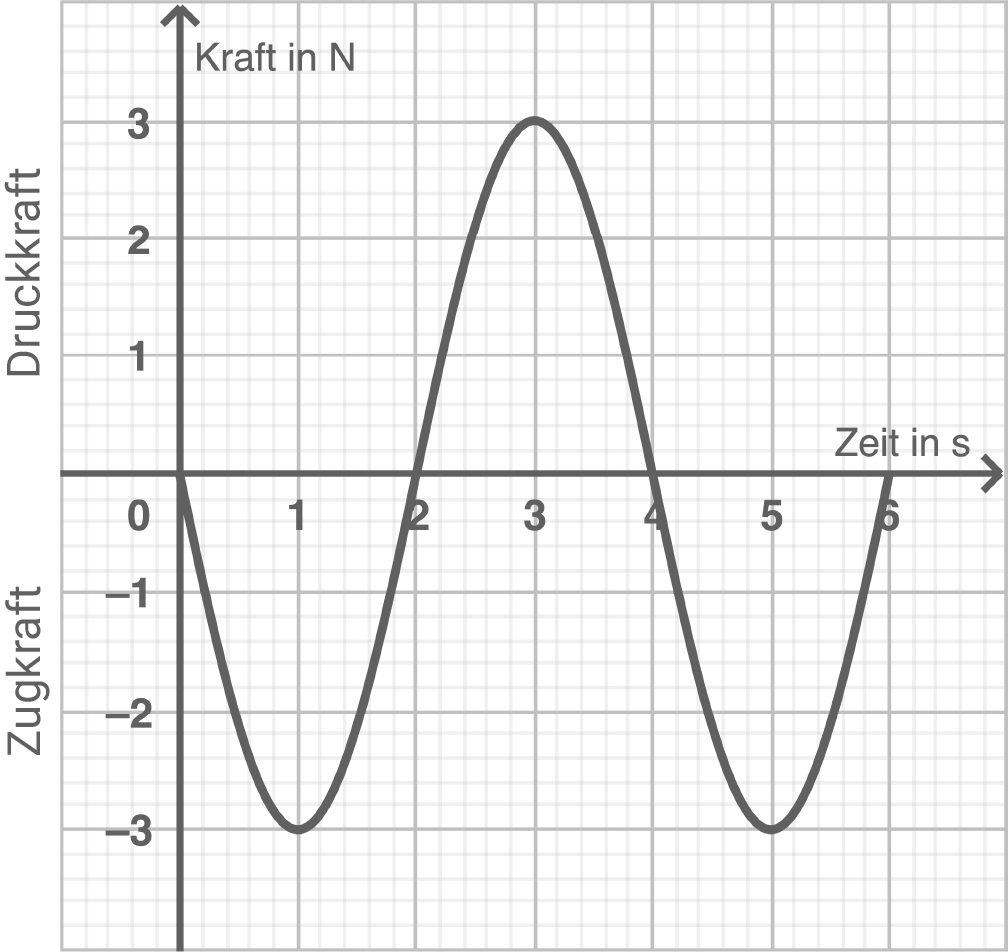
Graph mit Druck- und Zugkraft über die Zeit, dargestellt in Newton und Sekunden.

Abbildung 2

1.3.1

Ermittle graphisch die Kraft, die zum Zeitpunkt $2,5\;\text{s}$ auf das Werkstück wirkt.

(1 BE)

1.3.2

Berechne den Zeitpunkt, zu dem zum zweiten Mal nach Beobachtungsbeginn eine Druckkraft von $1\;\text{N}$ auf das Werkstück wirkt.

(3 BE)

1.3.3

Mit dem Term $\dfrac{1}{b-a} \cdot \displaystyle\int_a^b w(x) \;\text{d} x$ kann die durchschnittlich wirkende Kraft im Zeitintervall $[a ; b]$ bestimmt werden.

Berechne diese für die ersten zwei Sekunden ab Beobachtungsbeginn.

(3 BE)

1.3.4

Das Prüfverfahren soll nun so verändert werden, dass folgende Vorgaben erfüllt sind:

Druck- und Zugkräfte wechseln weiterhin periodisch.
Der maximale Betrag der Druck- bzw. der Zugkraft ist $4\;\text{N}.$
Zum Zeitpunkt $0\;\text{s}$ ist die Änderungsrate der wirkenden Kraft maximal.
Zum Zeitpunkt $3\;\text{s}$ wirkt die maximale Druckkraft zum zweiten Mal.

Ermittle für das veränderte Prüfverfahren die Gleichung einer Sinusfunktion $v,$ welche die zu einem Zeitpunkt $x$ wirkende Kraft beschreibt.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

1.1.1

Nullstellen berechnen

$\begin{array}[t]{rlll} f_3(x)&=&0 \\[5pt] \dfrac{1}{3}x^3-2x^2+3x&=&0 \\[5pt] x\cdot\left(\dfrac{1}{3}x^2-2x+3\right)&=&0 \end{array}$

Mit dem Satz des Nullprodukts folgt $x_1=0$ und weiter mit der $abc$ -Formel:

$\begin{array}[t]{rlll} x_{2;3}&=&\dfrac{2\pm\sqrt{(-2)^2-4}}{\frac{2}{3}} \\[5pt] &=&\dfrac{2\pm0}{\frac{2}{3}} \\[5pt] &=&3 \end{array}$

Die Nullstellen von $f_3$ sind somit $x_1=0$ und $x_2=3.$

Wert der Ableitung berechnen

Für die erste Ableitung von $f_3$ gilt:

$\(f_3$

An der Stelle $x=3$ gilt somit:

$\(\begin{array}[t]{rlll} f_3$

1.1.2

Da $f_a$ eine Stammfunktion von $\(f_a$ ist, gilt:

$\(\begin{array}[t]{rlll} \displaystyle\int_0^{x_1} f_a$

$\(\begin{array}[t]{rlll} -\displaystyle\int_{x_1}^{x_2} f_a$

Damit ist die Aussage aus der Aufgabenstellung wahr.

1.1.3

Der Graph von $g$ geht durch Verschiebung um zwei Einheiten in $x$ -Richtung, anschließende Spiegelung an der $x$ -Achse und Verschiebung um eine Einheit in $y$ -Richtung aus dem Graphen von $f_3$ hervor.

1.2

1.2.1

In dem Zeitraum zwischen $0,6\;\text{s}$ und $3,4\;\text{s}$ beträgt die Änderungsrate der Kraft höchstens $1\;\frac{\text{N}}{\text{s}}.$

1.2.2

$\begin{array}[t]{rlll} \displaystyle\int_{0}^{1}r(x)\;\mathrm dx&=&\displaystyle\int_{0}^{1}x^2-4x+3\;\mathrm dx \\[5pt] &=&\left[\dfrac{1}{3}x^3-2x^2+3x\right]_0^1 \\[5pt] &=&\dfrac{1}{3}\cdot1^3-2\cdot1^2+3\cdot1-0 \\[5pt] &=&\dfrac{4}{3}\;[\text{N}] \end{array}$

1.2.3

Aussage beurteilen

$\begin{array}[t]{rlll} \displaystyle\int_{0}^{4}r(x)\;\mathrm dx&=&\displaystyle\int_{0}^{4}x^2-4x+3\;\mathrm dx \\[5pt] &=&\left[\dfrac{1}{3}x^3-2x^2+3x\right]_0^4 \\[5pt] &=&\dfrac{1}{3}\cdot4^3-2\cdot4^2+3\cdot4-0 \\[5pt] &=&\dfrac{4}{3}\;[\text{N}] \end{array}$

Da diese Kraft gleich der aus Teilaufgabe 1.2.2 ist, stimmt die Aussage.

Überlegungen veranschaulichen

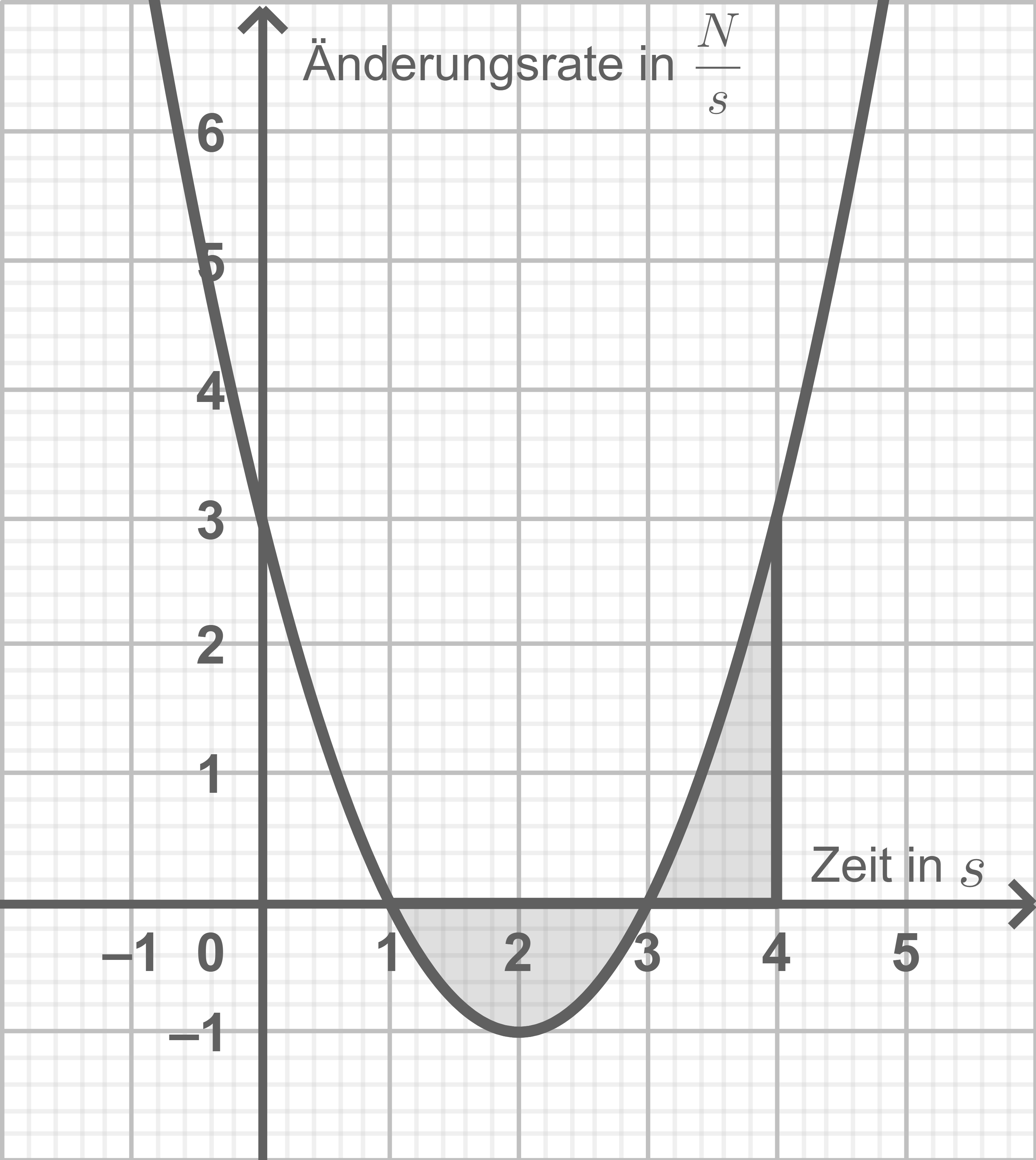
Diagramm einer Funktion mit Änderung in der Zeit, dargestellt in einem Koordinatensystem.

Der Anteil der markierten Fläche, der unterhalb der $x$ -Achse liegt ist genauso groß wie der Anteil, der überhalb der $x$ -Achse liegt, wodurch sich die beiden Flächen aufheben und somit die Kraft $4\;\text{s}$ nach Beobachtungsbeginn der $1\;\text{s}$ nach Beobachtungsbeginn entspricht.

1.3

1.3.1

In der Abbildung lässt sich erkennen, dass $w(2,5)\approx2,1$ gilt und somit die Kraft nach $2,5\;\text{s}$ ungefähr $2,1\;\text{N}$ beträgt.

1.3.2

$\begin{array}[t]{rlll} w(x)&=&1 \\[5pt] -3\cdot\sin\left(\dfrac{\pi}{2}x\right)&=&1 &\mid\;:(-3) \\[5pt] \sin\left(\dfrac{\pi}{2}x\right)&=&-\dfrac{1}{3} &\mid\;\sin^{-1} \\[5pt] \dfrac{\pi}{2}x&=&\sin^{-1}\left(-\dfrac{1}{3}\right) &\mid\;\cdot\dfrac{2}{\pi} \\[5pt] x&\approx&-0,22 \end{array}$

Die Periodenlänge von $w$ ist $4,$ somit ergibt $4-0,22=3,78$ einen anderen Zeitpunkt, zu dem die Druckkraft $1\;\text{N}$ beträgt. Mit Hilfe der Abbildung lässt sich erkennen, dass das der gesuchte Zeitpunkt ist.

1.3.3

Rechenweg anzeigen

$\dfrac{1}{2-0}\cdot\displaystyle\int_{0}^{2}w(x)\;\mathrm dx \approx -1,91$

Die durchschnittlich wirkende Kraft im betrachteten Zeitraum beträgt somit ca. $1,91\;\text{N}.$

1.3.4

Die einzelnen Bedingungen liefern die Parameter der allgemeinen Sinusfunktion $v(x)=a\cdot\sin(bx+c)+d.$ Da die Änderungsrate der Kraft laut 3. bei $x=0$ maximal sein soll, folgt $a\gt0, c=0$ und $d=0.$ Laut 2. soll die Amplitude zusätzlich $4\;\text{N}$ betragen, sodass zusammen $a=4$ folgt. Die vierte Aussage liefert, dass das zweite Maximum der Sinusfunktion bei $x=3$ liegen soll. Da das zweite Maximum nach $1,25$ Periodenlängen auftritt, folgt damit für $b:$

$\begin{array}[t]{rlll} 1,25\cdot\dfrac{2\pi}{b}&=&3 &\mid\;\cdot b \\[5pt] 2,5\pi&=&3b &\mid\;:3 \\[5pt] \dfrac{5}{6}\pi&=&b \end{array}$

Damit ergibt sich insgesamt $v(x)=4\cdot\sin\left(\dfrac{5\pi}{6} x\right).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?