Wahlteil B2

Analytische Geometrie

In einem kartesischen Koordinatensystem wird ein Spat $ABCDEFGH$ betrachtet. Gegeben sind die Koordinaten der Eckpunkte $A(6 \mid 2 \mid 0)$ , $B(5 \mid 5 \mid1)$ , $C(1\mid5\mid1)$ , $E(4 \mid 0 \mid 6)$ , $F(3\mid3\mid7)$ und $H(0 \mid 0 \mid 6)$ .

2.1

Ermittle die Koordinaten der Punkte $D$ und $G$ .
Zeichne den Körper in ein kartesisches Koordinatensystem.

2.2

Berechne das Volumen des Spates.

2.3

Die Gerade $g$ mit der Gleichung

$\overrightarrow{x}=\pmatrix{3 \\ -1 \\ 4}+t\pmatrix{-1 \\ 3 \\ 1}$ ; $t\in\mathbb{R}$

durchstößt die Seitenfläche $ADHE$ und $BCGF$ .

Zeige, dass der Punkt $P(\dfrac{7}{4}\mid \dfrac{11}{4}\mid \dfrac{21}{4})$ auf $g$ und innerhalb des Spates liegt.

2.4

Berechne den Abstand der Kante $\overline{AE}$ zur Kante $\overline{BF}$ .

(zur Kontrolle: Abstand: $\dfrac{2}{11} \sqrt{330}$ )

2.5

Für jeden Wert von $a\, (a\in\mathbb{R}, 1\lt a\lt 6)$ schneidet die Ebene mit der Gleichung $z=a$ die Kante $\overline{AE}$ im Punkt $R_a$ und die Kante $\overline{BF}$ im Punkt $S_a$ .

Berechne den Wert von $a$ so, dass der Inhalt der Fläche $ABS_aR_a\;$ $A=\dfrac{7}{3}\sqrt{30}$ ist.

(30P)

2.1

$\blacktriangleright$ Koordinaten fehlender Eckpunkte berechnen

Bei dieser Aufgabe sollst du die Koordinaten der fehlenden Eckpunkte $D$ und $G$ des Spates berechnen. Da bei einem Spat gegenüberliegende Flächen deckungsgleich sind, kannst du den Vektor $\overrightarrow{EH}$ auf den Ortsvektor $\overrightarrow{OA}$ addieren, um die Koordinaten für Punkt $D$ zu erhalten. Analog verfährst du für die Koordinaten des Punktes $G$ .

Tipp
Das geometrische Objekt Spat hat die Besonderheit, dass gegenüberliegende Flächen deckungsgleich und parallel zueinander sind. Zusätzlich sind alle Flächen Parallelogramme.

$\begin{array}[t]{rll} \overrightarrow{OD}&=& \overrightarrow{OA}+\overrightarrow{EH}\\[5pt] &=&\pmatrix{6 \\ 2 \\ 0}+\pmatrix{-4 \\ 0 \\ 0} \\[5pt] &=& \pmatrix{2 \\ 2 \\ 0} \end{array}$

Somit lauten die Koordinaten für den Punkt $D(2\mid2\mid0)$ . Analog verfährst du nun für Punkt $G$ . Hier addierst du den Vektor $\overrightarrow{BC}$ auf den Ortsvektor $\overrightarrow{OF}$ .

$\begin{array}[t]{rll} \overrightarrow{OG}&=&\overrightarrow{OF}+\overrightarrow{BC} \\[5pt] &=&\pmatrix{3 \\ 3 \\ 7}+\pmatrix{-4 \\ 0 \\ 0} \\[5pt] &=&\pmatrix{-1 \\ 3 \\ 7} \end{array}$

Die Koordinaten für den Punkt $G$ lauten folglich $G(-1\mid3\mid7)$ .

$\blacktriangleright$ Körper in Koordinatensystem einzeichnen

Nun sollst du den Körper noch in ein kartesisches Koordinatensystem einzeichnen. Schau dir zuerst die Koordinaten der Punkte an, um ein Gefühl für die Achsenlängen zu bekommen. Anschließend zeichnest du die Punkte ins Koordinatensystem und zeichnest dann den Spat. Dies sieht wie folgt aus:

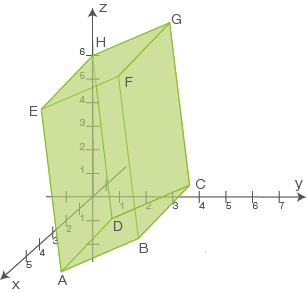3D-Diagramm eines Quaders im Raum mit Achsenbeschriftungen.

Abb. 1: Spat im kartesischen Koordinatensystem.

2.2

$\blacktriangleright$ Volumen des Spates berechnen

Nun sollst du das Volumen des Spates $ABCDEFGH$ berechnen. Mithilfe des Spatproduktes kann das Volumen berechnet werden, hierfür musst du allerdings erst einen Vektor für die Länge des Körpers festlegen, als auch für die Breite und die Höhe. Für die Länge nimmst du den Vektor $\overrightarrow{AB}$ , für die Breite den Vektor $\overrightarrow{AD}$ und für die Höhe den Vektor $\overrightarrow{AE}$ .

$V = (\overrightarrow{a}\times\overrightarrow{b})\cdot\overrightarrow{c}$

$\begin{array}[t]{rll} V&=&(\overrightarrow{AB}\times\overrightarrow{AD}) \cdot \overrightarrow{AE}\\[5pt] &=&\Biggl(\pmatrix{-1 \\ 3 \\ 1}\times\pmatrix{-4 \\ 0 \\ 0}\Biggr) \cdot \pmatrix{-2 \\ -2 \\ 6}\\[5pt] &=& \pmatrix{3\cdot0-1\cdot0 \\ 1\cdot (-4)-(-1)\cdot0 \\ (-1)\cdot0-3\cdot(-4)} \cdot \pmatrix{-2 \\ -2 \\ 6} \\[5pt] &=& \pmatrix{0 \\ -4 \\ 12}\cdot\pmatrix{-2 \\ -2 \\ 6} \\[5pt] &=& 0\cdot(-2)+(-4)\cdot(-2)+12\cdot6 \\[5pt] &=& 8+72 \\[5pt] &=& 80 \end{array}$

Somit beträgt das Volumen des Spates $V=80\text{[VE]}$ .

2.3

$\blacktriangleright$ Lagebeziehung Punkt Körper überprüfen

In dieser Aufgabe sollst du zeigen, dass der Punkt $P$ innerhalb des Spates $ABCDEFGH$ liegt und gleichzeitig auf der Geraden $g$ . Um dies zu beweisen, überprüfst du zuerst, ob der Punkt wirklich auf $g$ liegt. Dafür setzt du den Punkt mit der Geradengleichung gleich und überprüfst, ob es einen Wert für $t$ gibt, der jede Zeile erfüllt. Gilt dies, liegt $P$ auf $g$ . Danach berechnest du die Durchstoßpunkte der Geraden $g$ durch die Ebenen $ADHE$ und $BCGF$ . Dafür stellst du zuerst die beiden Ebenengleichungen in Parameterform auf. Anschließend berechnest du den Normalenvektor $\overrightarrow{n}$ der Ebenen, mit welchem du dann die Koordinatenform aufstellen kannst. Anhand der erhaltenen Werte für $t$ , kannst du dann überprüfen, ob der Punkt in dem Spat liegt.

$\begin{array}[t]{rll} \overrightarrow{OP}&=&\pmatrix{3 \\ -1 \\ 4} + t \cdot \pmatrix{-1 \\ 3 \\ 1}\\[5pt] \pmatrix{\frac{7}{4} \\ \frac{11}{4} \\ \frac{21}{4}}&=& \pmatrix{3 \\ -1 \\ 4} + t \cdot \pmatrix{-1 \\ 3 \\ 1} \end{array}$

Aus der ersten Zeile erhältst du folgende Gleichung:

$\frac{7}{4} = 3+ t \cdot (-1)$

Durch Äquivalenzumformungen ergibt sich $t_1=\frac{5}{4}$ .

$ADHE: \begin{array}[t]{rll} \overrightarrow{x}&=& \quad ... \end{array}$

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} \overrightarrow{n}&=&\pmatrix{-4 \\ 0 \\ 0}\times\pmatrix{-6 \\ -2 \\ 6} \\[5pt] &=&\pmatrix{0\cdot6-0\cdot(-2) \\ 0\cdot(-6)-(-4)\cdot6 \\ (-4)\cdot(-2)-0\cdot(-6)} \\[5pt] &=&\pmatrix{0 \\ 24 \\ 8} \end{array}$

$ADHE: \begin{array}[t]{rll} 0 &=& \overrightarrow{n}\circ[\overrightarrow{x}-\overrightarrow{OA}] \\[5pt] 0 &=& \overrightarrow{n}\circ\overrightarrow{x}-\overrightarrow{n}\circ\overrightarrow{OA} \\[5pt] 0 &=& 24x_2+8x_3-48 \\[5pt] 48 &=& 24x_2+8x_3 \end{array}$

Vollständige Lösung anzeigen

Somit lautet die Koordinatengleichung für die Ebene $ADHE$ : $24x_2+8x_3 = 48$ .

Analog gehst du nun für die zweite Ebene vor. Da die Ebenen parallel sind, besitzen sie den identischen Normalenvektor. Somit brauchst du diesen nicht erneut berechnen.

$BCGF: \begin{array}[t]{rll} 0 &=& \overrightarrow{n}\circ[\overrightarrow{x}-\overrightarrow{OB}] \\[5pt] 0 &=& \overrightarrow{n}\circ\overrightarrow{x}-\overrightarrow{n}\circ\overrightarrow{OB} \\[5pt] 0 &=& 24x_2+8x_3-128 \\[5pt] 128 &=& 24x_2+8x_3 \end{array}$

Vollständige Lösung anzeigen

Die Koordinatengleichung für die Ebene $BCGF$ lautet: $128=24x_2+8x_3$ .

Jetzt musst du den Parameter $t$ der Durchstoßpunkte berechnen. Hierfür setzt du die Gerade $g$ in die Koordinatengleichungen der beiden Ebenen ein.

$D_{ADHE}: \begin{array}[t]{rll} 48&=& 24 \cdot (-1+3t) + ... \\[5pt] \frac{1}{2} &=& t_2 \end{array}$

Vollständige Lösung anzeigen

$D_{BCGF}: \begin{array}[t]{rll} 128&=& 24 \cdot (-1+3t) + ... \\[5pt] \frac{3}{2} &=& t_3 \end{array}$

Vollständige Lösung anzeigen

Nun musst du nur noch $t_1$ mit $t_2$ und $t_3$ vergleichen. Da gilt $t_2\lt t_1\lt t_3$ , liegt der Punkt $P$ innerhalb des Spates. Somit hast du gezeigt, dass der Punkt $P$ sowohl auf $g$ liegt, als auch innerhalb des Spates.

2.4

$\blacktriangleright$ Abstand zweier Geraden berechnen

Du sollst bei dieser Aufgabe den Abstand der Kante $\overline{AE}$ zur Kante $\overline{BF}$ berechnen. Dazu bestimmst du zuerst die Geradengleichungen der Kante $\overline{AE}$ . Da die Flächen des Spates Parallelogramme sind, liegen die beiden Kanten parallel zueinander. Somit reicht es aus, den Abstand eines Punktes der Kante $\overline{BF}$ zur Geraden $\overrightarrow{g_1}$ zu berechnen.

$\overline{AE}: \begin{array}[t]{rll} \overrightarrow{g_1}&=& \overrightarrow{OA}+ t \cdot \overrightarrow{AE} \\[5pt] &=& \pmatrix{6 \\ 2 \\ 0}+ t \cdot \pmatrix{-2 \\ -2 \\ 6} \end{array}$

Damit du den Abstand des Punktes $B$ zur Geraden $g_1$ berechnen kannst, benötigst du einen Lotfußpunkt $L$ , welcher auf $g_1$ liegt. Mithilfe der Orthogonalitätsbedingung kannst du dann dessen genaue Koordinaten ermitteln und letztendlich den Abstand der beiden Kanten ausrechnen.

$L = (6-2t \mid 2-2t \mid 6t)$

Nun berechnest du den Verbindungsvektor $\overrightarrow{BL}$ .

$\begin{array}[t]{rll} \overrightarrow{BL}&=&\pmatrix{6-2t-5 \\ 2-2t-5 \\ 6t-1} \\[5pt] &=&\pmatrix{1-2t \\ -3-2t \\ -1+6t} \end{array}$

Du kannst nun mithilfe der Orhogonalitätsbedingung des Vektors $\overrightarrow{BL}$ und des Richtungsvektors der Geraden $g_1$ die Koordinaten des Lotfußpunktes $L$ ermitteln. Dafür muss das Skalarprodukt gleich Null sein.

$\begin{array}[t]{rll} \overrightarrow{BL} \circ \overrightarrow{AE}&=& 0 \\[5pt] \pmatrix{1-2t \\ -3-2t \\ -1+6t} \circ \pmatrix{-2 \\ -2 \\ 6}&=& 0 \\[5pt] t &=& \frac{1}{22} \end{array}$

Vollständige Lösung anzeigen

Die Koordinaten des Lotfußpunktes $L$ lauten also $L\left( \frac{65}{11} \mid \frac{21}{11} \mid \frac{6}{22}\right)$ . Nun musst du als letztes noch die Länge des Vektors $BL$ berechnen.

$\begin{array}[t]{rll} \mid BL \mid&=& \quad ... \end{array}$

Vollständige Lösung anzeigen

Der Abstand der Kanten $\overline{AE}$ und $\overline{BF}$ beträgt $\frac{2}{11}\sqrt{330}\text{[LE]}$ .

2.5

$\blacktriangleright$ Flächeninhalt Parallelogramm bestimmen

Um den Wert für $a$ zu ermitteln, musst du als erstes die Koordinaten des Punktes $R_a$ in Abhängigkeit von $a$ bestimmen. Die Geradengleichung für die Kante $\overline{AE}$ hast du bereits bestimmt. Danach berechnest du den Parameter $t$ in Abhängigkeit von $a$ . Hierfür setzt du die letzte Zeile der Geradengleichung gleich $a$ . Anschließend bestimmst du die Vektoren $\overrightarrow{AR_a}$ und $\overrightarrow{AB}$ . Um dann das $a$ bestimmen zu können, berechnest du den Betrag des Kreuzprodukts dieser beiden Vektoren und setzt es dem gegebenen Flächeninhalt $A$ gleich.

$\begin{array}[t]{rll} \overrightarrow{g_1}&=& \overrightarrow{OA}+ t \cdot \overrightarrow{AE} \\[5pt] &=& \pmatrix{6 \\ 2 \\ 0}+ t \cdot \pmatrix{-2 \\ -2 \\ 6} \end{array}$

$\begin{array}[t]{rll} 0+6t&=& a &\quad \scriptsize \mid\; :6 \\[5pt] t&=& \frac{a}{6} \end{array}$

Somit ist $t=\frac{a}{6}$ .

$\overrightarrow{AR_a}=\pmatrix{-2t \\ -2t \\ 6t}=\pmatrix{-\frac{1}{3}a \\ -\frac{1}{3}a \\ a}$

$\overrightarrow{AB}=\pmatrix{-1 \\ 3 \\ 1}$

$\begin{array}[t]{rll} \mid \overrightarrow{AR_a}\times\overrightarrow{AB} \mid&=& \frac{7}{3}\sqrt{30} \\[5pt] \left|\pmatrix{-\frac{1}{3}a \\ -\frac{1}{3}a \\ a} \times \pmatrix{-1 \\ 3 \\ 1}\right| &=& \frac{7}{3}\sqrt{30} \\[5pt] a &=& \frac{7}{2} \end{array}$

Vollständige Lösung anzeigen

Es ergibt sich für $a$ der Wert $a=\frac{7}{2}$ .

Bildnachweise [nach oben]

[1]