Wahlteil A3

Analysis und Stochastik

3.1

Gegeben ist die Funktion $f$ mit der Gleichung

$f(x)=(2x^2 + 8x)\cdot e^x$ mit $x\in\mathbb{R}$ .

Dein Graph ist $G$ .

Graf einer mathematischen Funktion mit Achsenbeschriftungen x und y.

Abb. 1

3.1.1

Berechne die Nullstellen von $f$ , die Koordinaten der lokalen Extrempunkte von $G$ .
Weise jeweils die Art de lokalen Extrempunkte nach.
Gib die benöigte Ableitungsfunktion an.

Begründe, dass sich die Art der Krümmung von $G$ im Intervall $-6\leq x\leq -2$ nicht ändert.

3.1.2

Zeige, dass die Funktion $F$ mit der Gleichung $F(X)=(2x^2+4x-4)\cdot e^x$ $(x\in\mathbb{R})$ eine Stammfunktion ist.

Der Graph $G$ und die $x-$ Achse begrenzen eine Fläche $A$ vollständig.
Berechne den Inhalt von $A$ .

3.1.3

Ermittle den Wert von $a$ $(a\in\mathbb{R}, -4\leq a\leq 0)$ , für den gilt: $\displaystyle\int_{a}^{0}f(x)\;\mathrm dx=e^a-4$ .

3.2

An der Hauptstraße einer Ortschaft regeln drei voneinander unabhängige Ampeln den Durchgangsverkehr. Jede der Ampeln zeigt mit der Wahrscheinlichkeit $0,7$ beim Heranfahren „grün“ an.
Die Zufallsvariable $X$ gibt die Anzahl der Ampeln bei einer Ortsdurchfahrt an, die „grün“ zeigen. $X$ wird als binominalverteilt angenommen.

3.2.1

Berechne die Wahrscheinlichkeitsverteilung von $X$ .
Stelle die Wahrscheinlichkeiten in einem Diagramm grafisch dar.

3.2.2

Bestimme die Anzahl von „grün“ anzeigenden Ampeln, mit denen man durchschnittlich bei dieser Ortsdurchfahrt rechnen muss.
Berechne die Standardabweichung von $X$ .

3.2.3

Ein Autofahrer trifft an keiner der drei Ampeln auf „grün“.
Entscheide, ob der Fahrer damit hätte rechnen müssen.
Begründe deine Entscheidung.

3.2.4

Zusätzlich und unabhängig wird hinter den bestehenden Ampeln eine vierte Ampel im Ort errichtet.
Berechne, mit welcher Mindestwahrscheinlichkeit die vierte Ampel „grün“ anzeigen muss, damit die Wahrscheinlichkeit einer Ortsdurchfahrt ohne Halt mindestens $0,3$ beträgt.

(35P)

Bildnachweise [nach oben]

[1]

3.1.1

$\blacktriangleright$ Nullstellen bestimmen

Du hast die Funktion $f$ gegeben und sollst deren Graph auf Nullstellen untersuchen. Um die Nullstellen von $f$ zu bestimmen musst du $f(x)=0$ setzen und nach $x$ auflösen. Die Funktion $f$ ist hierbei mit der Gleichung $f(x)=(2x^2+8x)\cdot \mathrm{e}^x$ gegeben.

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] (2x^2+8x)\cdot \mathrm{e}^x&=& 0 \\[5pt] \end{array}$

Hierbei kann man den Satz des Nullprodukts (Satz d. NP) anwenden. Das bedeutet, dass die Gleichung erfüllt ist, falls $2x^2+8x=0$ ist oder falls $\mathrm{e}^x=0$ ist. Von der $\mathrm{e}$ -Funktion wissen wir bereits, dass sie niemals den Wert $0$ annehmen kann. Deshalb genügt es $2x^2+8x=0$ zu betrachten.

$\begin{array}[t]{rll} 2x^2+8x&=& 0 &\quad \scriptsize \mid\;:2\\[5pt] x^2+4x&=& 0 &\quad \scriptsize \mid\; \text{mit }pq\text{ oder }abc\\[5pt] x_1&=& 0 \\[5pt] x_2&=& -4 \\[5pt] \end{array}$

Die Nullstellen des Graphen von $f$ liegen bei $x_1=0$ und $x_2=-4$ .

Extrempunkte bestimmen

Du hast die Funktion $f$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, f‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $f‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $f‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen $f‘$ und $f‘‘$ .
Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $f‘‘(x)$ einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
Berechne die Funktionswerte von $f$ an den Extremstellen.

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f(x)&=& (2x^2 +8x) \cdot \mathrm{e}^x \\[10pt] f‘(x)&=& (4x +8) \cdot \mathrm{e}^x + (2x^2 +8x) \cdot \mathrm{e}^x\\[5pt] &=& (2x^2 +12x +8) \cdot \mathrm{e}^x\\[10pt] f‘‘(x)&=& (4x +12) \cdot \mathrm{e}^x + (2x^2 +12x +8) \cdot \mathrm{e}^x \\[5pt] &=& (2x^2 +16x +20) \cdot \mathrm{e}^x \end{array}$

2. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $f‘(x)$ mit Null, erhältst du mögliche Extremstellen:

$\begin{array}[t]{rll} f‘(x)&=& 0 \\[5pt] (2x^2 +12x +8) \cdot \mathrm{e}^x&=& 0 &\quad \scriptsize \mid\; \text{Satz d. NP} \\[5pt] 2x^2 +12x +8&=& 0 &\quad \scriptsize \mid\;:2 \\[5pt] x^2 +6x +4&=& 0&\quad \scriptsize \mid\; \text{mit }pq\text{ oder }abc\\[5pt] x_1&=& -3 + \sqrt{5}\\[5pt] x_2&=& -3 - \sqrt{5} \end{array}$

3. Schritt: Hinreichendes Kriterium überprüfen

Hinreichendes Kriterium für $x_1= -3 + \sqrt{5}$ prüfen.

$\begin{array}[t]{rll} f‘‘(x_1)&=& (2x_1^2 +16x_1 +20) \cdot \mathrm{e}^{x_1} \\[5pt] &=& (2\cdot (-3+\sqrt{5})^2 +16\cdot (-3 + \sqrt{5}) +20) \cdot \mathrm{e}^{-3 + \sqrt{5}}\\[5pt] &\approx& 4,17 \quad \scriptsize \gt 0 \end{array}$

Somit besitzt der Graph von $f$ bei $x_1$ ein Minimum.

Hinreichendes Kriterium für $x_2= -3 + \sqrt{5}$ prüfen.

$\begin{array}[t]{rll} f‘‘(x_2)&=& (2x_2^2 +16x_2 +20) \cdot \mathrm{e}^{x_2} \\[5pt] &=& (2\cdot (-3-\sqrt{5})^2 +16\cdot (-3 - \sqrt{5}) +20) \cdot \mathrm{e}^{-3 - \sqrt{5}}\\[5pt] &\approx& -0,05 \quad \scriptsize \lt 0 \end{array}$

Somit besitzt der Graph von $f$ bei $x_2$ ein Maximum.

4. Schritt: Funktionswerte berechnen

Nun sollst du noch die Funktionswerte der Extrempunkte berechnen, um die Koordinaten der Extrempunkte anzugeben.

$\begin{array}[t]{rll} f(x_1)&=& (2x_1^2 +8x_1) \cdot \mathrm{e}^{x_1} \\[5pt] &=& (2\cdot (-3+\sqrt{5})^2 +8 \cdot (-3 + \sqrt{5})) \cdot \mathrm{e}^{-3 + \sqrt{5}}\\[5pt] &\approx& -2,3 \end{array}$

$\begin{array}[t]{rll} f(x_2)&=& (2x_2^2 +8x_2) \cdot \mathrm{e}^{x_2} \\[5pt] &=& (2\cdot (-3-\sqrt{5})^2 +8 \cdot (-3 - \sqrt{5})) \cdot \mathrm{e}^{-3 - \sqrt{5}}\\[5pt] &\approx& 0,06 \end{array}$

Der Graph von $f$ besitzt bei $(-3+\sqrt{5} \mid -2,3)$ ein Minimum und bei $(-3-\sqrt{5} \mid 0,06)$ ein Maximum.

Krümmung begründen

In dieser Teilaufgabe sollst du begründen, dass sich die Art der Krümmung von $G$ im Intervall $-6\leq x\leq -2$ nicht ändert. Du weißt bereits, dass sich die Krümmung nur einer Stelle $t$ ändern kann, für die gilt $f‘‘(t)=0$ . Bestimme somit alle Stellen $t$ mit $f‘‘(t)=0$ und überprüfe, ob eine dieser Stellen innerhalb des Intervalls $-6\leq x\leq -2$ liegt. Falls keine der Stellen im Intervall $-6\leq x\leq -2$ liegt hast du gezeigt, dass sich die Art der Krümmung nicht ändert.

$\begin{array}[t]{rll} f‘‘(t)&=& 0 \\[5pt] (2t^2 +16t +20) \cdot \mathrm{e}^{t}&=& 0 &\quad \scriptsize \mid\; \text{Satz d. NP} \\[5pt] 2t^2 +16t +20 &=& 0 &\quad \scriptsize \mid\;:2 \\[5pt] t^2 +8t +10&=& 0&\quad \scriptsize \mid\; \text{mit }pq\text{ oder }abc\\[5pt] t_{1/2} &=& -\frac{8}{2}\pm \sqrt{\left(\frac{8}{2} \right)^2 - 10 } \\[5pt] &=& -4 \pm \sqrt{6} \\[5pt] t_1&=& -4-\sqrt{6} \lt -6\\[5pt] t_2&=& -4+\sqrt{6} \gt -2 \end{array}$

Die Stellen, in denen sich die Krümmung ändert, befinden sich außerhalb des Intervalls $[-6;-2].$ Innerhalb dieses Intervalls ändert sich die Krümmung daher nicht.

3.1.2

$\blacktriangleright$ Stammfunktion zeigen

In dieser Aufgabe sollst du zeigen, dass die Funktion $F(x)=(2x^2+4x-4)\cdot \mathrm{e}^x$ eine Stammfunktion von $f$ ist. Berechne dazu die Stammfunktionen von $f$ mit partieller Integration.

Hierbei musst du zweimal wie folgt partiell Integrieren.

$\begin{array}[t]{rll} \displaystyle\int_{a}^{b} (2x^2+8x)\cdot \mathrm e^{x}\;\mathrm dx &=& \left[(2x^2+8x)\cdot (\mathrm e^{x})\right]_a^b- \displaystyle\int_{a}^{b} (4x +8)\cdot (\mathrm e^{x})\;\mathrm dx &\quad \scriptsize \\[5pt] &=& \left[(2x^2+8x)\cdot (\mathrm e^{x})\right]_a^b- \left[(4x +8)\cdot (\mathrm e^{x})\right]_a^b +\displaystyle\int_{a}^{b} 4\cdot \mathrm e^{x}\;\mathrm dx &\quad \scriptsize \\[5pt] &=&\left[(2x^2 +4x-8)\cdot (\mathrm e^{x})\right]_a^b+\left[4 \cdot \mathrm e^{x} + C\right]_a^b &\quad \scriptsize \\[5pt] &=& \left[(2x^2 +4x-4)\cdot (\mathrm e^{x})\right]_a^b&\quad \scriptsize \\[5pt] \end{array}$

Die Stammfunktion $F(x)$ ist somit mit $F(x)=(2x^2+4x-4) \cdot e^x$ gegeben.

Fläche berechnen

In dieser Teilaufgabe sollst du den Flächeninhalt berechnen, die der Graph der Funktion $f$ und die $x$ -Achse vollständig begrenzen. Im oberen Aufgabenteil hast du bereits die Nullstellen bestimmt. Nun kannst du diese Nullstellen als Grenzen deines Integrals wählen, da du den Flächeninhalt der Fläche berechnen sollst, die der Graph von $f$ und die $x$ -Achse vollständig begrenzen. Daraus folgt für die gesuchte Fläche $A$ :

$A = \left|\displaystyle\int_{a}^{b}\left(f(x)\right)\mathrm dx \right|$

Nun kannst du die Nullstellen als Grenzen einsetzen und mit dem Hauptsatz der Integralrechnung die Fläche $A$ berechnen.

$\begin{array}[t]{rll} A&=& \left|\displaystyle\int_{a}^{b}\left(f(x)\right)\mathrm dx \right| &\quad \scriptsize \\[5pt] &=& \left|\displaystyle\int_{-4}^{0}\left(2x^2+8x\right)\cdot (\mathrm e^{x}) \; \mathrm dx \right| &\quad \scriptsize \\[5pt] &=& \left|\left[(2x^2+4x-4)\cdot (\mathrm e^{x})\right]_{-4}^0 \right|&\quad \scriptsize \\[5pt] &=& \left|(2\cdot (0)^2+4\cdot (0)-4)\cdot \mathrm e^{0})- (2\cdot (-4)^2+4\cdot (-4)-4)\cdot \mathrm e^{-4})\right|\\[5pt] &\approx& 4,22 \\[5pt] \end{array}$

Der Flächeninhalt beträgt somit etwa $4,22$ FE.

3.1.3

$\blacktriangleright$ Wert ermitteln

In dieser Aufgabe sollst du den Wert für $a$ ermitteln, für den gilt $\displaystyle\int_{a}^{0} f(x)\;\mathrm dx=e^a -4$ . Berechne nun erneut den Flächeninhalt mit dem Hauptsatz der Integralrechnung und löse nach $a$ auf.

$\begin{array}[t]{rll} e^a -4&=& \displaystyle\int_{a}^{0}\left(f(x)\right)\mathrm dx &\quad \scriptsize \\[5pt] e^a -4&=& \displaystyle\int_{a}^{0}\left(2x^2+8x\right)\cdot (\mathrm e^{x}) \; \mathrm dx &\quad \scriptsize \\[5pt] e^a -4&=& \left[(2x^2+4x-4)\cdot (\mathrm e^{x})\right]_{a}^0 &\quad \scriptsize \\[5pt] e^a -4&=& (2\cdot (0)^2+4\cdot (0)-4)\cdot \mathrm e^{0})- (2\cdot (a)^2+4\cdot (a)-4)\cdot \mathrm e^{a})\\[5pt] e^a -4&=& -4 - (2\cdot a^2 +4\cdot a-4) \cdot e^a &\quad \scriptsize \mid \; +4 \\[5pt] e^a&=&- (2\cdot a^2 +4\cdot a-4) \cdot e^a &\quad \scriptsize \mid \; -e^a \\[5pt] 0&=& (-2\cdot a^2 -4\cdot a+3) \cdot e^a &\quad \scriptsize \mid\; \text{Satz d. NP} \\[5pt] 0&=& -2\cdot a^2 -4\cdot a+3&\quad \scriptsize \mid\; :(-2) \\[5pt] 0&=& a^2 +2\cdot a-1,5&\quad \scriptsize \mid\; \text{mit }pq\text{ oder }abc\\[5pt] a_1&\approx& 0,58\\[5pt] a_2&\approx& -2,58\\[5pt] \end{array}$

Da in der Aufgabenstellung gegeben ist, dass $-4\leq a\leq0$ gilt, kann man den Wert für $a_2$ vernachlässigen und und es gilt $a=-2,58$ .

3.2.1

$\blacktriangleright$ Wahrscheinlichkeitsverteilung berechnen

In dieser Aufgabe sollst du die Wahrscheinlichkeitsverteilung der Zufallsvariablen $X$ berechnen und diese anschließend in einem geigneten Diagramm darstellen. Hierbei hast du gegeben, dass die Zufallsvariable $X$ als binomialverteilt angenommen werden kann. $X$ kann hierbei nur zwischen $0$ und $3$ liegen, da maximal $3$ Ampeln und minimal $0$ Ampeln „grün“ zeigen können. Somit sind die Wahrscheinlichkeiten $P(X=0)$ , $P(X=1)$ , $P(X=2)$ und $P(X=3)$ gesucht. Die Wahrscheinlichkeitsfunktion ist hierbei folgendermaßen gegeben:

$P(X=k) = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}$

In diesem Fall ist $n$ die Anzahl der Ampeln ( $n=3$ ), $X$ die Anzahl der Ampeln, die „grün“ zeigen und $p$ die Wahrscheinlichkeit dafür, dass eine Ampel „grün“ zeigt ( $p = 0,7$ ).

Somit folgen für die Wahrscheinlichkeiten:

$\begin{array}[t]{rll} P(X=0)&=& \binom{3}{0} \cdot 0,7^0 \cdot (1-0,7)^{3-0} \\[5pt] &=& \binom{3}{0} \cdot 0,7^0 \cdot (0,3)^{3} \\[5pt] &=& 0,027 \\[5pt] \end{array}$

$\begin{array}[t]{rll} P(X=1)&=& \binom{3}{1} \cdot 0,7^1 \cdot (1-0,7)^{3-1} \\[5pt] &=& \binom{3}{1} \cdot 0,7^1 \cdot (0,3)^{2} \\[5pt] &=& 0,189 \\[5pt] \end{array}$

$\begin{array}[t]{rll} P(X=2)&=& \binom{3}{2} \cdot 0,7^2 \cdot (1-0,7)^{3-2} \\[5pt] &=& \binom{3}{2} \cdot 0,7^2 \cdot (0,3)^{1} \\[5pt] &=& 0,441 \\[5pt] \end{array}$

$\begin{array}[t]{rll} P(X=3)&=& \binom{3}{3} \cdot 0,7^3 \cdot (1-0,7)^{3-3} \\[5pt] &=& \binom{3}{3} \cdot 0,7^3 \cdot (0,3)^{0} \\[5pt] &=& 0,343 \\[5pt] \end{array}$

Die Wahrscheinlichkeiten kannst du nun beispielsweise in einem Säulendiagramm darstellen.

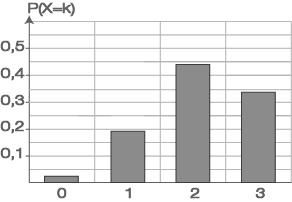Säulendiagramm zeigt Wahrscheinlichkeiten für verschiedene Werte von X.

Abb. 1: Wahrscheinlichkeitsverteilung

3.2.2

$\blacktriangleright$ Erwartungswert und Standardabweichung bestimmen

In dieser Aufgabe sollst du die durchschnittliche Anzahl von „grün“ anzeigenden Ampeln berechnen, mit denen man bei einer Ortsdurchfahrt rechnen muss. Dies entspricht dem Erwartungswert. Außerdem sollst du noch die Standardabweichung berechnen.

Für den Erwartungswert gilt folgende Formel:

$E(X) = x_1 \cdot P(X=x_1) +x_2\cdot P(X=x_2) +x_3\cdot P(X=x_3) + x_4 \cdot P(X=x_4)$

Dadurch folgt für den Erwartungswert:

$\begin{array}[t]{rll} E(X)&=& x_1 \cdot P(X=x_1) +x_2\cdot P(X=x_2) +x_3\cdot P(X=x_3) + x_4 \cdot P(X=x_4) \\[5pt] &=& 0 \cdot P(X=0) +1\cdot P(X=1) +2\cdot P(X=2) + 3 \cdot P(X=3) \\[5pt] &=& 0,189 +2\cdot 0,441 + 3 \cdot 0,343 \\[5pt] &=& 2,1\\[5pt] \end{array}$

Mit dem Erwartungswert kannst du nun die Standardabweichung $\sigma(X)$ mit folgender Formel berechnen:

$\sigma(X) =\sqrt{ (x_1-E(X))^2 \cdot P(X=x_1) + ... + (x_4-E(X))^2 \cdot P(X=x_4)}$

Für die Standardabweichung gilt:

$\begin{array}[t]{rll} \sigma(X)^2&=& (x_1-E(X))^2 \cdot P(X=x_1) + (x_2-E(X))^2 \cdot P(X=x_2) + \\[5pt] &&(x_3-E(X))^2 \cdot P(X=x_3)+(x_4-E(X))^2 \cdot P(X=x_4) \\[5pt] \sigma(X)^2&=& (0-2,1)^2 \cdot 0,027 + (1-2,1)^2 \cdot 0,189 + \\[5pt] && (2-2,1))^2 \cdot 0,441+(3-2,1)^2 \cdot 0,343 \\[5pt] \sigma(X)^2&=& 0,63 &\quad \scriptsize \mid \, \sqrt{}\\[5pt] \sigma(X)&=&\sqrt{0,63} \\[5pt] &\approx& 0,79 \\[5pt] \end{array}$

Somit sind bei einer Ortsdurchfahrt durchschnittlich mit $2,1$ Ampeln zu rechnen und die Standardabweichung beträgt ungefähr $0,79$ .

3.2.3

$\blacktriangleright$ Entscheidung begründen

In dieser Aufgabe sollst du entscheiden, ob ein Autofahrer damit rechnen muss, dass bei einer Ortsdurchfahrt keine der drei Ampeln „grün“ zeigt. Der Erwartungswert beträgt hierbei $2,1$ grüne Ampeln und die Standardabweichung ist mit $0,79$ gegeben. Der Autofahrer muss nicht damit rechnen, dass keine der drei Ampeln grün zeigt, da dies eine sehr starke Abweichung zum Erwartungswert ist und deshalb dieser Fall sehr unwahrscheinlich ist. Dieser Fall kann aber durchaus auftreten, dass bedeutet, dass es zwar sehr unwahrscheinlich aber dennoch möglich ist, dass der Fall auftritt.

3.2.4

$\blacktriangleright$ Mindestwahrscheinlichkeit bestimmen

In dieser Aufgabe wird eine unabhängige vierte Ampel im Ort errichtet. Nun sollst du die Mindestwahrscheinlichkeit dafür bestimmen, dass die vierte Ampel „grün“ zeigt, wenn man mit einer Wahrscheinlichkeit von mindestens $0,3$ ohne Halt durch den ganzen Ort fährt. Das bedeutet, dass die Wahrscheinlichkeit dafür, dass alle Ampeln „grün“ zeigen mit $0,3$ gegeben ist. Diese Wahrscheinlichkeit berechnet sich, indem man alle Einzelwahrscheinlichkeit miteinander multipliziert. Dadurch folgt:

$\begin{array}[t]{rll} P(X=4)&=& p_1 \cdot p_2 \cdot p_3 \cdot p_4\\[5pt] 0,3&=& 0,7 \cdot 0,7 \cdot 0,7 \cdot p_4 \\[5pt] 0,3&=& 0,343 \cdot p_4 &\quad \scriptsize \mid \, :0,343 \\[5pt] p_4&=& 0,875 \end{array}$

Die Mindestwahrscheinlichkeit, dass die vierte Ampel „grün“ zeigt liegt somit bei $0,875$ .

Bildnachweise [nach oben]

[1]