2 Analysis
2.1
Die Abbildung 1 zeigt die Graphen der in 
definierten Funktionen 
und 
mit 
und 
Die beiden Graphen haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der
-Achse.
definierten Funktionen und mit und
Die beiden Graphen haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der
-Achse.
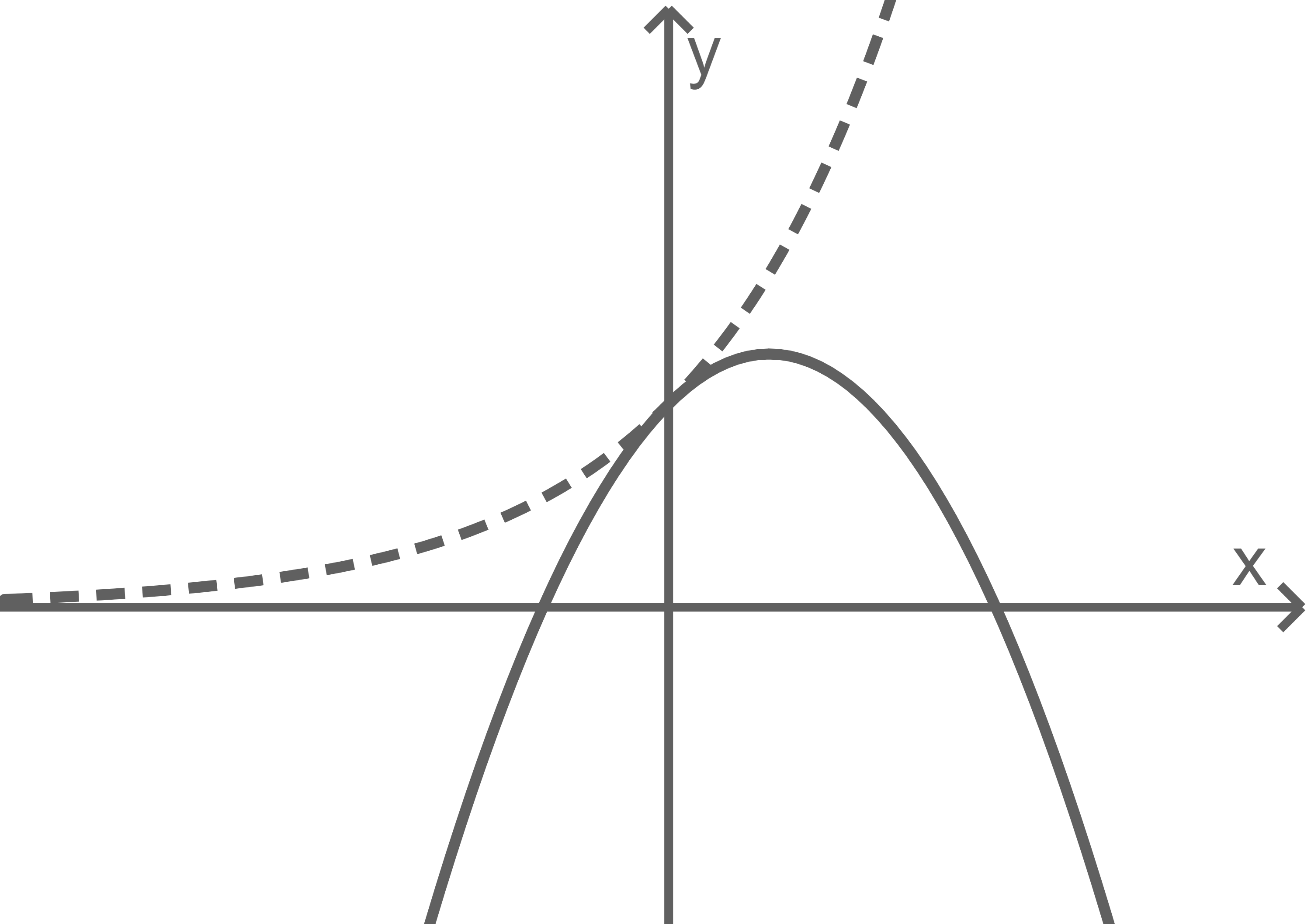
Abbildung 1
2.1.1
Berechne die Nullstellen und die Extremstelle von 
(3 BE)
2.1.2
Beschreibe, wie man den Abstand zwischen dem Graphen von und der Gerade mit der Gleichung 
berechnen könnte.
und der Gerade mit der Gleichung berechnen könnte.
(2 BE)
2.1.3
Berechne die Größe des Winkels, in dem der Graph von die Gerade mit der Gleichung schneidet.
die Gerade mit der Gleichung schneidet.
(4 BE)
2.1.4
Zeige, dass die Graphen von und in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
und in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
(4 BE)
2.1.5
Berechne den Inhalt des Flächenstücks, das die Graphen von und und die Gerade mit der Gleichung 
begrenzen.
und und die Gerade mit der Gleichung begrenzen.
(4 BE)
2.2
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in definierte Funktion 
beschreibt für 
die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist 
die seit Beobachtungsbeginn vergangene Zeit in Sekunden und 
die momentane Durchflussrate in Kubikmetern pro Sekunde.
Die Abbildung 2 zeigt den Graphen von
Die in
definierte Funktion beschreibt für die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und die momentane Durchflussrate in Kubikmetern pro Sekunde.
Die Abbildung 2 zeigt den Graphen von
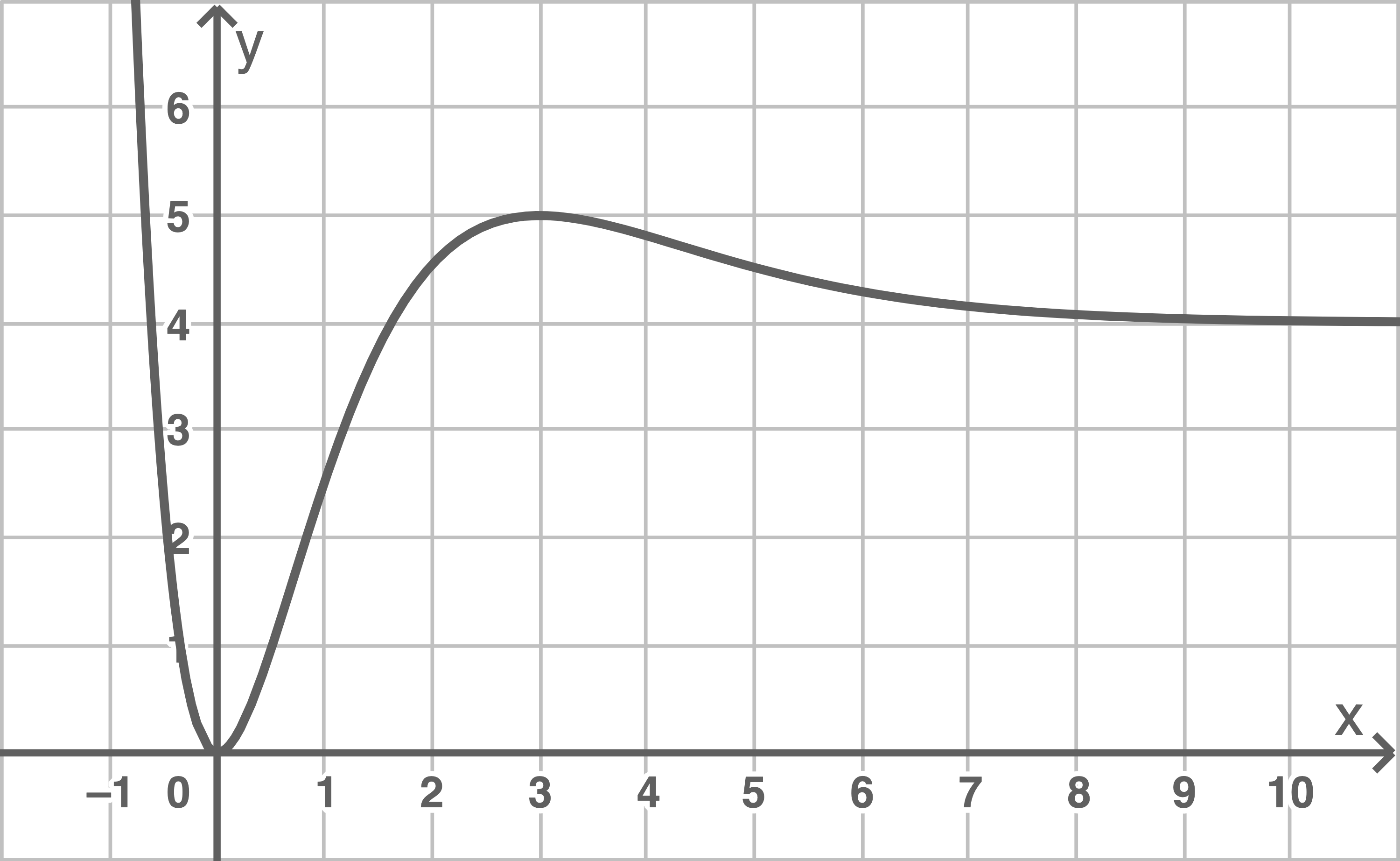
Abbildung 2
2.2.1
Ermittle mithilfe der Abbildung 2 das Volumen des Wassers, das vom Zeitpunkt vier Sekunden nach Beobachtungsbeginn bis zum Zeitpunkt sechs Sekunden nach Beobachtungsbeginn an der Messstelle vorbeifließt.
(3 BE)
2.2.2
Bestimme für die ersten elf Sekunden nach Beobachtungsbeginn mithilfe der Abbildung 2 die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt.
(3 BE)
2.2.3
Die Tangente an den Graphen von im Punkt 
wird durch die Gleichung 
dargestellt. Interpretiere die folgende Aussage im Sachzusammenhang:
Für alle Werte von ![\(x \in[0,7 ; 1,4]\)](https://www.schullv.de/resources/formulas/33433d08b4b8e623af15cb856a50b067fabd9869023da6aadb4d6566d6f30339_light.svg)
gilt 
im Punkt wird durch die Gleichung dargestellt. Interpretiere die folgende Aussage im Sachzusammenhang:
Für alle Werte von gilt
(3 BE)
2.3
Für jeden Wert von 
ist eine in definierte Funktion 
mit 
gegeben. Unabhängig von 
sind 
und 
die einzigen Extremstellen von . Die Funktion 
ist die in der Aufgabe 2.2 betrachtete Funktion , die Abbildung 2 zeigt also den Graphen von 
ist eine in definierte Funktion mit gegeben. Unabhängig von sind und die einzigen Extremstellen von . Die Funktion ist die in der Aufgabe 2.2 betrachtete Funktion , die Abbildung 2 zeigt also den Graphen von
2.3.1
Beschreibe den Einfluss des Parameters auf den Graphen von 
auf den Graphen von
(1 BE)
2.3.2
Bestimme denjenigen Wert von 
für den der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des Graphen von auf der -Achse liegt.
für den der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des Graphen von auf der -Achse liegt.
(4 BE)
2.3.3
Berechne den Wert des Terms 
Gib alle Werte von an, für die genau eine Nullstelle hat.
Gib alle Werte von an, für die genau eine Nullstelle hat.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1.1
Nullstellen berechnen
Extremstelle berechnen
Mit dem notwendigen Kriterium für Extremstellen folgt:
![\(\begin{array}[t]{rll}
r](https://www.schullv.de/resources/formulas/3764c937e7148b317eba49d9d8d50a50fb9eb6358dab97f564e4d05b90ff785c_light.svg)
Da es sich beim Graphen von um eine Parabel handelt, muss es eine Extremstelle geben. Auf die Überprüfung des hinreichenden Kriteriums kann also verzichtet werden. Die Extremstelle von ist 
![\(\begin{array}[t]{rll}
r(x) &=& 0 \\[5pt]
&...& \\[5pt]
x_{1,2}&=& \frac{1}{2}\pm \sqrt{ \frac{5}{4}} \\[5pt]
&=& \frac{1\pm\sqrt{5}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/c926eefba350d8c21e9528136179603b7e9f35e19ebc83751681fa345f04eb92_light.svg)
![\(\begin{array}[t]{rll}
r(x) &=& 0 \\[5pt]
-(x^2-x-1)&=& 0 \quad \scriptsize \mid\;\cdot (-1) \\[5pt]
x^2 -x-1 &=& 0 \quad \scriptsize \mid\; pq\text{-Formel} \\[5pt]
x_{1,2}&=& -\frac{-1}{2}\pm \sqrt{\left( \frac{-1}{2}\right)^2 -(-1)} \\[5pt]
&=& \frac{1}{2}\pm \sqrt{ \frac{5}{4}} \\[5pt]
&=& \frac{1\pm\sqrt{5}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/5c9c6eb2954eda9d61c8c9714130e3b2c99da282b552457402240e0e6ff41835_light.svg)
Mit dem notwendigen Kriterium für Extremstellen folgt:
Da es sich beim Graphen von um eine Parabel handelt, muss es eine Extremstelle geben. Auf die Überprüfung des hinreichenden Kriteriums kann also verzichtet werden. Die Extremstelle von ist
2.1.2
Die Gerade mit der Gleichung verläuft parallel zur -Achse. Ihr Abstand 
zur nach unten geöffneten Parabel, die durch 
beschrieben wird, entspricht also dem Abstand der Geraden zum höchsten Punkt der Parabel. Wird die -Koordinate dieses höchsten Punkts mit 
bezeichnet, kann der Abstand wie folgt bestimmt werden:
verläuft parallel zur -Achse. Ihr Abstand zur nach unten geöffneten Parabel, die durch beschrieben wird, entspricht also dem Abstand der Geraden zum höchsten Punkt der Parabel. Wird die -Koordinate dieses höchsten Punkts mit bezeichnet, kann der Abstand wie folgt bestimmt werden:
2.1.3
1. Schritt: Schnittstelle berechnen
![\(\begin{array}[t]{rll}
s(x) &=& 4 \\[5pt]
\mathrm e^x &=& 4 &\quad \scriptsize \mid\;\ln \\[5pt]
x &=& \ln (4)
\end{array}\)](https://www.schullv.de/resources/formulas/878bbeba9fe26b463078460ffe279b7acb362de5c91a0d364b92193b1278111c_light.svg)
2. Schritt: Schnittwinkel berechnen
Da die Gerade mit der Gleichung parallel zur -Achse verläuft, entspricht der Schnittwinkel des Graphen von mit der Geraden dem Steigungswinkel des Graphen von in der Schnittstelle.
Mit der Formel für den Steigungswinkel 
folgt:
![\(\begin{array}[t]{rll}
\tan (\alpha) &=& s](https://www.schullv.de/resources/formulas/b6001980d9d8d2e413148f31b084123f247735d83f6ce30753f6b6c68680f5c5_light.svg)
Der Winkel, unter dem der Graph von die Gerade mit der Gleichung schneidet, ist ca. 
groß.
2. Schritt: Schnittwinkel berechnen
Da die Gerade mit der Gleichung parallel zur -Achse verläuft, entspricht der Schnittwinkel des Graphen von mit der Geraden dem Steigungswinkel des Graphen von in der Schnittstelle.
Mit der Formel für den Steigungswinkel folgt:
Der Winkel, unter dem der Graph von die Gerade mit der Gleichung schneidet, ist ca. groß.
2.1.4
In der Aufgabenstellung ist angegeben, dass sich der gemeinsame Punkt auf der -Achse befindet. Für ihn gilt also 
Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen:
Es gilt also 
und 
An der Stelle 
haben die Graphen von und daher eine gemeinsame Tangente mit der Gleichung:
-Achse befindet. Für ihn gilt also
Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen:
Es gilt also und An der Stelle haben die Graphen von und daher eine gemeinsame Tangente mit der Gleichung:
2.1.5
Der Inhalt des Flächenstücks, das die Graphen von und mit der -Achse und der Gerade mit der Gleichung einschließen, beträgt 
![\( A= \mathrm e^2-\frac{7}{3}\; \text{[FE]}\)](https://www.schullv.de/resources/formulas/6597102a6217d0c5d7176d799dbc212671515e16d33b7f9497b06301df0e0fd3_light.svg)
![\(\begin{array}[t]{rll}
A &=& \displaystyle\int_{0}^{2}(s(x)-r(x))\;\mathrm dx \\[5pt]
&=& \displaystyle\int_{0}^{2}(\mathrm e^x-(-(x^2-x-1)))\;\mathrm dx \\[5pt]
&=& \displaystyle\int_{0}^{2}(\mathrm e^x+x^2-x-1)\;\mathrm dx \\[5pt]
&=& \left[\mathrm e^x+\frac{1}{3}x^3-\frac{1}{2}x^2-x\right]_0^2\\[5pt]
&=& \mathrm e^2+\frac{1}{3}\cdot 2^3-\frac{1}{2}\cdot 2^2-2 -\left( \mathrm e^0+\frac{1}{3}\cdot 0^3-\frac{1}{2}\cdot 0^2-0\right)\\[5pt]
&=& \mathrm e^2+\frac{8}{3}- 4 -1 \\[5pt]
&=& \mathrm e^2-\frac{7}{3} \; \text{[FE]} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/035d5e04ad43cfc277dc276b7656276c9997bd70915c682c5367ded623697662_light.svg)
und mit der -Achse und der Gerade mit der Gleichung einschließen, beträgt
2.2.1
Die gesuchte Menge Wasser entspricht dem Inhalt der Fläche, die der Graph von mit der -Achse und den Geraden mit den Gleichungen 
und 
einschließt.
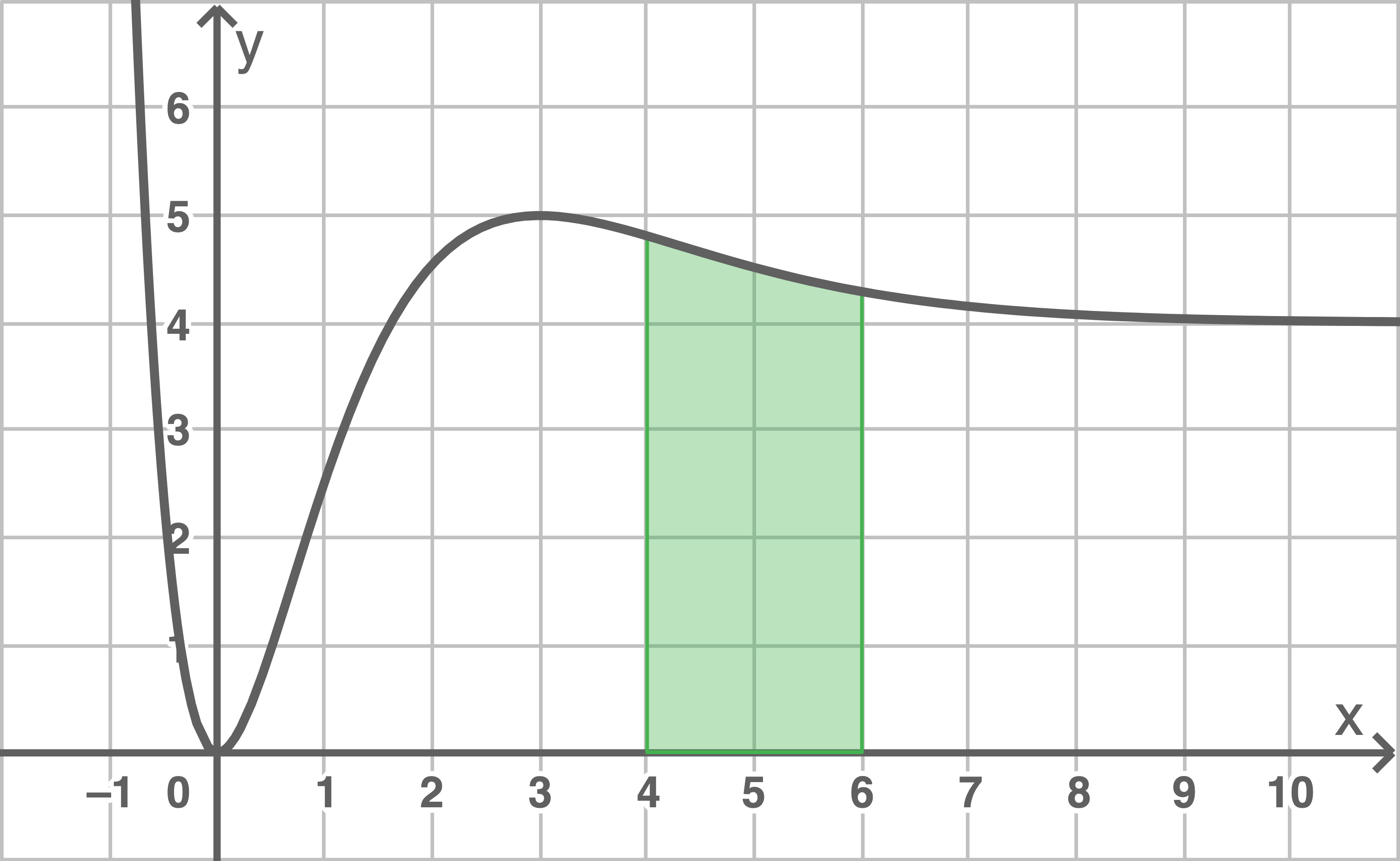Anhand der Abbildung lässt sich dieser Flächeninhalt zu ca. 
abschätzen.
Im betrachteten Zeitraum fließen also ca. 
Wasser an der Messstelle vorbei.
mit der -Achse und den Geraden mit den Gleichungen und einschließt.
abschätzen.
Im betrachteten Zeitraum fließen also ca. Wasser an der Messstelle vorbei.
2.2.2
Der Wendepunkt im betrachteten Zeitraum, in dem der Graph von fällt, wird aus der Abbildung abgelsen und hat circa die Koordinaten 
Damit beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa 
fällt, wird aus der Abbildung abgelsen und hat circa die Koordinaten
Damit beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa
2.2.3
Im Zeitraum von 
Sekunden nach Beobachtungsbeginn bis 
Sekunden nach Beobachtungsbeginn beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer maximalen relativen Abweichung von 
Sekunden nach Beobachtungsbeginn bis Sekunden nach Beobachtungsbeginn beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer maximalen relativen Abweichung von
2.3.1
Eine Veränderung des Werts von bewirkt eine Verschiebung des Graphen von 
in -Richtung.
bewirkt eine Verschiebung des Graphen von in -Richtung.
2.3.2
Die Extremstellen von sind laut Aufgabenstellung und 
Damit der Mittelpunkt der Strecke zwischen den beiden Extrempunkten auf der -Achse liegt, muss folgendes gelten:
sind laut Aufgabenstellung und
Damit der Mittelpunkt der Strecke zwischen den beiden Extrempunkten auf der 
-Achse liegt, muss folgendes gelten:
![\(\begin{array}[t]{rll}
\frac{1}{2}\cdot (w_a(0)+w_a(3)) &=& 0 \\[5pt]
& ... & \\[5pt]
a &=& 2-10\mathrm e^{-3}
\end{array}\)](https://www.schullv.de/resources/formulas/ccd16100f2f57f57d1e79ce4ba83a0b2d6ddb3596d8e8639993a90351416ab2b_light.svg)
![\(\begin{array}[t]{rll}
\frac{1}{2}\cdot (w_a(0)+w_a(3)) &=& 0 \\[5pt]
\frac{1}{2}\cdot \left(-4+a +20\mathrm e^{-3}+a\right) &=& 0 \\[5pt]
\frac{1}{2}\cdot \left(-4+2a +20\mathrm e^{-3}\right) &=& 0 &\quad \scriptsize \mid\; \cdot 2\\[5pt]
-4+2a +20\mathrm e^{-3} &=& 0 &\quad \scriptsize \mid\; +4;-20\mathrm e^{-3}\\[5pt]
2a &=& 4-20\mathrm e^{-3}&\quad \scriptsize \mid\; :2 \\[5pt]
a &=& 2-10\mathrm e^{-3}
\end{array}\)](https://www.schullv.de/resources/formulas/2a6ba71cea43df96a13d26ce2909113a9721763e413279310a81905f05bf5008_light.svg)
2.3.3
hat für 
und für 
genau eine Nullstelle.