1 Analysis – Pflichtaufgabe

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit der Gleichung $f(x)=4x^3-30x^2+54x.$

Die Abbildung 1 zeigt den Graphen von $f.$

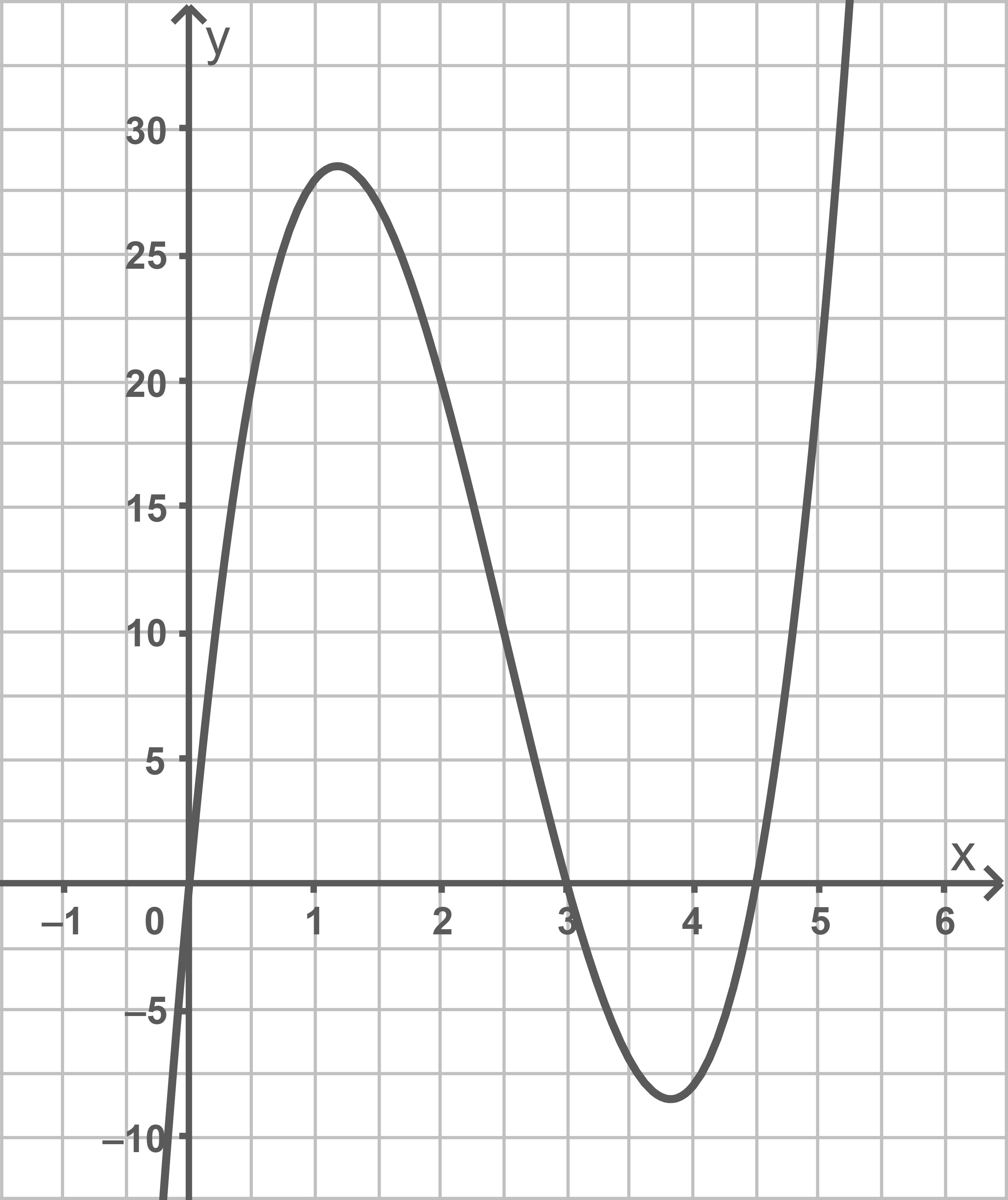
Graph einer mathematischen Funktion mit Achsenbeschriftungen und Raster.

Abbildung 1

1.1

Zeige rechnerisch, dass $3$ eine Nullstelle von $f$ ist.

Gib die Koordinaten des Schnittpunktes des Graphen von $f$ mit der $y$ -Achse an.

(2 BE)

1.2

Der Graph von $f$ besitzt genau einen Wendepunkt.

1.2.1

Ermittle rechnerisch die Koordinaten des Wendepunkts.

(3 BE)

1.2.2

Gib alle Werte des Definitionsbereiches an, für die der Graph von $f$ rechtsgekrümmt ist.

(2 BE)

1.3

Berechne den Wert des Terms $\displaystyle\int_{2}^{3}f(x)\;\mathrm dx.$

(2 BE)

1.4

Beurteile mithilfe der Abbildung die folgende Aussage:

Der Inhalt des vom Graphen von $f$ und der $x$ -Achse im 4. Quadranten eingeschlossenen Flächenstücks ist größer als $\textit{15}.$

(3 BE)

1.5

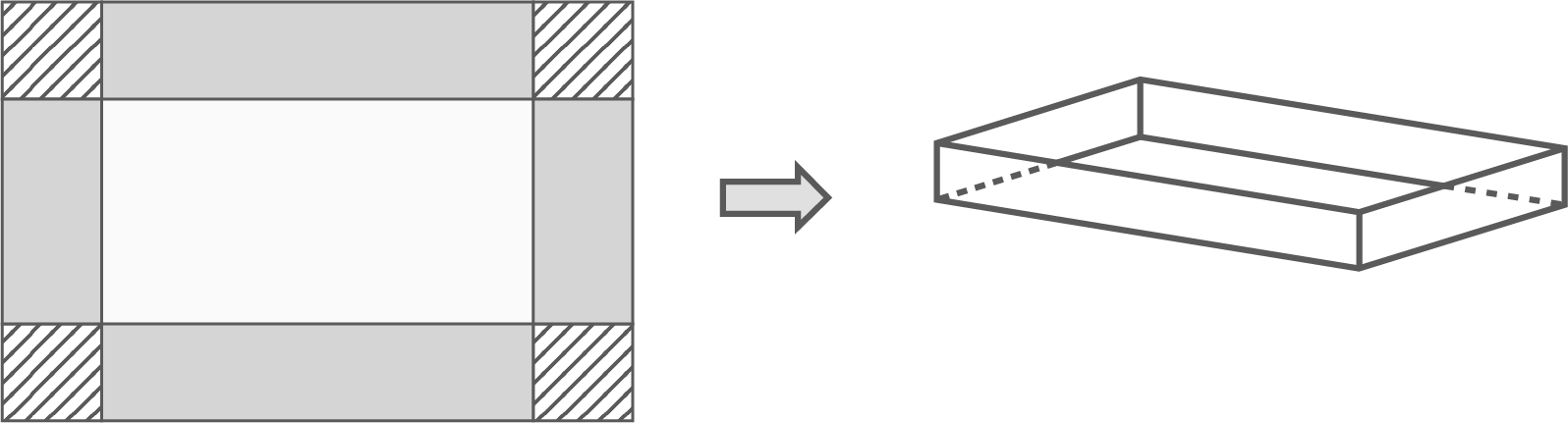
Aus einem rechteckigen Stück Pappe mit den Seitenlängen $6\;\text{dm}$ und $9\;\text{dm}$ soll eine oben offene Schachtel gefertigt werden (siehe Abbildung 2). Dazu werden an jeder Ecke dieser Pappe gleich große quadratische Stücke der Seitenlänge $x$ herausgeschnitten. Diese Stücke sind in der Abbildung 2 schraffiert dargestellt. Die grau gefärbten Teile der Pappe werden nach oben gefaltet und mit Klebestreifen zusammengeklebt.

Diagramm zeigt die Umwandlung eines Rechtecks in eine dreidimensionale Form.

Abbildung 2

Für bestimmte Werte von $x$ modelliert die Funktion $f$ aus den vorherigen Teilaufgaben das Volumen einer solchen Schachtel. Dabei ist $f$ das Volumen in Kubikdezimeter $(\text{dm}^3)$ und $x$ die Seitenlänge der herausgeschnittenen quadratischen Stücke in $\text{dm}.$

1.5.1

Bestätige rechnerisch, dass das Volumen einer solchen Schachtel durch den Term $4x^3-30x^2+54x$ der Funktion $f$ beschrieben wird.

Gib alle für diese Modellierung möglichen Werte von $x$ an und begründe deine Angabe.

(5 BE)

1.5.2

Verdeutliche durch Eintragungen in Abbildung 1, dass das Volumen einer solchen Schachtel für die Werte $x=0,5$ und $x=2$ identisch ist.

(2 BE)

1.5.3

Unter allen möglichen Schachteln hat eine das maximale Volumen.

Berechne mithilfe der Funktion $f$ die Abmessungen dieser Schachtel und gib das zugehörige Volumen an.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Zeigen der Nullstelle $\boldsymbol{x=3}$

$\begin{array}[t]{rlll} f(3)&=&4\cdot3^3-30\cdot3^2+54\cdot3 \\[5pt] &=&108-270+162 \\[5pt] &=&0 \end{array}$

Koordinaten des Schnittpunktes des Graphen mit der $\boldsymbol{y}$ -Achse ermitteln
Um die Koordinaten des Schnittpunktes $S_y$ des Graphen von $f$ mit der $y$ -Achse zu bestimmen, wird $x=0$ in $f(x)$ eingesetzt:

$\begin{array}[t]{rlll} f(0)&=&4\cdot0-30\cdot0+54\cdot0 \\[5pt] &=&0 \end{array}$

Somit hat der Schnittpunkt die Koordinaten $S_y(0\mid0).$

1.2

1.2.1

Um die Koordinaten des Wendepunkts zu bestimmen, werden zunächst die erste und zweite Ableitung von $f$ mithilfe der Potenzregel ermittelt:

$\(f$

Notwendige Bedingung für Wendepunkte anwenden

$\(\begin{array}[t]{rlll} f$

Da laut Aufgabenstellung genau ein Wendepunkt existiert, kann die Überprüfung der hinreichenden Bedingung hier vernachlässigt werden.

$\boldsymbol{y}$ -Koordinate des Wendepunkts bestimmen

$\begin{array}[t]{rlll} f(2,5)&=&4\cdot2,5^3-30\cdot2,5^2+54\cdot2,5 \\[5pt] &=&10 \end{array}$

Somit hat der Wendepunkt die Koordinaten $(2,5\mid10).$

1.2.2

Anhand der Koordinaten des Wendepunkts ist in Abbildung 1 erkennbar, dass der Graph von $f$ für $x\lt2,5$ rechtsgekrümmt ist.

1.3

Der Wert des Integrals von $f$ kann mithilfe der Stammfunktion bestimmt werden:

$\begin{array}[t]{rlll} \displaystyle\int_{2}^{3}f(x)\;\mathrm dx&=&\displaystyle\int_{2}^{3}4x^3-30x^2+54x\;\mathrm dx \\[5pt] &=&\Bigl[x^4-10x^3+27x^2\Bigr]_2^3 \\[5pt] &=&54-44 \\[5pt] &=&10 \end{array}$

1.4

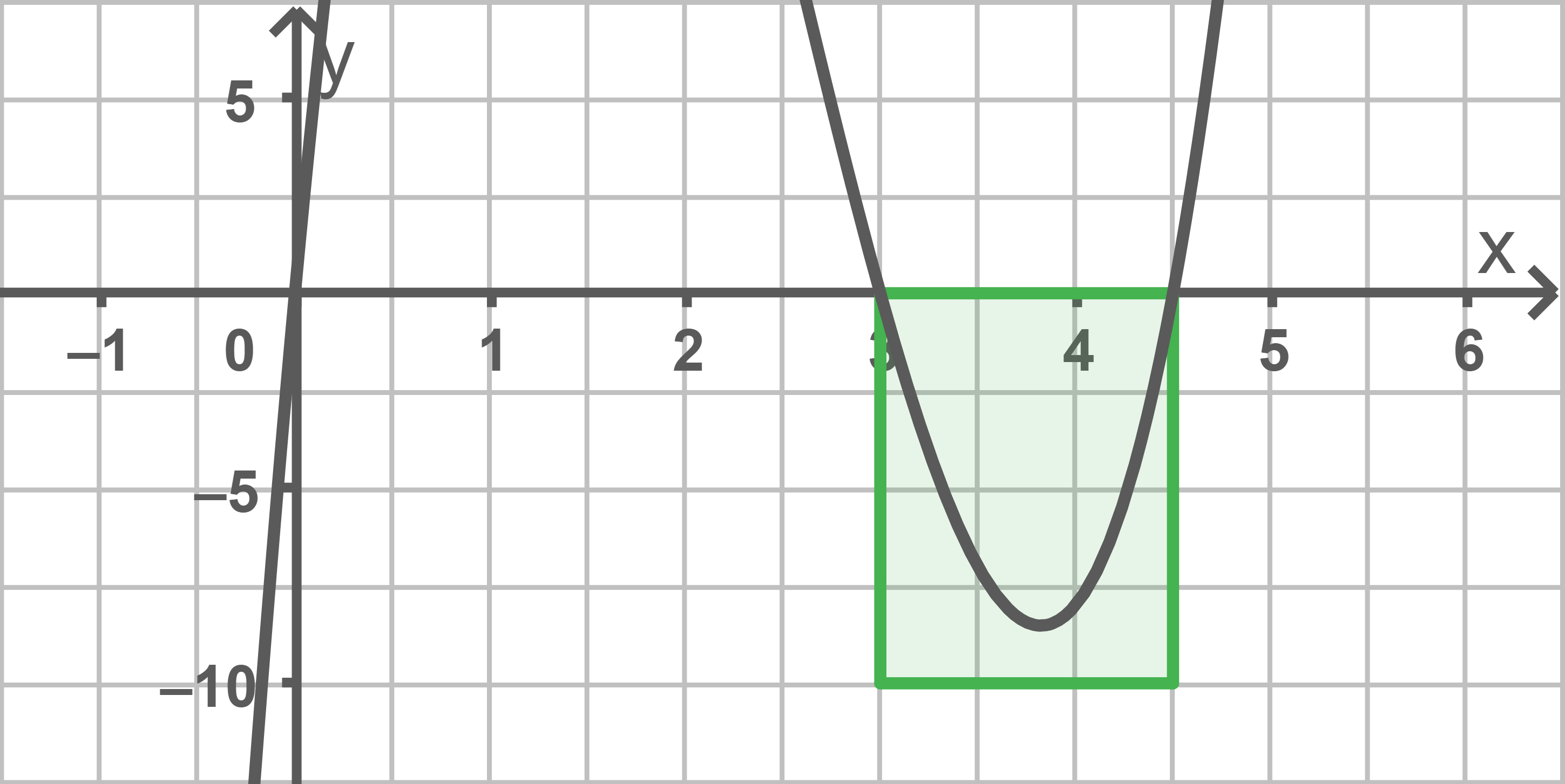
Grafik eines Koordinatensystems mit einer Parabel und einem markierten Bereich.

Bei dem betrachteten Flächenstück im 4. Quadranten handelt es sich um das Flächenstück, das zwischen dem Graphen von $f$ und der $x$ -Achse zwischen $x=3$ und $x=4,5$ eingeschlossen wird. Es liegt innerhalb des Rechtecks mit den Seitenlängen $1,5$ und $10.$ Somit folgt, dass der Inhalt des Flächenstücks kleiner als $15$ ist.

Alternativ können auch die Kästchen des betrachteten Flächenstücks gezählt werden, was eine Fläche von etwa $6$ Kästchen ergibt. Daraus folgt ein Flächeninhalt von $6\cdot0,5\cdot2,5=7,5.$

Die Aussage ist somit falsch.

1.5

1.5.1

Beschreibung des Volumens der Schachtel durch $\boldsymbol{f(x)}$
Für das Volumen eines Quaders gilt:

$V=a\cdot b\cdot c$

An jeder Ecke wird ein quadratisches Stück der Seitenlänge $x$ herausgeschnitten. Somit gilt:

$a=6-2x;$ $b=9-2x;$ $c=x$

Für das Volumen der Schachtel folgt:

$\begin{array}[t]{rlll} V(x)&=&(6-2x)\cdot(9-2x)\cdot x \\[5pt] &=&54x-12x^2-18x^2+4x^3 \\[5pt] &=&4x^3-30x^2+54x \end{array}$

Mögliche Werte von $\boldsymbol{x}$ für die Modellierung angeben
Im Intervall $0\lt x\lt3$ sind die Funktionswerte positiv, somit sind dort alle Werte von $x$ für Schachteln modellierbar. Hingegen sind Quadrate mit $x\gt3$ nicht herausschneidbar.

1.5.2

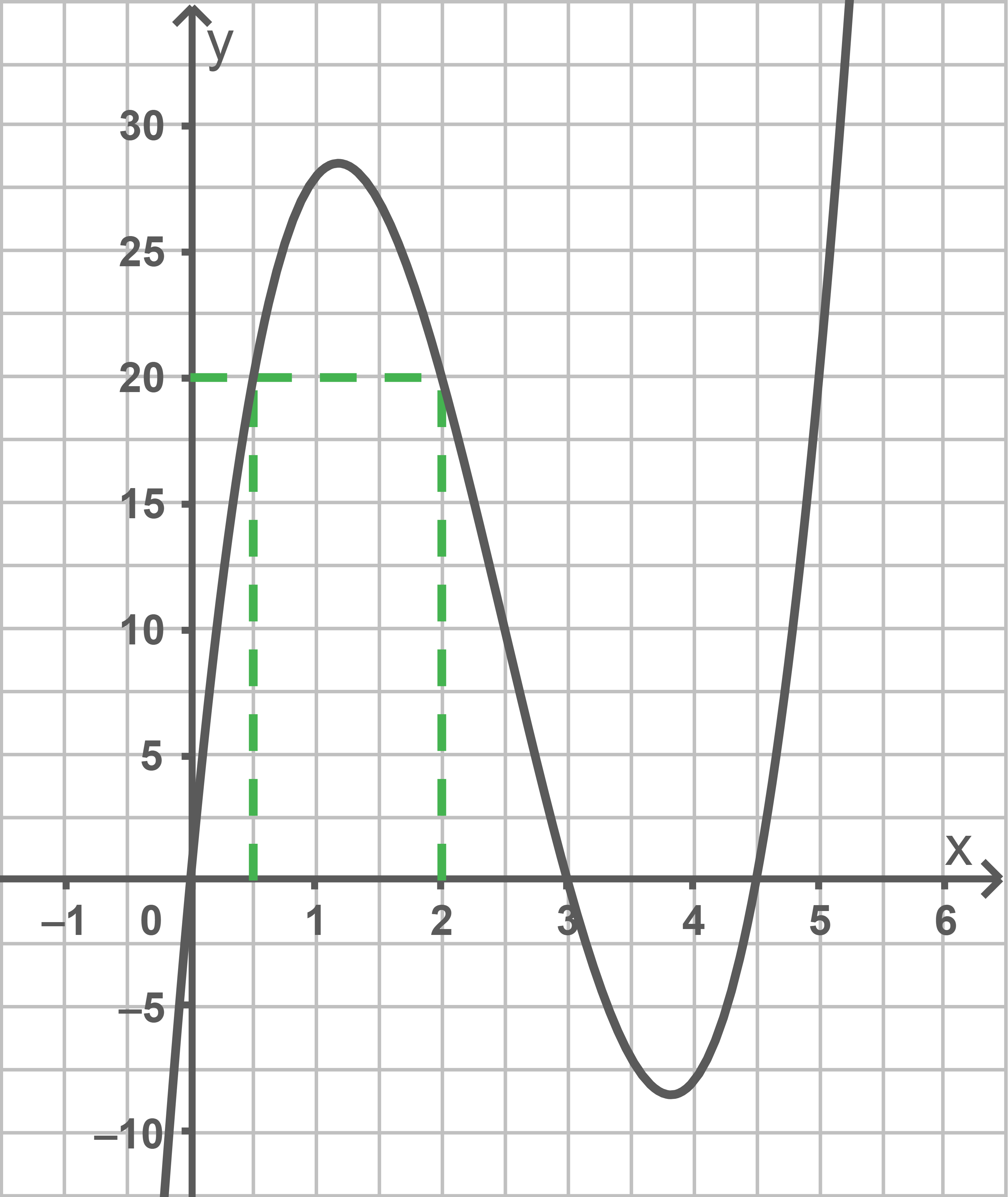
Graph einer Funktion mit grünen Markierungen und Koordinatenachsen.

Sowohl für $x=0,5$ als auch $x=2$ beträgt das Volumen der Schachtel $20\;\text{dm}^3.$

1.5.3

Notwendige Bedingung für Extrempunkte anwenden

$\(\begin{array}[t]{rlll} f$

Mithilfe der $pq$ -Formel können die Lösungen berechnet werden:

$\begin{array}[t]{rlll} x_{1,2}&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt] &=&\dfrac{5}{2}\pm\sqrt{\left(-\dfrac{5}{2}\right)^2-\dfrac{9}{2}} \\[5pt] &=&\dfrac{5}{2}\pm\sqrt{\dfrac{7}{4}} \end{array}$

Der Abbildung 1 ist zu entnehmen, dass das Maximum im Intervall $[0;3]$ liegt. Somit entfällt $x_1=\tfrac{5}{2}+\sqrt{\tfrac{7}{4}}\approx3,82$ als Lösung.

Berechnung der Abmessungen und des Volumens
Die Abmessungen und das Volumen der Schachtel können mithilfe des Funktionsterms von $f(x)$ und $x_2\approx1,18$ berechnet werden:

$\begin{array}[t]{rlll} a&=&6-2x_2&\approx&3,65 \\[3pt] b&=&9-2x_2&\approx&6,65 \end{array}$

$\begin{array}[t]{rlll} f(x_2)&=&f(1,18) \\[5pt] &=&4\cdot1,18^3-30\cdot1,18^2+54\cdot1,18 \\[5pt] &\approx&28,5 \end{array}$

Somit hat die Schachtel eine Länge von $6,65\;\text{dm},$ eine Breite von $3,65\;\text{dm}$ und eine Höhe von $1,18\;\text{dm}$ bei einem maximalen Volumen von $28,5\;\text{dm}^3.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?