Wahlaufgaben

4 Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{1}{8}x^3-\frac{3}{8}x^2-1.$

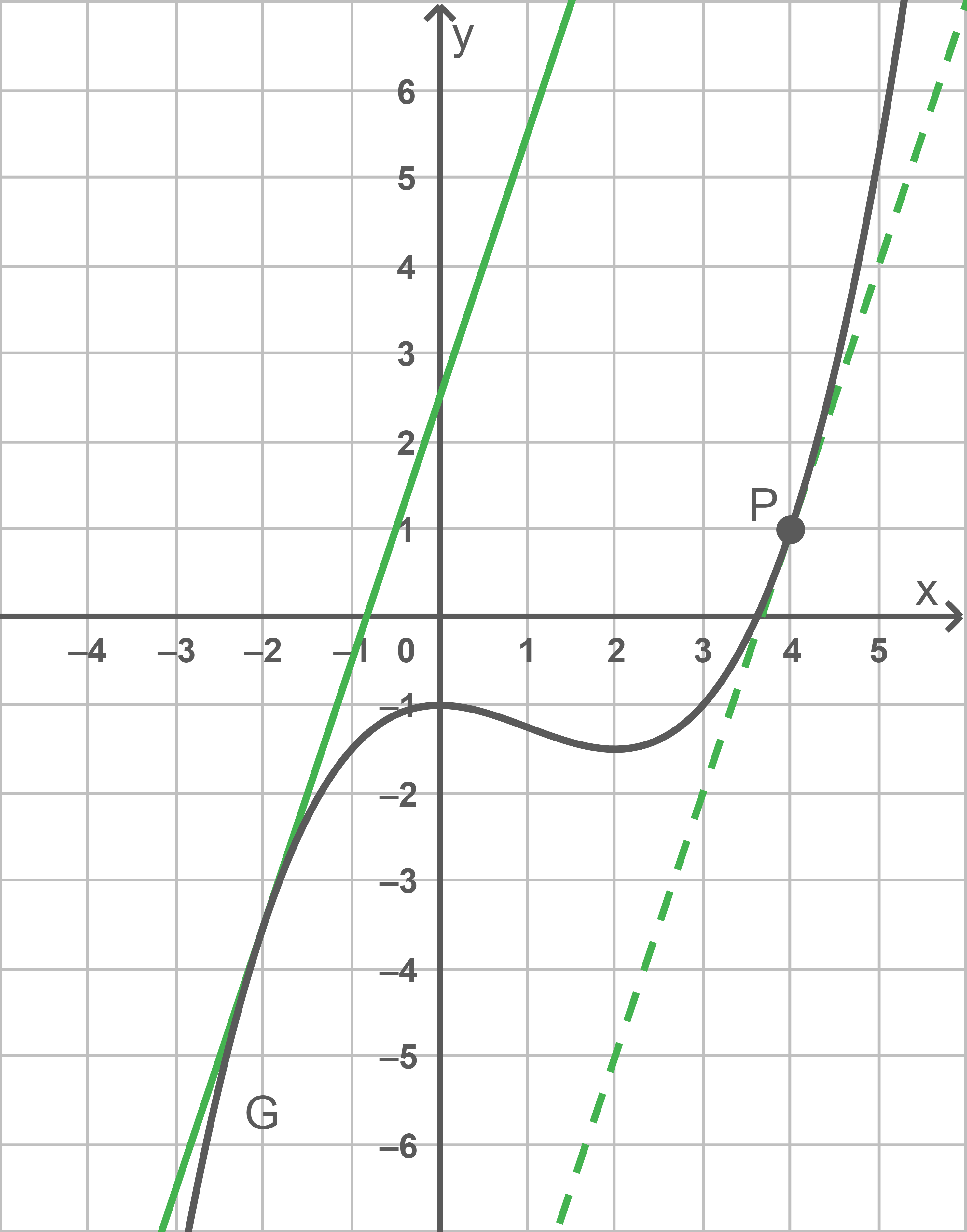
Die Abbildung zeigt den Graphen $G$ von $f.$
Die Tangente an $G$ im Punkt $P(4\mid1)$ wird mit $t$ bezeichnet.

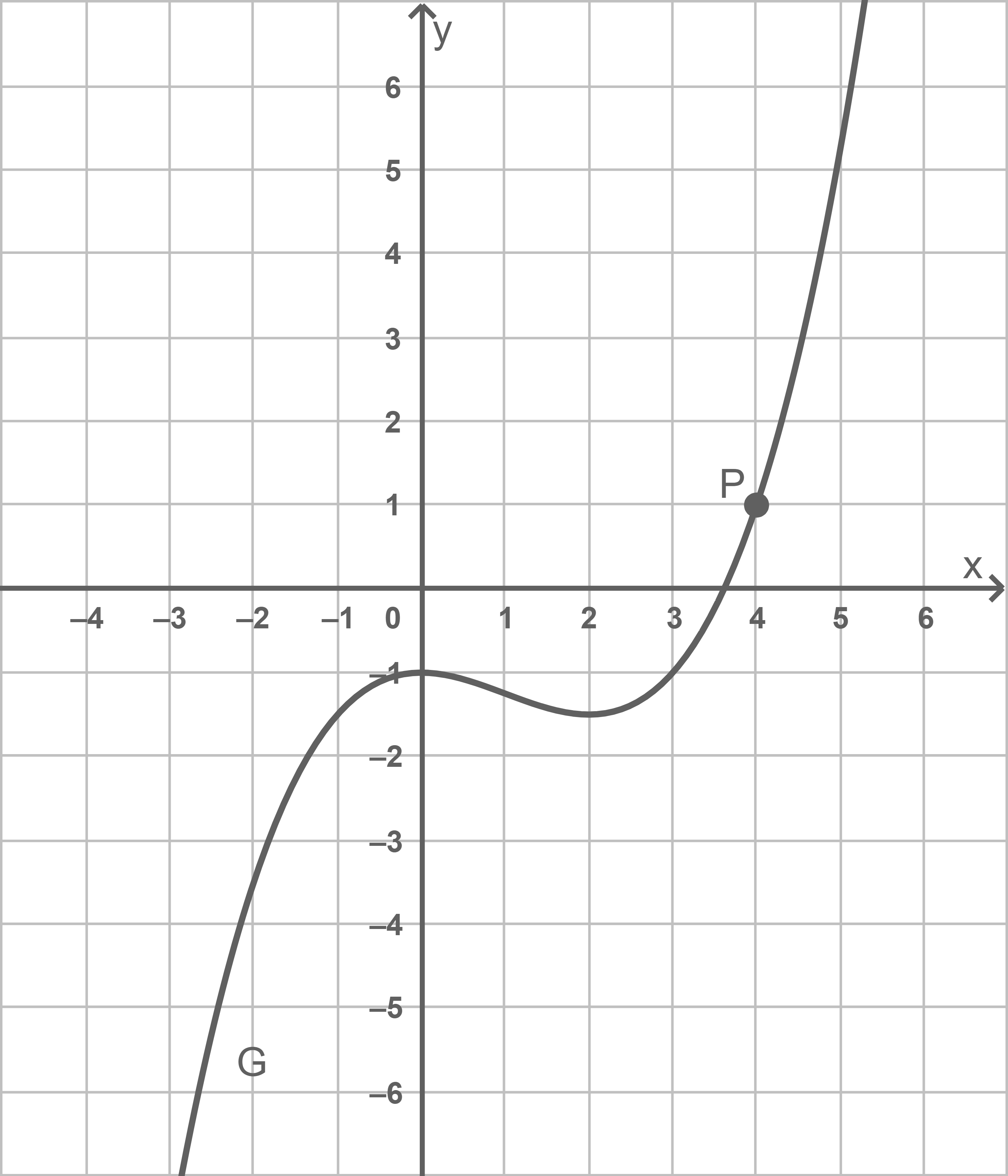
Graf einer mathematischen Funktion im Koordinatensystem mit markierten Punkten P und G.

4.1

Bestimme rechnerisch eine Gleichung von $t.$

(3 BE)

4.2

Es gibt genau eine weitere Tangente an $G,$ die parallel zu $t$ verläuft.

Skizziere diese in der Abbildung.

(2 BE)

5 Analytische Geometrie

Gegeben sind die Punkte $P(0\mid-1\mid1)$ und $Q(2\mid5\mid3).$

5.1

Durch Spiegelung des Punktes $P$ am Punkt $Q$ entsteht der Punkt $\(P$

Ermittle die Koordinaten von $\(P$

(2 BE)

5.2

Die Ebene E hat die Gleichung $E:\;x+3y+z=20.$ Weise nach, dass $Q$ in $E$ liegt und der Vektor $\overrightarrow{PQ}$ ein Normalenvektor von $E$ ist.

(3 BE)

6 Stochastik

Ein auf künstlicher Intelligenz (KI) basierender Bilderkennungsalgorithmus soll für eine Verkehrsüberwachung alle Objekte, die sich im Bild einer Kamera bewegen, in die Kategorien "Fußgänger" und "Sonstige Verkehrsteilnehmende" einteilen. Die Polizei weiß aus Erfahrung, dass im Kreuzungsbereich, der von dieser Kamera überwacht wird, $10\,\%$ der Verkehrsteilnehmenden Fußgänger sind.

Nach einer Testphase werden die Ergebnisse analysiert, die mit der KI gewonnen wurden. Es zeigte sich, dass $95\,\%$ der Fußgänger, aber auch $2\,\%$ der sonstigen Verkehrsteilnehmenden von der KI als Fußgänger kategorisiert werden.

6.1

Stelle die möglichen Ergebnisse dieser Untersuchung in einem vollständig beschrifteten Baumdiagramm dar.

(3 BE)

6.2

Mit dem Term $\frac{0,1\cdot0,95}{0,1\cdot0,95+0,9\cdot0,02}$ kann eine Wahrscheinlichkeit für ein Ereignis im Sachzusammenhang berechnet werden. Gib dieses Ereignis an.

(2 BE)

7 Analysis

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ mit $f(x)=\mathrm{e}^x$ und $g$ mit $g(x)=-\mathrm{e}^x.$

7.1

Die Abbildung zeigt die Graphen der Funktionen $f$ und $g.$

Begründe mithilfe der Abbildung, dass gilt:
$\displaystyle\int_{0}^{1}f(x)\;\mathrm dx\gt1,5.$

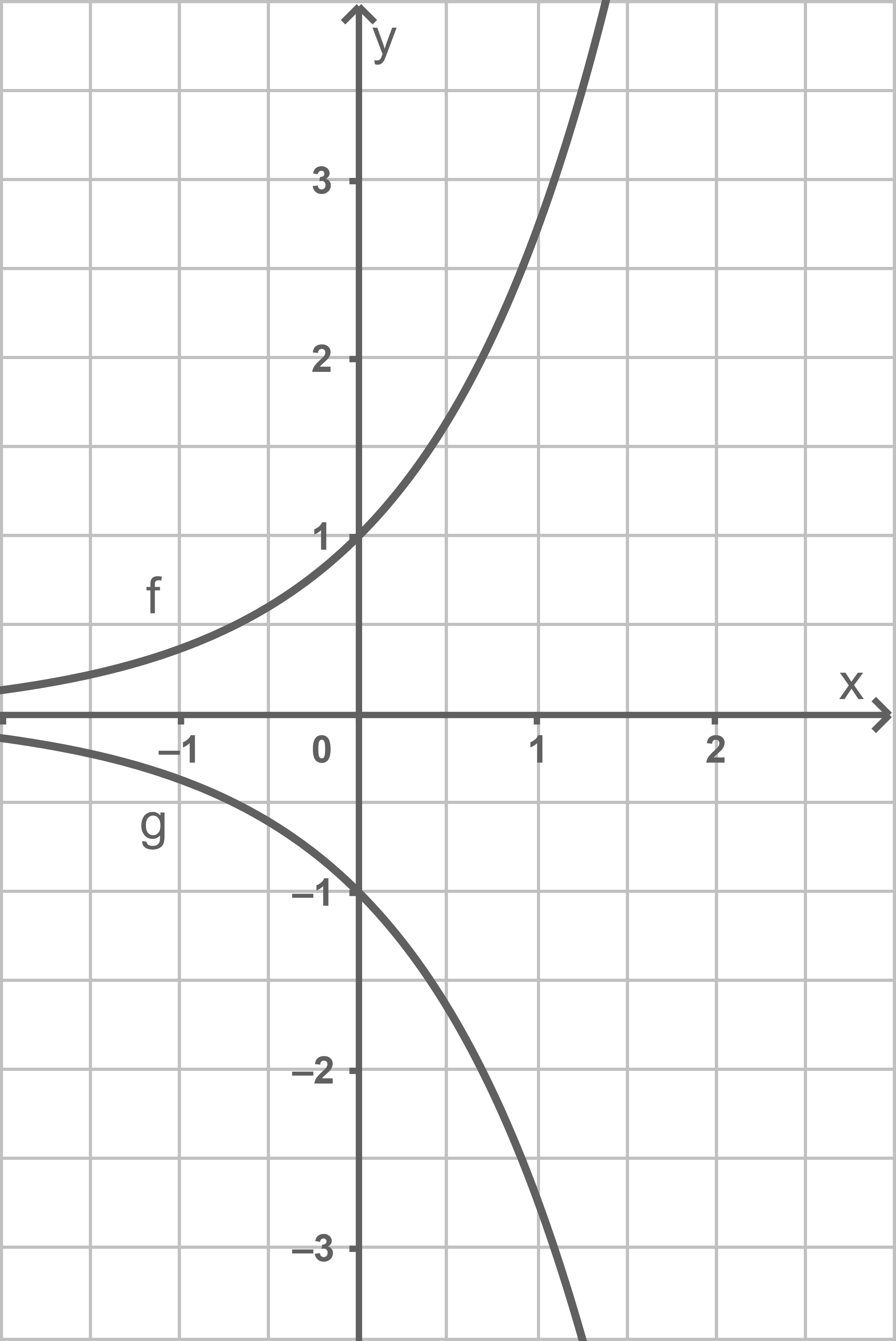
Graph von zwei Funktionen f und g im Koordinatensystem mit Achsen und Gittern.

(2 BE)

7.2

Die Tangente an den Graphen von $f$ an der Stelle $a,\;a\in\mathbb{R},$ heißt $t_f$ und die Tangente an den Graphen von $g$ an der Stelle $a$ heißt $t_g.$
Ermittle den Wert von $a,$ für den die Tangenten $t_f$ und $t_g$ einen rechten Winkel bilden.

(3 BE)

8 Analytische Geometrie

Das Quadrat $ABCD$ ist Grundfläche einer geraden Pyramide, deren Spitze $S$ im Koordinatenursprung liegt.

$M(0\mid0\mid5)$ ist der Mittelpunkt des Quadrats. Der Punkt $P(2\mid-2\mid4)$ liegt auf der Seitenkante $\overline{BS}$ der Pyramide.

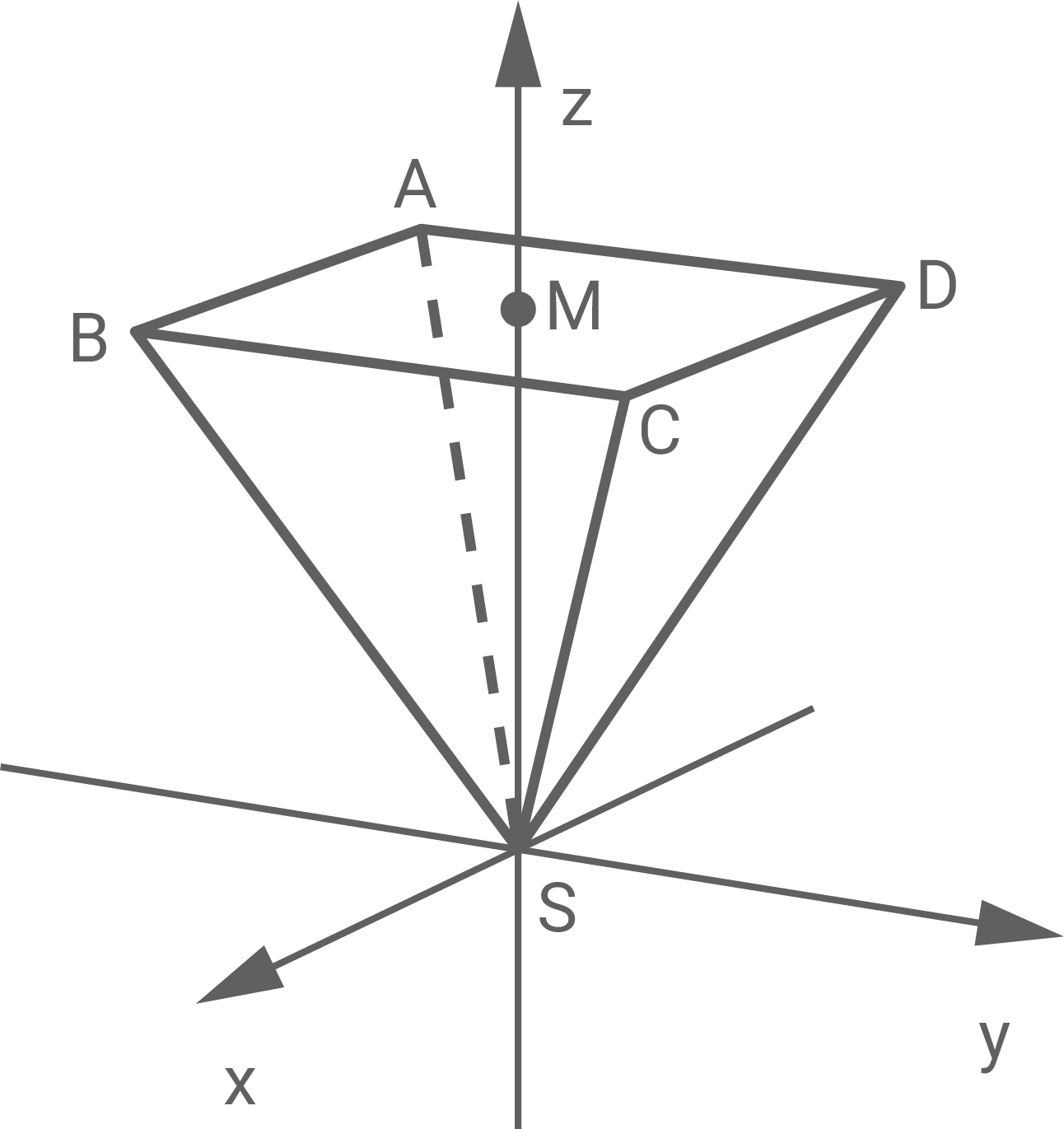
Grafische Darstellung eines Kegels im Koordinatensystem mit Achsen x, y, z und Punkten A, B, C, D, M, S.

8.1

Gib eine Gleichung der Ebene an, in der die Grundfläche der Pyramide liegt.

(1 BE)

8.2

Ermittle den Flächeninhalt der Grundfläche.

(4 BE)

9 Stochastik

Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $X$ mit den Parametern $n$ und $p=0,5.$

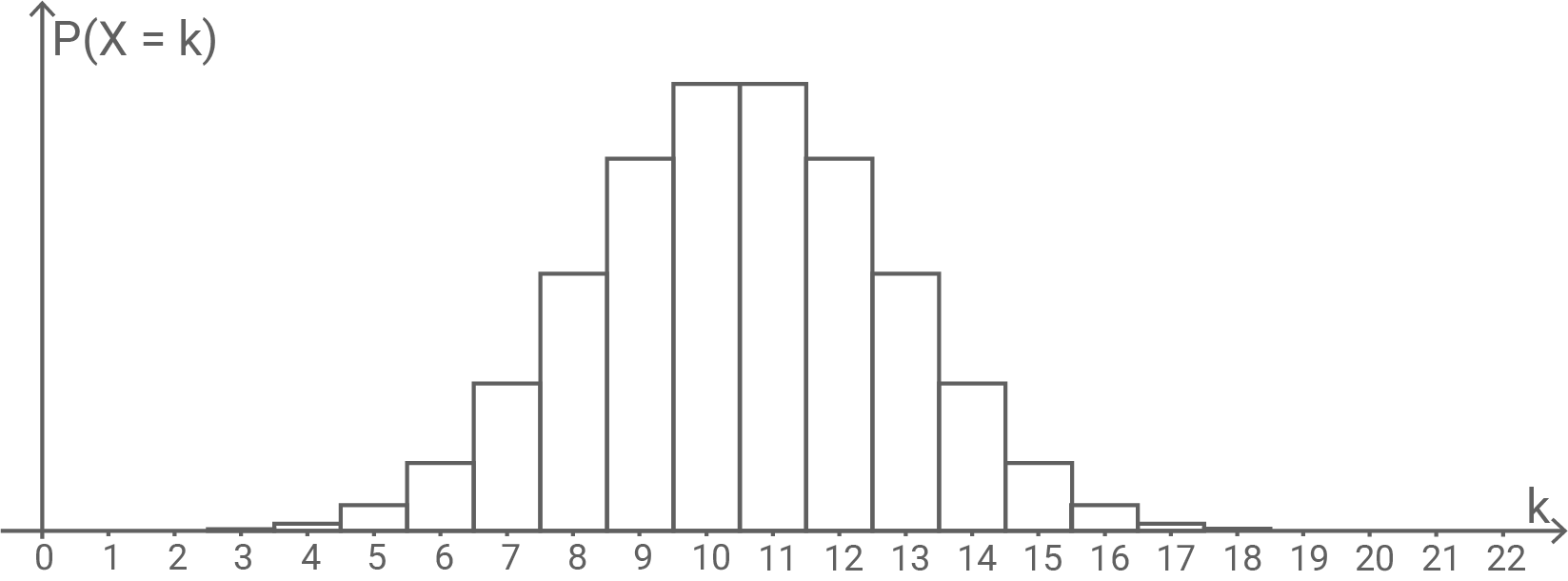
Histogramm, das die Wahrscheinlichkeitsverteilung von k darstellt, mit Werten auf der x- und y-Achse.

9.1

Es gilt $P(X=10)=P(X=11).$ Begründe, dass $n$ nicht gerade ist.

(2 BE)

9.2

Es gilt $P(X\geq9)\approx0,81$ und $P(X=12)\approx0,14.$
Berechne unter Verwendung dieser Werte näherungsweise die Wahrscheinlichkeit $P(X=10).$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

4 Analysis

4.1

Die Gleichung der Tangente $t$ kann in der Form $t(x)=mx+b$ beschrieben werden. Die Steigung $m$ lässt sich über die Ableitung der Funktion $f$ bestimmen:

$\(\begin{array}[t]{rlll} f$

Einsetzen von $x=4$ ergibt:

$\(\begin{array}[t]{rlll} m&=&f$

Der $y$ -Achsenabschnitt $b$ kann bestimmt werden, indem die Tangentengleichung dem Funktionswert von $f$ bei $x=4,$ d. h. der $y$ -Koordinate von $P(4\mid1)$ gleichgesetzt wird:

$\begin{array}[t]{rlll} y&=&mx+b &\mid\;-mx \\[5pt] y-mx&=&b \\[5pt] 1-3\cdot4&=&b \\[5pt] -11&=&b \end{array}$

Somit folgt für die Gleichung der Tangente $t(x)=3x-11.$

4.2

Graph mit einer grünen Linie und einer schwarzen Kurve im Koordinatensystem. Punkt P ist markiert.

5 Analytische Geometrie

5.1

Der Ortsvektor $\(\overrightarrow{OP$ des gespiegelten Punktes $\(P$ lässt sich mithilfe des Ortsvektors $\overrightarrow{OQ}$ und des Vektors $\overrightarrow{PQ}$ zwischen beiden Punkten bestimmen:

$\(\begin{array}[t]{rlll} \overrightarrow{OP$

Somit lauten die Koordinaten des an $Q$ gespiegelten Punktes $\(P$

5.2

Nachweisen der Lage von $\boldsymbol{Q}$ in $\boldsymbol{E}$
Einsetzen der Koordinaten von $Q$ in die Ebenengleichung von $E:\;x+3y+z=20$ liefert:

$\begin{array}[t]{rlll} x+3y+z&=&20 \\[5pt] 2+3\cdot5+3&=&20 \\[5pt] 20&=&20 \end{array}$

Somit liegt $Q$ in $E.$

Nachweisen des Normalenvektors $\boldsymbol{\overrightarrow{PQ}}$ von $\boldsymbol{E}$
Anhand der Ebenengleichung $E:\;x+3y+z=20$ lässt sich der Normalenvektor $\overrightarrow{n}$ von $E$ ablesen:

$\overrightarrow{n}=\pmatrix{1\\3\\1}$

Für $\overrightarrow{PQ}$ folgt:

$\begin{array}[t]{rlll} \overrightarrow{PQ}=\pmatrix{2-0\\5-(-1)\\3-1}&=&\pmatrix{2\\6\\2} \\[5pt] &=&2\cdot\pmatrix{1\\3\\1} \\[5pt] &=&2\cdot\overrightarrow{n} \end{array}$

Da der Vektor $\overrightarrow{PQ}$ kollinear zum Normalenvektor $\overrightarrow{n}$ ist, handelt es sich hierbei ebenfalls um einen Normalenvektor von $E.$

6 Stochastik

6.1

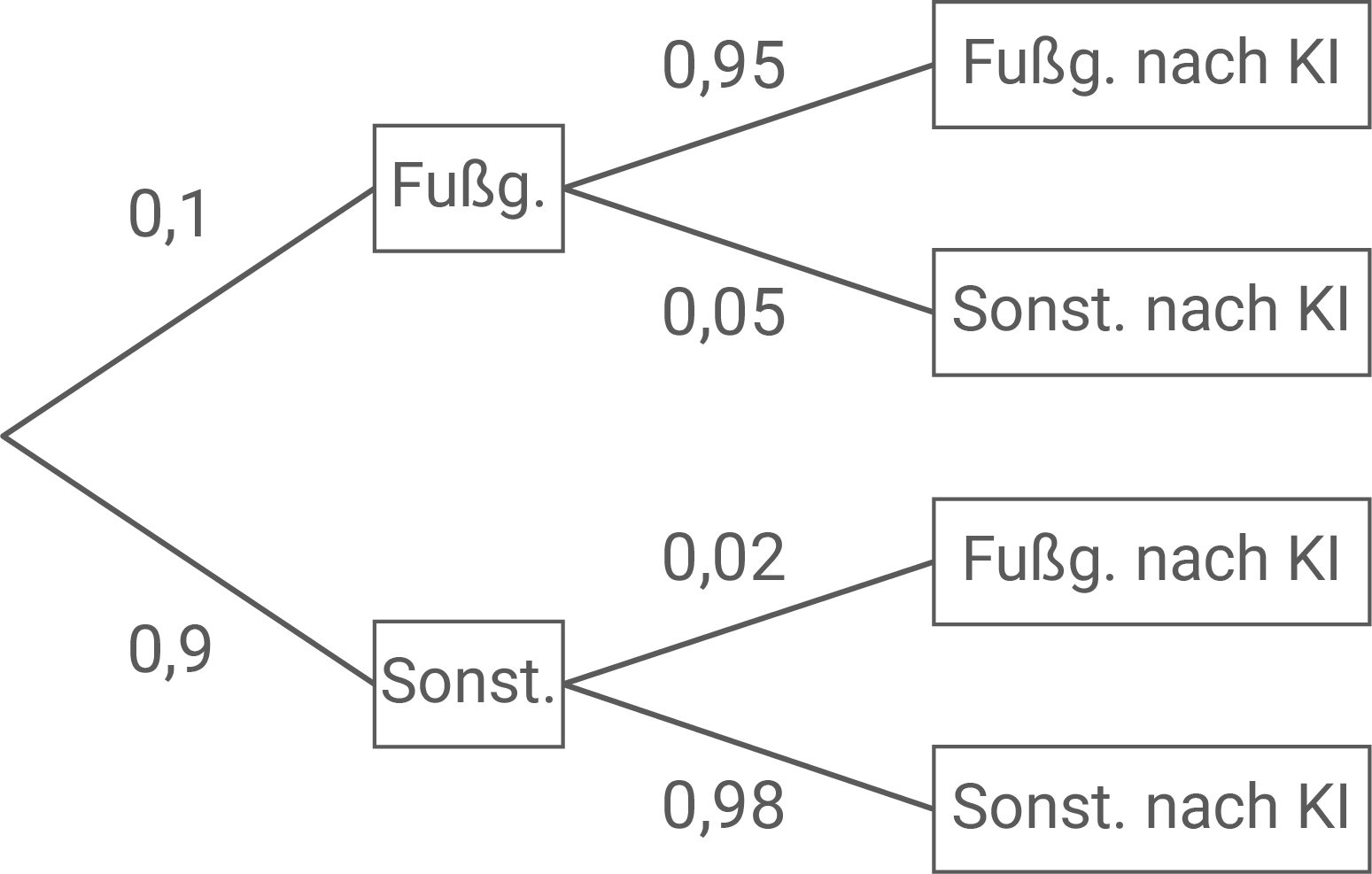
Diagramm mit Wahrscheinlichkeiten für verschiedene Ereignisse, dargestellt in einer Baumstruktur.

6.2

Der Term beschreibt die Wahrscheinlichkeit, dass ein Verkehrsteilnehmer, der von der KI als Fußgänger kategorisiert wurde, tatsächlich ein Fußgänger ist.

7 Analysis

7.1

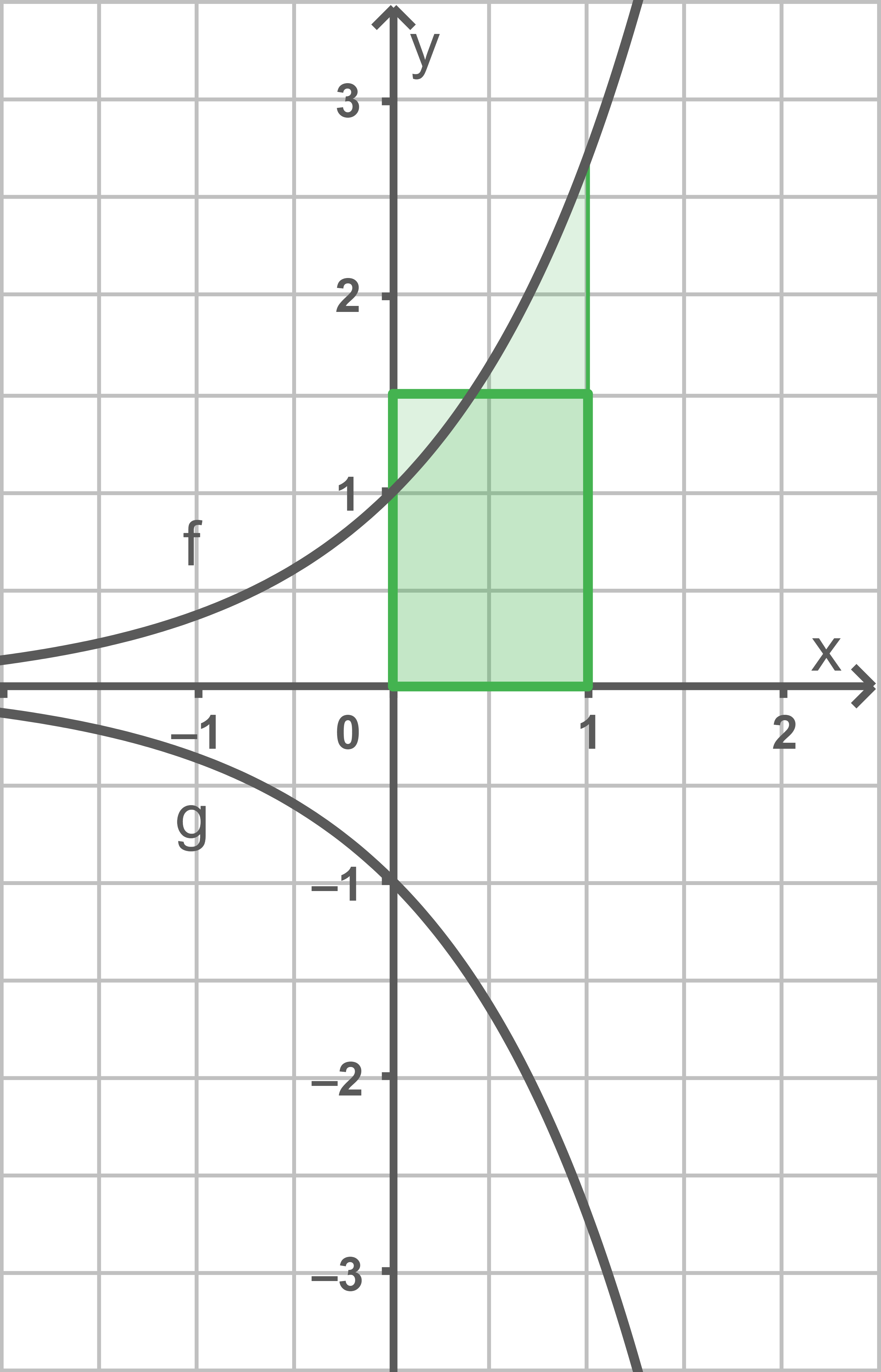
Graph mit zwei Funktionen und einem hervorgehobenen Rechteck im positiven Bereich der x-Achse.

Das gekennzeichnete Rechteck hat einen Flächeninhalt von $1,5,$ denn seine Seitenlängen betragen $1$ und $1,5.$ Ein Teil der Fläche des Rechtecks wird vom Graphen von $f$ abgeschnitten, jedoch ist der Teil der Fläche unterhalb des Graphen von $f,$ der über das Rechteck hinausragt, größer. Somit muss die Fläche unterhalb des Graphen von $f$ von $0$ bis $1$ größer als $1,5$ sein.

Alternativ können auch die Kästchen zwischen dem Graphen von $f$ und der $x$ -Achse im Intervall $[0;1]$ gezählt werden. Dies ergibt etwa $7$ Kästchen, deren Fläche je $0,25$ beträgt. Dementsprechend gilt:

$7\cdot0,25=1,75\gt1,5$

7.2

Da es sich bei $f$ und $g$ um $\mathrm{e}$ -Funktionen handelt, gilt:

$\(f(a)=f$ und $\(g(a)=g$

Für zwei senkrecht zueinander stehende Geraden muss das Produkt ihrer Steigungen $-1$ ergeben:

$m_1\cdot m_2=-1$ bzw. $m_1=-\dfrac{1}{m_2}$

Daraus folgt für die beiden Tangenten $t_f$ und $t_g:$

$\begin{array}[t]{rlll} m_{t_f}\cdot m_{t_g}&=&-1 \\[5pt] \mathrm{e}^a\cdot(-\mathrm{e}^a)&=&-1 \\[5pt] -(\mathrm{e}^a)^2&=&-1 &\mid\;\cdot\;(-1) \\[5pt] \mathrm{e}^{2a}&=&1 &\mid\;\mathrm{ln}() \\[5pt] 2a&=&\mathrm{ln}(1) &\mid\;:2 \\[5pt] a&=&0 \end{array}$

An der Stelle $a=0$ bilden die Tangenten $t_f$ und $t_g$ somit einen rechten Winkel.

8 Analytische Geometrie

8.1

Der Mittelpunkt der Grundfläche der Pyramide hat die Koordinaten $M(0\mid0\mid5).$ Somit ist $z=5$ die Gleichung der Ebene, in der die Grundfläche liegt.

8.2

Zunächst müssen die Koordinaten des Punktes $B$ ermittelt werden. Der Punkt $P$ liegt auf der Seitenkante $\overline{BS}$ der Pyramide. Der Ortsvektor von $B$ lässt sich somit folgendermaßen berechnen:

$\overrightarrow{OB}=\overrightarrow{OS}+r\cdot\overrightarrow{SP}$

Die Spitze $S$ liegt im Koordinatenursprung. Der Punkt $P$ hat die Koordinaten $P(2\mid-2\mid4)$ und die $z$ -Koordinate von $B$ beträgt $5.$ Somit ergibt sich:

$\pmatrix{x\\y\\5}=\pmatrix{0\\0\\0}+r\cdot\pmatrix{2\\-2\\4}$

Anhand der $z$ -Koordinate kann abgelesen werden, dass $r=\tfrac{5}{4}$ ist. Damit können nun die Werte von $x$ und $y$ ermittelt werden:

$x=2,5;\;y=-2,5$

Die Grundfläche $ABCD$ ist ein Quadrat. Der Flächeninhalt $A$ wird durch das Quadrat der Länge einer der Seitenkanten berechnet. Die $x$ -Koordinate von $B$ ist lediglich die Hälfte der Länge einer Seitenkante, somit folgt für den Flächeninhalt:

$A=(2x)^2=5^2=25$

9 Stochastik

9.1

Da es sich um eine Binomialverteilung handelt, gilt für den Erwartungswert:

$E(X)=n\cdot p=n\cdot0,5$

Die Wahrscheinlichkeitsverteilung von $X$ nimmt sowohl bei $k=10$ als auch bei $k=11$ ihren größten Wert an. Demnach ist der Erwartungswert nicht ganzzahlig und $n$ folglich nicht gerade.

9.2

Die Wahrscheinlichkeitsverteilung ist symmetrisch, somit gilt:

$P(X=9)=P(X=12)\approx0,14$ und $P(X\geq11)=0,5$

Somit folgt:

$\begin{array}[t]{rlll} P(X=10)&=&P(X\geq9)-P(X=9)-P(X\geq11) \\[5pt] &\approx&0,81-0,14-0,5 \\[5pt] &=&0,17 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?