4 Stochastik – Wahlaufgabe

In den beiden benachbarten Städten X-Stadt und Y-Stadt werden monatlich erscheinende Zeitungen verteilt.

4.1

Erfahrungsgemäß werden in X-Stadt $10\,\%$ der Zeitungen nicht gelesen. In einer Straße dieser Stadt werden $25$ Zeitungen verteilt. Die Zufallsgröße $X$ gibt dabei die Anzahl der nicht gelesenen Zeitungen an und wird als binomialverteilt angenommen.

4.1.1

Berechne den Wert von $P(X=2)$ und gib die Bedeutung dieses Terms im Sachzusammenhang an.

(2 BE)

4.1.2

Ermittle die Wahrscheinlichkeit für das Ereignis: „Die Anzahl der nicht gelesenen Zeitungen beträgt mindestens eins, aber weniger als fünf.“

(2 BE)

4.2

Die Anzahl der Zeitungen, die in einer vergleichbaren Straße in Y-Stadt nicht gelesen werden, wird durch die binomialverteilte Zufallsgröße $Y$ beschrieben. Die Abbildung 1 zeigt die Wahrscheinlichkeitsverteilung von $Y$ für $n=25.$

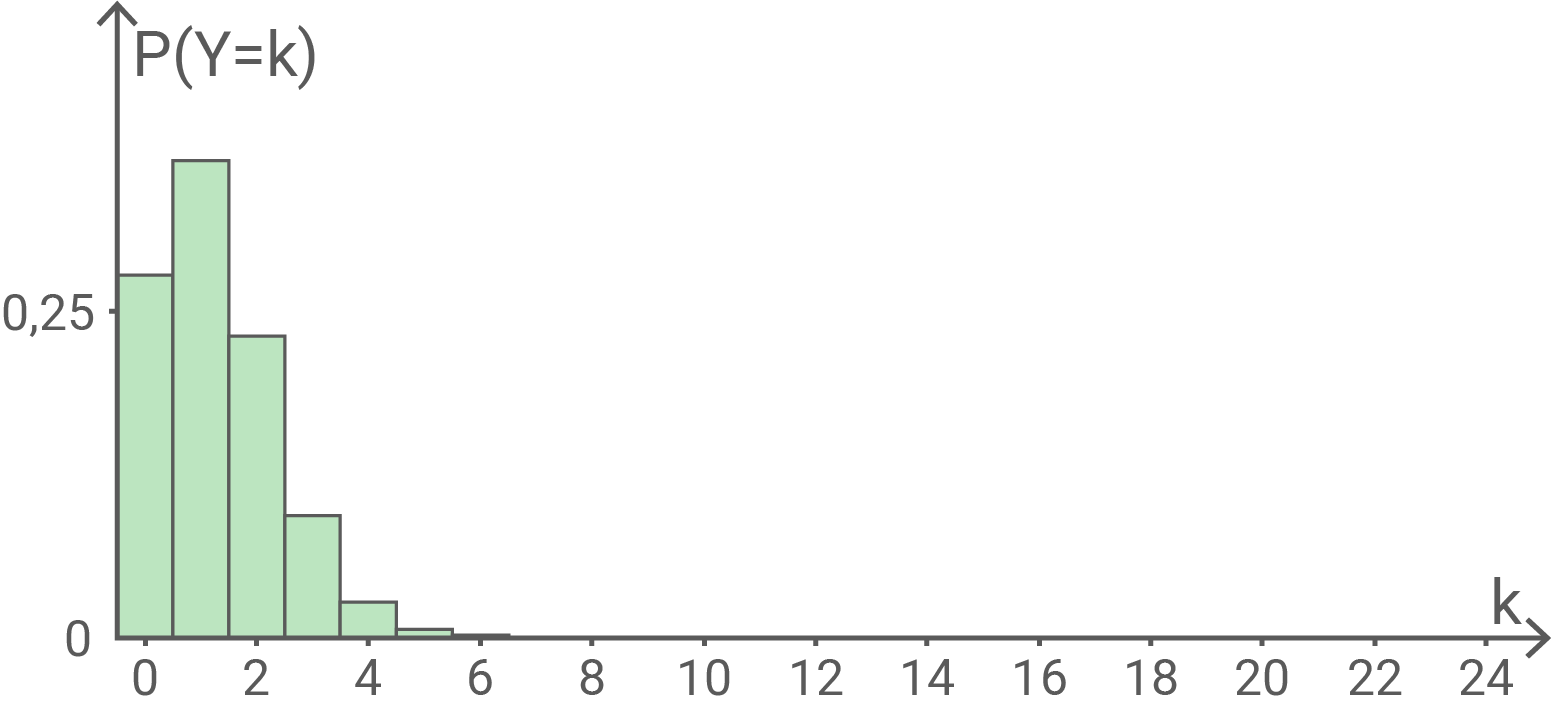
Balkendiagramm mit Wahrscheinlichkeitsverteilung P(Y=k) in Abhängigkeit von k.

Abbildung 1

Beurteile für Y-Stadt mithilfe der Abbildung 1 die folgenden Aussagen:

Die Wahrscheinlichkeit dafür, dass von den $25$ Zeitungen weniger als zwei nicht gelesen werden, ist größer als $50\,\%.$
Es ist zu erwarten, dass der Anteil der nicht gelesenen Zeitungen $8\,\%$ beträgt.

(4 BE)

4.3

In $40\,\%$ der Haushalte von X-Stadt leben Kinder. Es wird ein Haushalt in dieser Stadt zufällig ausgewählt. Dazu werden folgende Ereignisse betrachtet:

$K:$	In dem ausgewählten Haushalt leben Kinder.
$L:$	In dem Haushalt wird die Zeitung gelesen.

4.3.1

Vervollständige für diesen Sachverhalt die Vierfeldertafel in der Abbildung 2.

	$\color{#FFFFFF}{\overline{K}}$
$\color{#FFFFFF}{L}$	$0,55$	$0,9$
$\color{#FFFFFF}{\overline{L}}$
		$1$

Abbildung 2

Gib den Anteil derjenigen Haushalte in X-Stadt an, in denen keine Kinder leben und die Zeitung nicht gelesen wird.

(3 BE)

4.3.2

Der Zeitung wird eine neue Rubrik für Kinder hinzugefügt. Unter den Haushalten mit Kindern in X-Stadt erhöht sich dadurch der Anteil derjenigen Haushalte, in denen die Zeitung gelesen wird, auf $90\,\%.$ Auf das Leseverhalten in den Haushalten ohne Kinder hat diese Veränderung keinen Einfluss.

Bestimme den Anteil aller Haushalte in X-Stadt, in denen die Zeitung jetzt gelesen wird.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

4.1

4.1.1

Berechnung des Werts von $\boldsymbol{P(X=2)}$
Es handelt sich um eine Binomialverteilung. Für $X=2$ mit $n=25$ und $p=0,10$ ergibt sich somit:

$\begin{array}[t]{rlll} P(X=2)&=&\pmatrix{25\\2}\cdot0,10^2\cdot(1-0,10)^{25-2} \\[5pt] &\approx&0,27 \\[5pt] &\approx&27\,\% \end{array}$

Bedeutung im Sachzusammenhang angeben
Der Term gibt die Wahrscheinlichkeit dafür an, dass in der Straße zwei Zeitungen nicht gelesen werden.

4.1.2

$\begin{array}[t]{rlll} P(1\leq X\leq4)&=&P(X\leq4)-P(X=0) \\[5pt] &\approx&0,902-0,072 \\[5pt] &\approx&0,83 \\[5pt] &\approx&83\,\% \end{array}$

4.2

Aussage 1 ist wahr, da der Anteil des Flächeninhalts der ersten beiden Säulen für $k=0$ und $k=1$ zusammen größer als $50\,\%$ des Flächeninhalts aller dargestellten Säulen ist.

Aussage 2 ist falsch. Bei einer Binomialverteilung gilt $E(X)=n\cdot p,$ somit müsste für $p=0,08$ der Erwartungswert $E(X)=25\cdot0,08=2$ betragen und damit die Säule für $k=2$ die höchste sein.

4.3

4.3.1

	$\color{#FFFFFF}{K}$	$\color{#FFFFFF}{\overline{K}}$
$\color{#FFFFFF}{L}$	$0,35$	$0,55$	$0,9$
$\color{#FFFFFF}{\overline{L}}$	$0,05$	$0,05$	$0,1$
	$0,4$	$0,6$	$1$

Für den Anteil der Haushalte, in denen keine Kinder leben und keine Zeitung gelesen wird, gilt:

$P(\overline{K}\cap\overline{L})=0,05$

4.3.2

	$\color{#FFFFFF}{K}$	$\color{#FFFFFF}{\overline{K}}$
$\color{#FFFFFF}{L}$		$0,55$	$a$
$\color{#FFFFFF}{\overline{L}}$		$0,05$
	$0,4$	$0,6$	$1$

Unter den Haushalten mit Kindern erhöht sich der Anteil, in denen Zeitung gelesen wird, auf $90\,\%.$ Folglich gilt:

$\begin{array}[t]{rlll} P_K(L)&=&\dfrac{P(K\cap L)}{P(K)} \\[5pt] 0,9&=&\dfrac{P(K\cap L)}{0,4} &\mid\;\cdot\;0,4 \\[5pt] 0,36&=&P(K\cap L) \end{array}$

Somit gilt für $a:$

$a=0,36+0,55=0,91$

Der Anteil aller Zeitung lesenden Haushalte beträgt nun $91\,\%.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?