Analysis
1
Gegeben sind die Funktion  und ihre erste Ableitungsfunktion
und ihre erste Ableitungsfunktion  mit den Gleichungen
mit den Gleichungen  und
und  sowie
sowie  Der Graph von
Der Graph von  ist
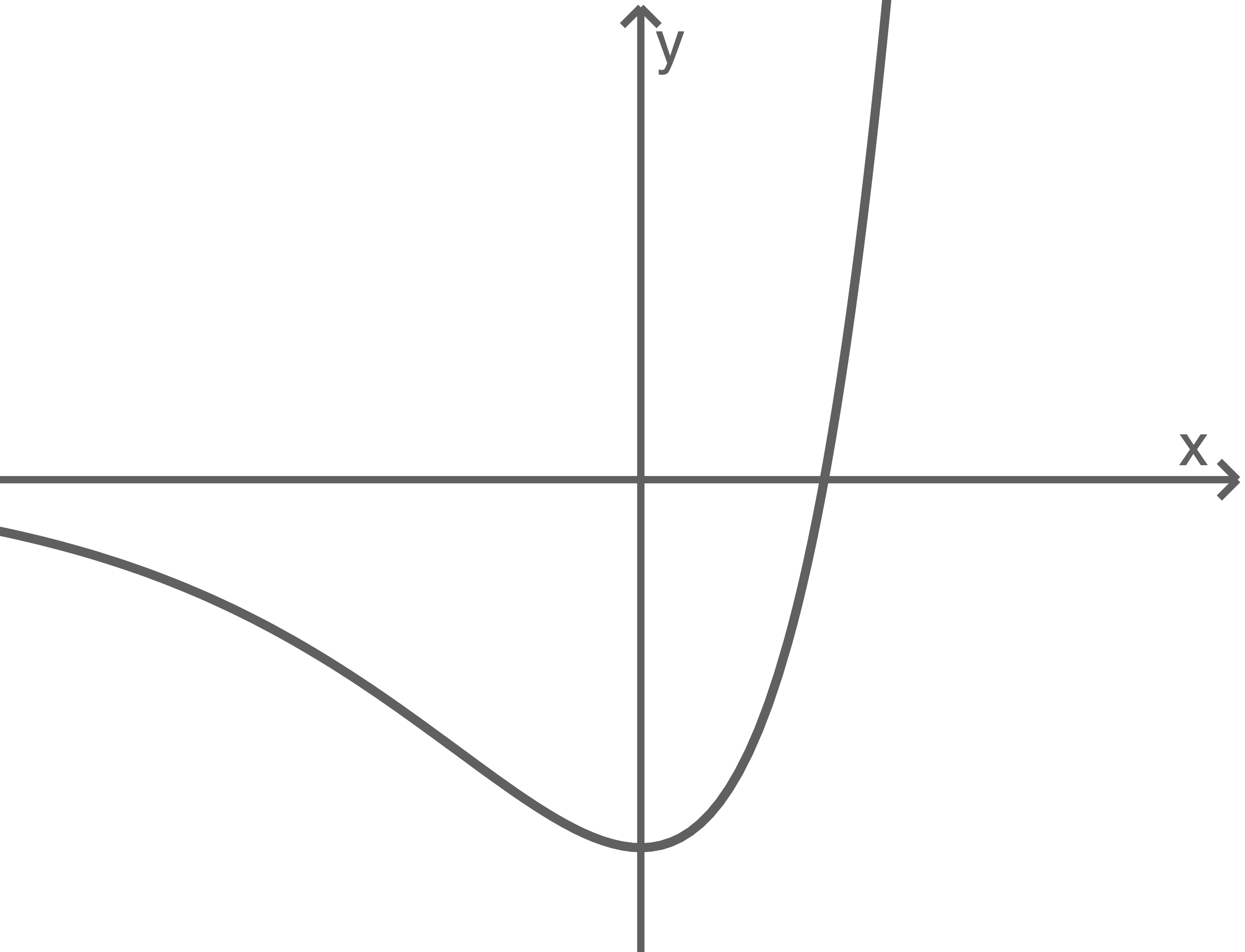
ist  dieser ist in der Abbildung dargestellt.
dieser ist in der Abbildung dargestellt.
1.1
Zeige, dass  die Nullstelle von
die Nullstelle von  ist.
ist.
(1 BE)
1.2
Bestimme die Koordinaten dieses Tiefpunkts.
(2 BE)
1.3
Im Wendepunkt  wird die Tangente
wird die Tangente  an
an  gelegt.
gelegt.
Ermittle rechnerisch eine Gleichung von
Ermittle rechnerisch eine Gleichung von
(3 BE)
1.4
Berechne den Inhalt der Fläche, die im vierten Quadranten durch
(2 BE)
1.5
Betrachtet werden die Funktionen  Jeder Graph von
Jeder Graph von  verläuft durch den Punkt
verläuft durch den Punkt 
Begründe, dass für alle negativen Werte von der Graph von
der Graph von  jeweils nur einen Punkt mit
jeweils nur einen Punkt mit  gemeinsam hat.
gemeinsam hat.
Begründe, dass für alle negativen Werte von
(2 BE)
2
Gegeben ist eine Funktion  durch die Gleichung
durch die Gleichung  mit
mit 
Der Graph von ist
ist 
Der Graph von
2.1
Zeige, dass die Funktion  nur die Nullstelle
nur die Nullstelle  hat.
hat.
Berechne die Koordinaten der Extrem- und der Wendepunkte von
Weise die Art der Extrema nach.
Berechne die Koordinaten der Extrem- und der Wendepunkte von
Weise die Art der Extrema nach.
(8 BE)
2.2
Im Punkt  wird die Tangente
wird die Tangente  an
an  gelegt.
gelegt.
Berechne die Größe des Winkels, unter dem die
die  -Achse schneidet.
-Achse schneidet.
Begründe, dass eine zu parallele Tangente an
parallele Tangente an  existiert.
existiert.
Berechne die Größe des Winkels, unter dem
Begründe, dass eine zu
(4 BE)
2.3
Der Graph  die
die  -Achse und die Gerade
-Achse und die Gerade  schließen eine Fläche vollständig ein.
schließen eine Fläche vollständig ein.
Berechne den Inhalt dieser Fläche.
Berechne den Inhalt dieser Fläche.
(3 BE)
2.4
Die Kosten, die einer Firma bei der Herstellung einer Flüssigkeit entstehen, können durch die Kostenfunktion  mit
mit  für
für  beschrieben werden. Die Funktionsterme von
beschrieben werden. Die Funktionsterme von  und
und  sind gleich.
sind gleich.
Dabei gibt die Kosten in Euro an, die bei der Produktion von
die Kosten in Euro an, die bei der Produktion von  Litern der Flüssigkeit insgesamt entstehen. Die Funktion
Litern der Flüssigkeit insgesamt entstehen. Die Funktion  mit
mit  gibt für
gibt für  und
und  den Erlös beim Verkauf von
den Erlös beim Verkauf von  Litern in Euro an. Für die Gewinnfunktion gilt
Litern in Euro an. Für die Gewinnfunktion gilt 
Dabei gibt
2.4.1
Zeichne die Graphen von  und
und  im Intervall
im Intervall  in ein Koordinatensystem.
in ein Koordinatensystem.
(4 BE)
2.4.2
Beschreibe die gegenseitige Lage der Graphen von  und
und  in diesem Intervall. Leite die entsprechende Schlussfolgerungen hinsichtlich des erzielten Gewinns ab.
in diesem Intervall. Leite die entsprechende Schlussfolgerungen hinsichtlich des erzielten Gewinns ab.
(4 BE)
2.4.3
Berechne für  den Wert von
den Wert von  , für den ein maximaler Gewinn erzielt wird.
, für den ein maximaler Gewinn erzielt wird.
(5 BE)
2.4.4
Interpretiere den Wert von  im Sachzusammenhang.
im Sachzusammenhang.
(3 BE)
2.4.5
Es gibt einen kleinsten Wert von  so, dass der Verkauf einer Flüssigkeitsmenge gerade noch verlustfrei erfolgen kann.
so, dass der Verkauf einer Flüssigkeitsmenge gerade noch verlustfrei erfolgen kann.
Zeichne den Graphen dieser Funktion ein.
ein.
Bestimme mithilfe dieser grafischen Darstellung den Wert von
Zeichne den Graphen dieser Funktion
Bestimme mithilfe dieser grafischen Darstellung den Wert von
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1.2
Notwendige Bedingung:
 also
also  und somit
und somit  Hinreichende Bedingung:
Hinreichende Bedingung:



 also folgt daraus, dass ein Tiefpunkt vorliegen muss.
Koordinaten berechnen:
also folgt daraus, dass ein Tiefpunkt vorliegen muss.
Koordinaten berechnen: 


1.3
1.4
1.5
Für negative Werte von  verlaufen alle Graphen von
verlaufen alle Graphen von  monoton fallend durch den Punkt
monoton fallend durch den Punkt  und somit für
und somit für  oberhalb und für
oberhalb und für  unterhalb der
unterhalb der  -Achse.
-Achse.
 hingegen mit nur einer Nullstelle bei
hingegen mit nur einer Nullstelle bei  verläuft für kleinere Werte als
verläuft für kleinere Werte als  unterhalb und für größere Werte von
unterhalb und für größere Werte von  oberhalb der
oberhalb der  -Achse. Es kann also keine weiteren Schnittpunkte geben.
-Achse. Es kann also keine weiteren Schnittpunkte geben.
2.1
Zeigen, dass  nur eine Nullstelle hat
nur eine Nullstelle hat



 Der zweite Faktor mit
Der zweite Faktor mit  multipliziert ergibt:
multipliziert ergibt:

![\(\begin{array}[t]{rll}
x_{2,3}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-15}{2} \pm \sqrt{\left(\dfrac{-15}{2}\right)^2-72}
\\[5pt]
&=& 7,5 \pm \sqrt{-15,75}
\end{array}\)](https://www.schullv.de/resources/formulas/3333a86c383e8f2bfd57fdd90f8ca3724c3a816a9b55c2fd4395d3a7a30e14a3_light.svg) Die quadratische Gleichung hat keine Lösung.
Koordinaten der Extrem- und Wendepunkte berechnen
Die quadratische Gleichung hat keine Lösung.
Koordinaten der Extrem- und Wendepunkte berechnen
Extrempunkte

 Notwendige Bedingung:
Notwendige Bedingung:


![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-10}{2} \pm \sqrt{\left(\dfrac{-10}{2}\right)^2-24}\\[5pt]
x_{1,2}&=& 5 \pm \sqrt{25-24}
\end{array}\)](https://www.schullv.de/resources/formulas/df859eac98e30c0ecbf4e91af4da77ec8ac6c0b71e48916e597ffb847b058f3f_light.svg)

 Hinreichende Bedingung:
Hinreichende Bedingung:
 also liegt hier ein lokales Minimum vor
also liegt hier ein lokales Minimum vor
 also liegt hier ein lokales Maximum vor
also liegt hier ein lokales Maximum vor



 Wendepunkt(e)
Notwendige Bedingung:
Wendepunkt(e)
Notwendige Bedingung:

 also
also  Hinreichende Bedingung:
Hinreichende Bedingung:





Extrempunkte
2.2
Größe des Winkels berechnen
Steigung im Punkt  berechnen:
berechnen: 

 daraus folgt
daraus folgt  Begründen, dass eine zu
Begründen, dass eine zu  parallele Tangente existiert
Der Graph der Ableitungsfunktion ist eine Parabel, d.h. jeder Funktionswert außer dem des Scheitelpunkts bei
parallele Tangente existiert
Der Graph der Ableitungsfunktion ist eine Parabel, d.h. jeder Funktionswert außer dem des Scheitelpunkts bei  tritt zweimal auf.
tritt zweimal auf.
Da gibt es einen weiteren Punkt auf
gibt es einen weiteren Punkt auf  an dem eine Tangente parallel zu
an dem eine Tangente parallel zu  verläuft.
verläuft.
Da
2.3
2.4.1
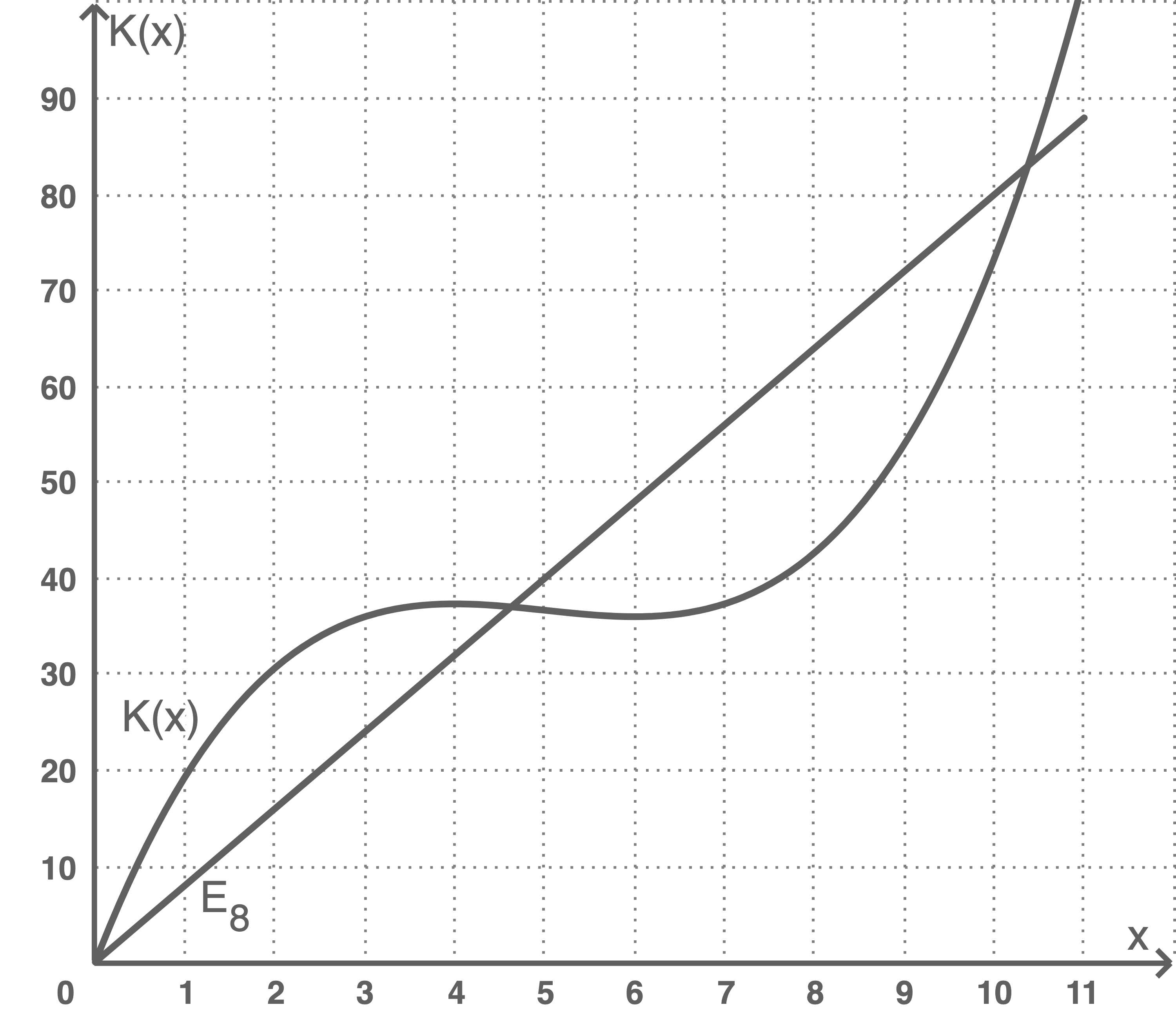
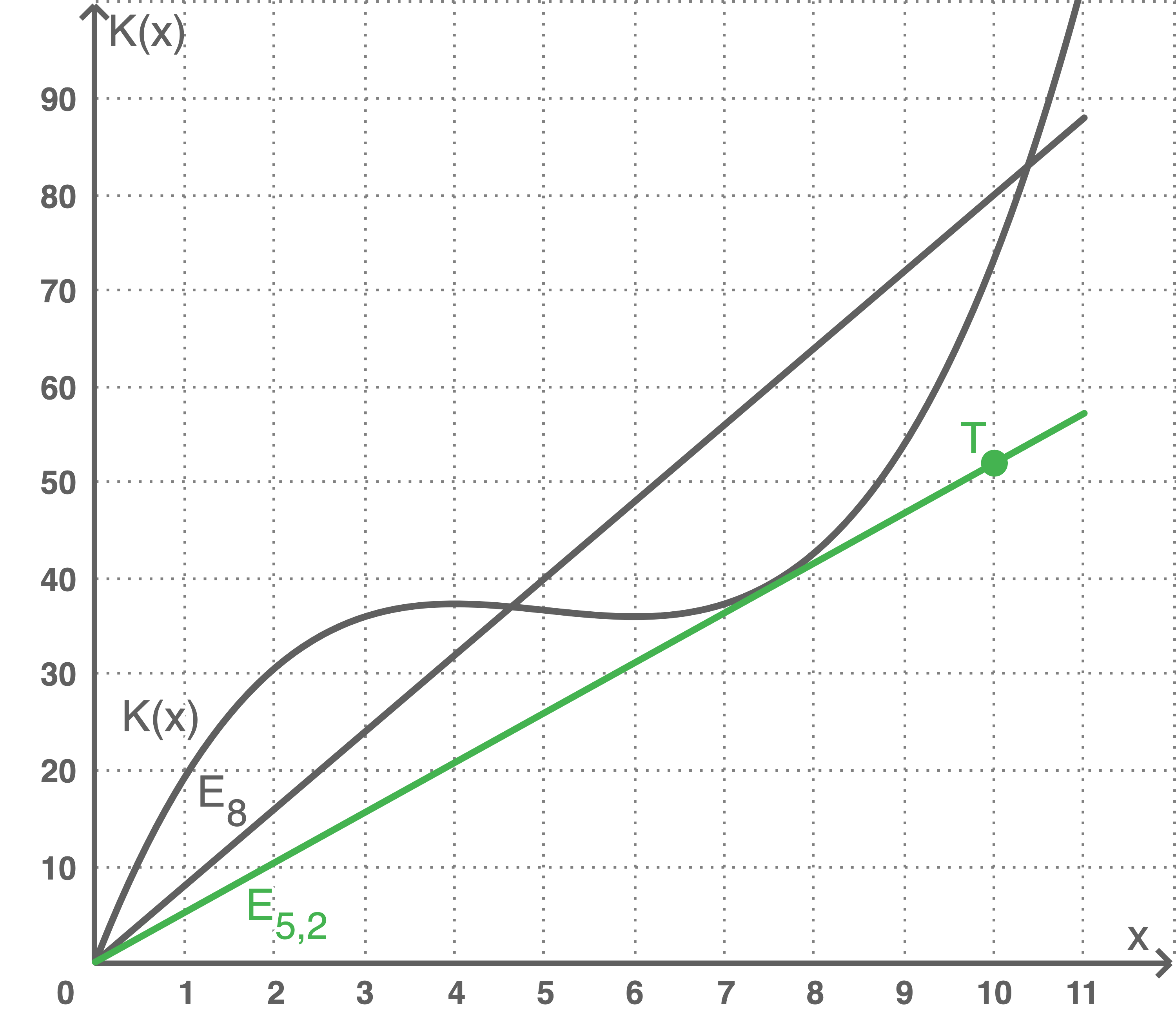
2.4.2
Die Graphen schneiden sich im Koordinatenursprung, dann bei 4,6 und nochmal bei 10,4. Zwischen dem Koordinatenursprung und der Stelle 4,6 verläuft der Graph von  oberhalb von
oberhalb von  zwischen der Stelle 4,6 und 10,4 unterhalb von
zwischen der Stelle 4,6 und 10,4 unterhalb von  .
Dsa Unternehmen erzielt Gewinn, wenn mehr als 4,6 bzw. weniger als 10,4 Liter Flüssigkeit hergestellt und verkauft werden.
.
Dsa Unternehmen erzielt Gewinn, wenn mehr als 4,6 bzw. weniger als 10,4 Liter Flüssigkeit hergestellt und verkauft werden.
2.4.3
2.4.4
2.4.5