1 Analysis – Pflichtaufgabe

Gegeben ist die Funktionenschar $f_a$ mit $f_a(x)=\dfrac{3}{100} \cdot x^3-\dfrac{91}{100} \cdot x^2+a \cdot x-26$ für $a, x \in \mathbb{R}.$

1.1

Gib für die Graphen der Schar $f_a$ den Schnittpunkt mit der $y$ -Achse sowie das Verhalten für $x \rightarrow-\infty$ und für $x \rightarrow+\infty$ an.

(3 BE)

1.2

Berechne die Koordinaten der Wendepunkte der Schar und gib die Form der Ortskurve der Wendepunkte an.

(4 BE)

1.3

Für alle Graphen der Schar gilt folgende Aussage:

Wenn der Anstieg der Tangente im Wendepunkt negativ ist, dann besitzt der Graph lokale Extrempunkte.

Begründe diese Aussage.

(3 BE)

Beim Laufen bildet sich im menschlichen Körper Laktat (Milchsäure). Die Laktatkonzentration ist abhängig von der Belastung der Muskeln. Die Messung der Laktatkonzentration im Blut dient zur Diagnostik der Ausdauerleistung und zur Trainingsplanung. Ein Ziel der Diagnostik ist dabei die Bestimmung der Laktatschwelle. Vereinfacht bezeichnet diese die höchste Laufgeschwindigkeit, die langfristig durchgehalten werden kann, z. B. bei einem Marathon.

Für eine Läuferin kann auf Grundlage ihrer Messwerte die Laktatkonzentration $k$ durch die Funktion $k(x)=\dfrac{3}{100} x^3-\dfrac{91}{100} x^2+9 x-26$ mit $7 \leq x \leq 18$ modelliert werden.

Dabei ist $x$ die Laufgeschwindigkeit in $\text{km/h}$ (Kilometer pro Stunde) und $k(x)$ die Laktatkonzentration in $\text{mmol/L}$ (Millimol pro Liter).

Den in Abbildung 1 dargestellten Graphen von $k$ nennt man Laktatkurve der Läuferin.

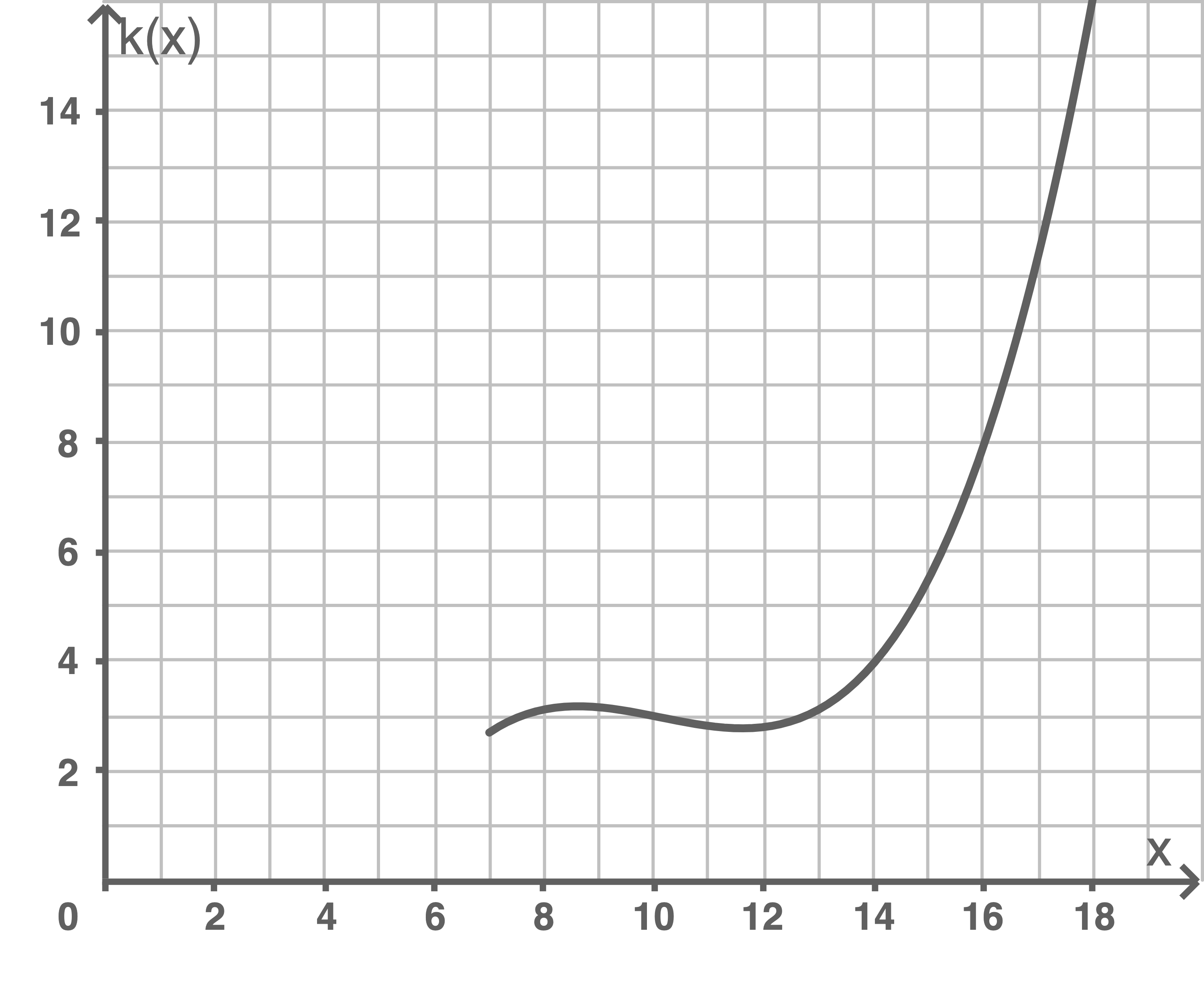
Graf eines mathematischen Funktionsverlaufs mit x- und y-Achse, gekennzeichnet als k(x).

Abbildung 1

1.4

Zur Ermittlung der individuellen Laktatschwelle existieren in der Sportmedizin verschiedene mathematische Methoden:

1.4.1

Mader-Methode: Bei Erreichung von genau $4\;\text{mmol}$ Laktat pro Liter Blut.
Simon-Methode: Der Steigungswinkel der Laktatkurve erreicht die Größe $45^{\circ}.$

Berechne und vergleiche für die Läuferin für beide Methoden die Laktatschwelle.

(5 BE)

1.4.2

Eine weitere Methode verwendet zur Bestimmung der Laktatschwelle den Punkt der Laktatkurve mit der maximalen orthogonalen Entfernung zur Sekante, welche die Laktatwerte zu Beginn und Ende des Messintervalls $7 \leq x \leq 18$ verbindet.

Fertige dazu unter Verwendung der Abbildung 1 eine Skizze an und berechne für die Läuferin den Wert dieser Laktatschwelle.

(5 BE)

1.5

Die Laktatproduktion im menschlichen Körper wird durch die Sauerstoffaufnahme beeinflusst.

Abbildung 2 zeigt die Sauerstoffaufnahme $s$ in $\text{L/min}$ (Liter pro Minute) in Abhängigkeit von der Zeit $t$ in $\text{min}$ (Minuten) für eine Ruhephase und für eine anschließende Laufphase.

Für die Läuferin gilt:
$RW=0,25 \;\text{L/min}$ und $SW=0,8 \;\text{L/min}$ sowie $t_1=5 \;\text{min}.$

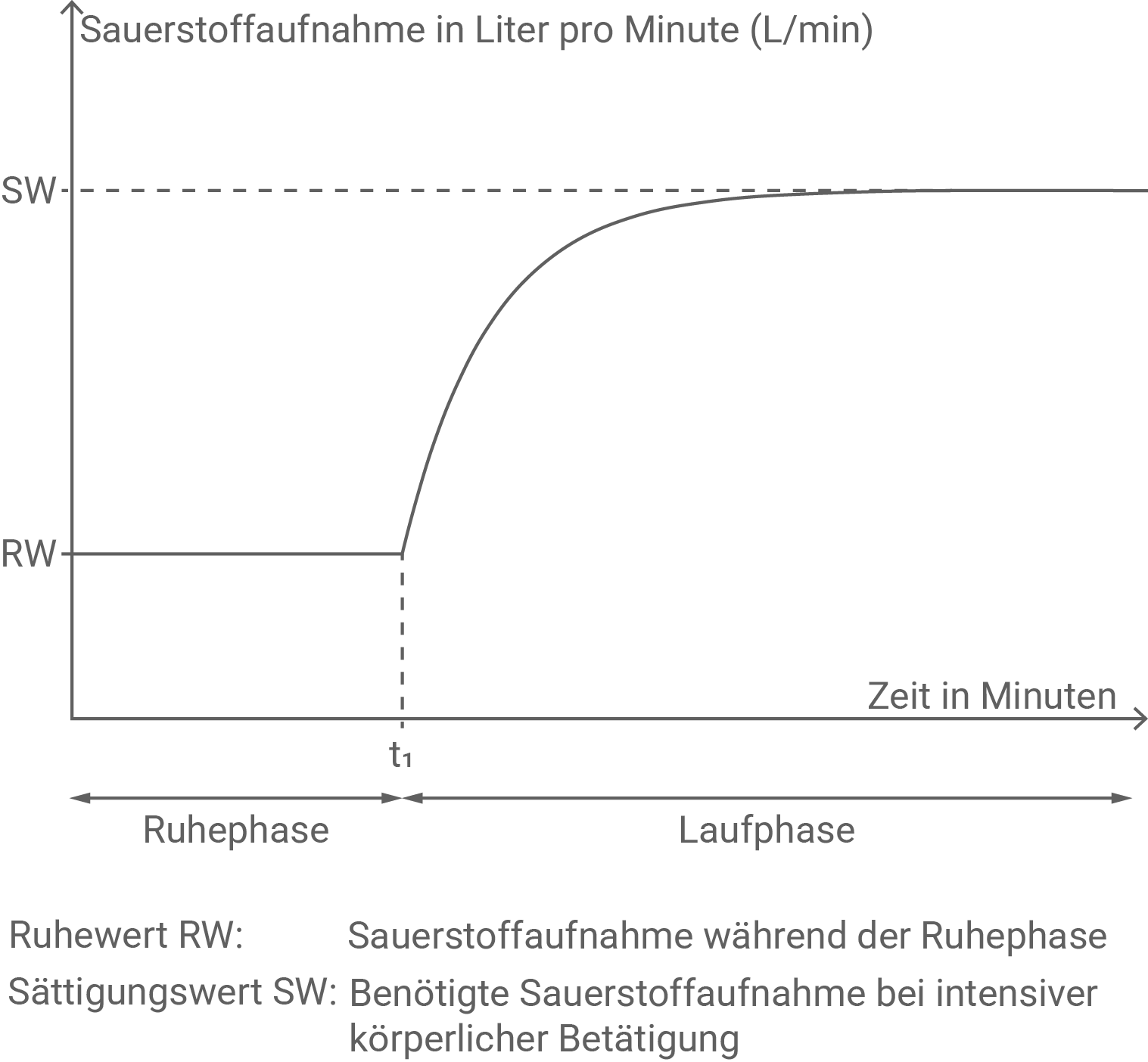
Diagramm zur Sauerstoffaufnahme in L/min über Zeit, zeigt Ruhe- und Laufphase sowie Ruhe- und Sättigungswerte.

Abbildung 2

1.5.1

Interpretiere die Gleichung $\(\lim\limits_{t\to\infty}s$ im Sachzusammenhang.

(2 BE)

1.5.2

Die Sauerstoffaufnahme während der Laufphase lässt sich mithilfe der Exponentialfunktion $s$ mit $s(t)=-23,5 \cdot \text{e}^{b \cdot t}+c$ und $t \in \mathbb{R}, t \geq t_1$ sowie reeller Werte $b\lt0, c\gt0$ modellieren. Ermittle die Werte der Parameter $b$ und $c.$

(4 BE)

1.5.3

Ein Sauerstoffdefizit entsteht, wenn die momentane Sauerstoffaufnahme geringer ist als die benötigte Sauerstoffaufnahme während der Laufphase. Dieses Defizit wird mithilfe des Terms $\displaystyle\int_{t_1}^{t_2}(S W-s(t)) \;\text{d} t$ mit $t_2\gt t_1$ bestimmt.

Berechne das Sauerstoffdefizit der Läuferin in den ersten $5$ Minuten der Laufphase und interpretiere diesen Wert im Sachzusammenhang.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\begin{array}[t]{rlll} f_a(0)&=&\dfrac{3}{100} \cdot 0^3-\dfrac{91}{100} \cdot 0^2+a \cdot 0-26 \\[5pt] &=&-26 \end{array}$

Der Schnittpunkt der Schar $f_a$ mit der $y$ -Achse hat somit die Koordinaten $S_y(0\mid-26).$

Da $f_a$ für alle $a$ eine ganzrationale Funktion mit Grad $3,$ also insbesondere ungeradem Grad, ist, gilt:

$\begin{array}[t]{rlll} \lim\limits_{x\to\infty}f_a(x)&=&\infty \\[5pt] \lim\limits_{x\to-\infty}f_a(x)&=&-\infty \end{array}$

1.2

Mit dem CAS folgt für die ersten drei Ableitungen von $f_a:$

$\(\begin{array}[t]{rlll} f_a$

Auflösen von $\(f_a$ nach $x$ mit dem solve-Befehl des CAS liefert:

$x=\dfrac{91}{9}$

Da die dritte Ableitung von $f_a$ für alle $a$ konstant ungleich Null ist, ist auch die hinreichende Bedingung für Wendestellen erfüllt und einsetzen von $x=\frac{91}{9}$ in $f_a$ liefert für die $y$ -Koordinate der Wendestelle:

Rechenweg anzeigen

$f_a\left(\dfrac{91}{9}\right) = \dfrac{91}{9}a-\dfrac{1.069.471}{12150}$

Die Wendepunkte der Schar besitzen somit die Koordinaten $W_a\left(\frac{91}{9}\mid\frac{91}{9}a-\frac{1.069.471}{12150}\right).$ Aufgrund der Struktur der $y$ -Koordinate von $W_a$ folgt, dass die Ortskurve der Wendepunkte eine Gerade ist.

1.3

Jede ganzrationale Funktion dritten Grades besitzt genau einen Wendepunkt und entweder keine oder zwei Extrempunkte. Die Funktion besitzt genau dann keine Extrempunkte, wenn der Wendepunkt ein Sattelpunkt ist.
Die Tangente in einem Sattelpunkt ist immer waagerecht, das heißt im Fall einer Tangente mit negativem Anstieg im Wendepunkt kann dieser kein Sattelpunkt sein. Somit besitzt der Graph in diesem Fall zwei Extrempunkte und die Aussage aus der Aufgabenstellung ist richtig.

1.4

1.4.1

Mader-Methode

Auflösen von $k(x)=4$ nach $x$ mit dem solve-Befehl des CAS liefert:

$x\approx14\;\frac{\text{km}}{\text{h}}$

Simon-Methode

Der Steigungswinkel einer Funktion entspricht genau dann $45^\circ,$ wenn die Steigung der Funktion an dieser Stelle $1$ beträgt. Für die erste Ableitung von $k$ folgt mit dem CAS:

$\(k$

Auflösen von $\(k$ nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1&\approx&6,5\;\frac{\text{km}}{\text{h}} \\[5pt] x_2&\approx&13,8\;\frac{\text{km}}{\text{h}} \end{array}$

Da $x_1\lt7$ gilt, ist nur $x_2$ relevant. Damit liefern die beiden Methoden näherungsweise die gleiche Laktatschwelle.

1.4.2

Wert der Laktatschwelle berechnen

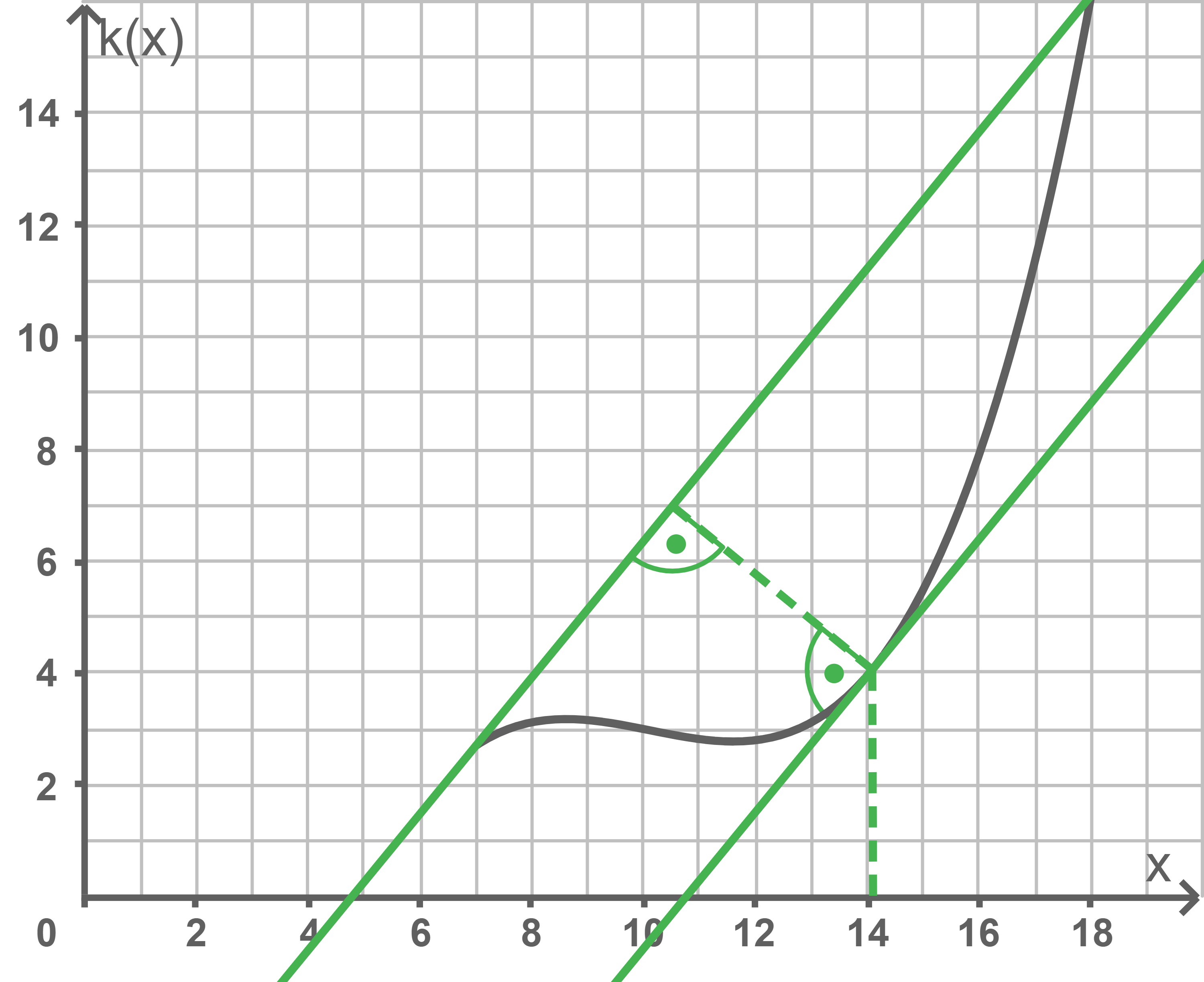
Der Punkt mit dem maximalen orthogonalen Abstand zur Sekante ist der Punkt des Graphen, an dem die Steigung der Tangente der Steigung der in der Aufgabenstellung beschriebenen Sekante entspricht. Für diese Steigung gilt:

$\dfrac{k(18)-k(7)}{18-7}=1,22$

Auflösen von $\(k$ nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1&\approx&6,1 \\[5pt] x_2&\approx&14,1 \end{array}$

Da $x_1\lt7$ gilt, folgt $x_2\approx14,1$ für die gesuchte Laktatschwelle.

Skizze anfertigen

Graph mit einer Funktion und zwei Linien, die verschiedene Punkte und Winkel anzeigen.

1.5

1.5.1

Bei zunehmender Zeit geht die Steigung der Sauerstoffaufnahme irgendwann gegen Null, d.h. die Sauerstoffaufnahme nähert sich auf lange Zeit gesehen einem Grenzwert an, der durch den Sättigungswert $SW$ gegeben ist.

1.5.2

Für $b\lt0$ gilt:

$\lim\limits_{x\to\infty}\left(-23,5 \cdot \mathrm e^{b \cdot t}\right)=0$

Da der Grenzwert von $s(t)$ somit durch $c$ gegeben ist und außerdem dem Sattigungswert entspricht, folgt damit $c=0,8.$ Mit dem Ruhewert ergibt sich außerdem $s(5)=0,25$ und dadurch mit dem solve-Befehl des CAS für $b:$

$b\approx-0,75$

1.5.3

$\displaystyle\int_{5}^{10}\left(SW-s(t)\right)\;\mathrm dt=\displaystyle\int_{5}^{10}\left(23,5 \cdot \mathrm e^{-0,75 \cdot t}\right)\;\mathrm dt$

Berechnen des Integrals mit dem CAS liefert:

$\displaystyle\int_{5}^{10}\left(SW-s(t)\right)\;\mathrm dt\approx0,72$

Das Sauerstoffdefizit ist somit durch ein Volumen von $0,72$ Litern gegeben.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?