Aufgabe 3: Quadratische Funktionen
Gegeben ist die Funktion 
mit 
a)
Berechne die Nullstellen der Funktion 
(3 P)
b)
- Gib die Koordinaten des Schnittpunktes des Graphen von
-Achse an.
- Zeichne den Graphen der Funktion
in das Koordinatensystem.
(3 P)
c)
Die Punkte 
und 
liegen auf dem Graphen der Funktion Die Punkte 
und 
sind Eckpunkte eines Dreiecks. Der Punkt 
ist der Mittelpunkt der Strecke 
Begründe, dass dieses Dreieck gleichschenklig und rechtwinklig ist.
Begründe, dass dieses Dreieck gleichschenklig und rechtwinklig ist.
(3 P)
d)
Weiterhin ist die quadratische Funktion 
mit 
mit 
gegeben. Die Funktion hat die Nullstellen 
und 
Ermittle die Werte für
und 
Ermittle die Werte für
(4 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Mit der 
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{4}{2}\pm\sqrt{\left(\dfrac{4}{2}\right)^2-3} \\[5pt]
&=& -2\pm 1 \\[5pt]
x_1&=& -1 \\[5pt]
x_2&=& -3
\end{array}\)](https://mathjax.schullv.de/553f50a3ee7abcdf777a5f5ca34fb0811d61dfe9142698e73d19b22c34b81a39?color=5a5a5a)
Die Funktion hat die Nullstellen 
und 
b)
Koordinaten des Schnittpunkts angeben
Schnittpunkt mit der -Achse: 
Graphen von 
zeichnen
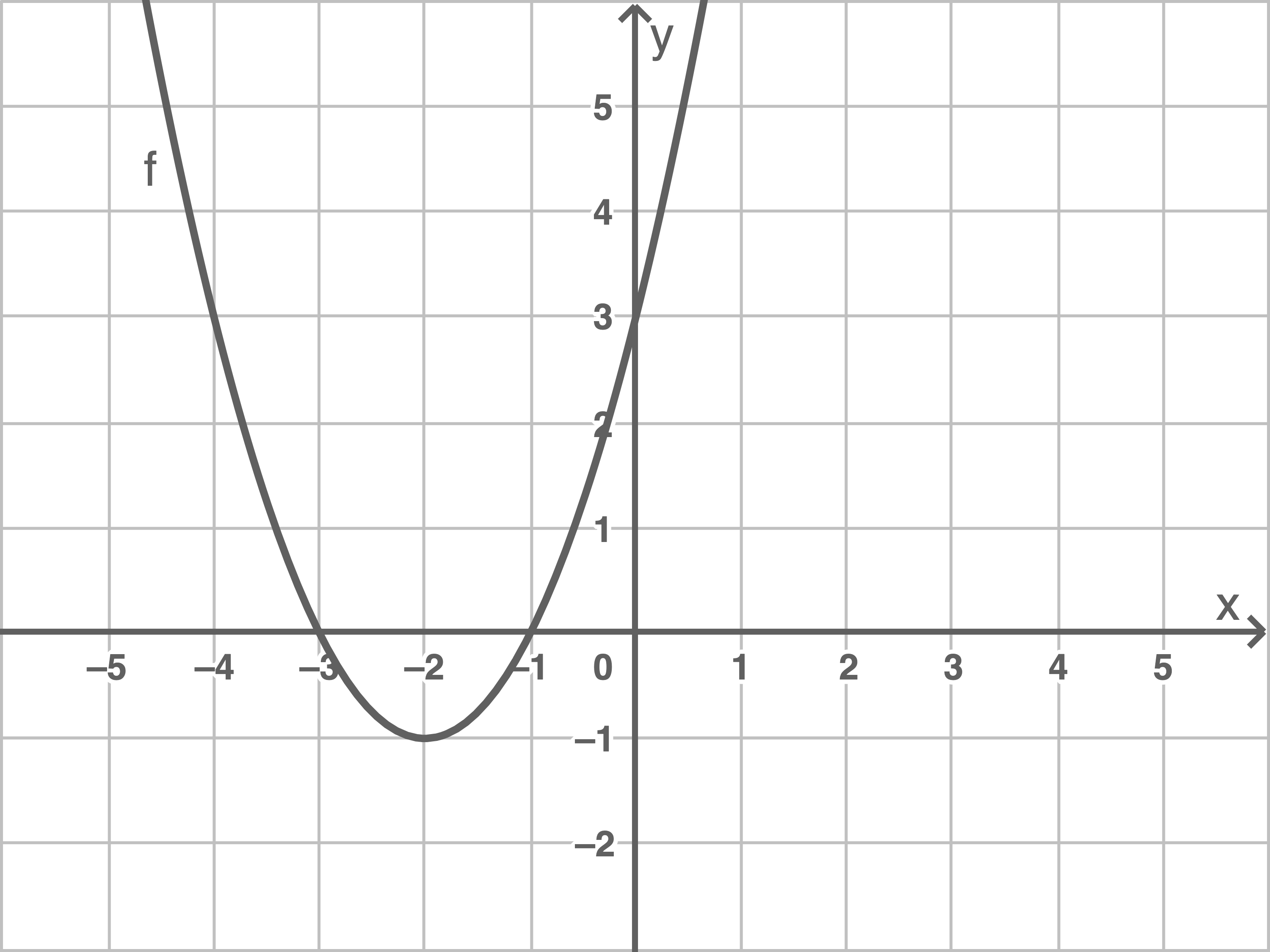
c)
Da genau zwischen 
und liegt, gilt 
Damit ist gezeigt, dass das Dreieck gleichschenklig ist.
Außerdem kann ein Halbkreis mit den Endpunkten und und dem Mittelpunkt gezeichnet werden, auf dem auch der Punkt liegt. Nach dem Satz des Thales ist das Dreieck daher auch rechtwinklig.
d)
Es müssen die folgenden Gleichungen gelten:
![\(\begin{array}[t]{rrl}
\text{I} & g(-2)&=& 0 \\[5pt]
&(-2)^2-2p+q&=& 0 \\[5pt]
& 4-2p+q&=& 0
\end{array}\)](https://mathjax.schullv.de/4aa532d4188e82a2bc46ddc9add7f850edb4a511544c3a04fb9c39e73b6cbf02?color=5a5a5a)
![\(\begin{array}[t]{rrl}
\text{II} & g(1)&=& 0 \\[5pt]
& 1^2+1\cdot p+q&=& 0 \\[5pt]
& 1+p+q&=& 0
\end{array}\)](https://mathjax.schullv.de/203e4566c94aff6861634b889a144840ee7fec2d939606b81fe2b82261789fa3?color=5a5a5a)
Gleichung 
nach 
umstellen:
![\(\begin{array}[t]{rll}
1+p+q&=& 0 \quad \scriptsize \mid\; -1-p \\[5pt]
q&=& -1-p
\end{array}\)](https://mathjax.schullv.de/dd3d08c70e34544813652c28b4cc7dae392cb1f864f89f393e2062a80dde409e?color=5a5a5a)
Einsetzen in 
liefert:
![\(\begin{array}[t]{rll}
4-2p-1-p&=& 0 \\[5pt]
3-3p&=& 0 \quad \scriptsize \mid\; +3p \\[5pt]
3&=& 3p \quad \scriptsize \mid\; :3 \\[5pt]
1&=& p
\end{array}\)](https://mathjax.schullv.de/34fa2cca1d0d270bfbeb3c45708a7c08b8b693ead7fb4165b8e7d123ae38361a?color=5a5a5a)
Einsetzen in liefert:
Die gesuchten Werte sind 
und 