Aufgabe 5: Messbecher
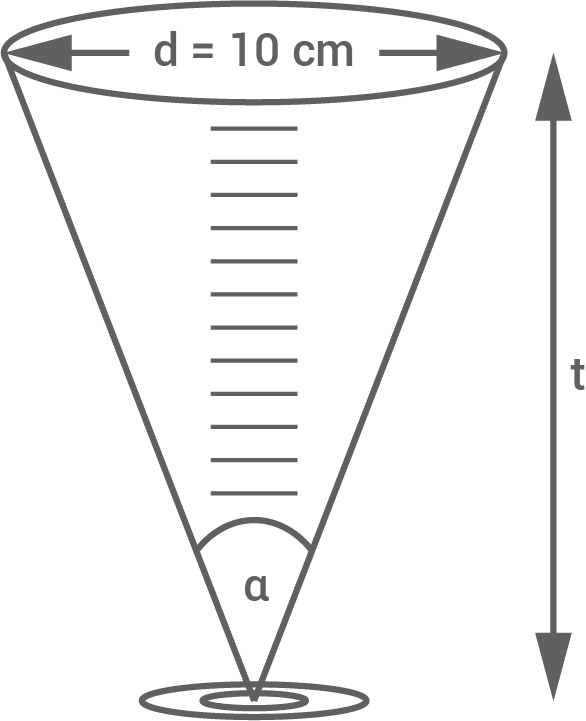
Zum Abmessen einer Flüssigkeit wird ein kegelförmiger Messbecher mit dem oberen Durchmesser 
und dem Winkel 
verwendet.
a)
Begründe, dass die Tiefe 
des Messbechers mit der Gleichung
berechnet werden kann.
Berechne das maximale Fassungsvermögen des Messbechers.
(5 P)
b)
Entlang einer Mantellinie des Messbechers sind Markierungen zum Fassungsvermögen angebracht.
Berechne die Länge der Mantellinie.
[Kontrollergebnis:
]
Bis zur Markierung 
wird eine Flüssigkeit eingefüllt. Die Füllhöhe beträgt dann 13,7 cm.
Berechne die Entfernung der-Markierung entlang der Mantellinie vom oberen Rand des Messbechers.
Berechne die Länge der Mantellinie.
[Kontrollergebnis:
Berechne die Entfernung der
(5 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Gleichung herleiten
des Messbechers berechnet werden:
Mit der Formel für das Volumen eines Kegels gilt:
![\(\begin{array}[t]{rll}
V&=&\dfrac{1}{3}\cdot\pi\cdot r^2\cdot t &\quad \scriptsize \\[5pt]
&\approx&\dfrac{1}{3}\cdot\pi\cdot (5\,\text{cm})^2\cdot 15,03\,\text{cm} &\quad \scriptsize \\[5pt]
&\approx& 393,5 \,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/f484ee426110f66ad7502a08a8eb3e5f126d03b0f4afc88c1ff3e53c3e72e4bd?color=5a5a5a)
Der Messbecher hat ein maximales Fassungsvermögen von 
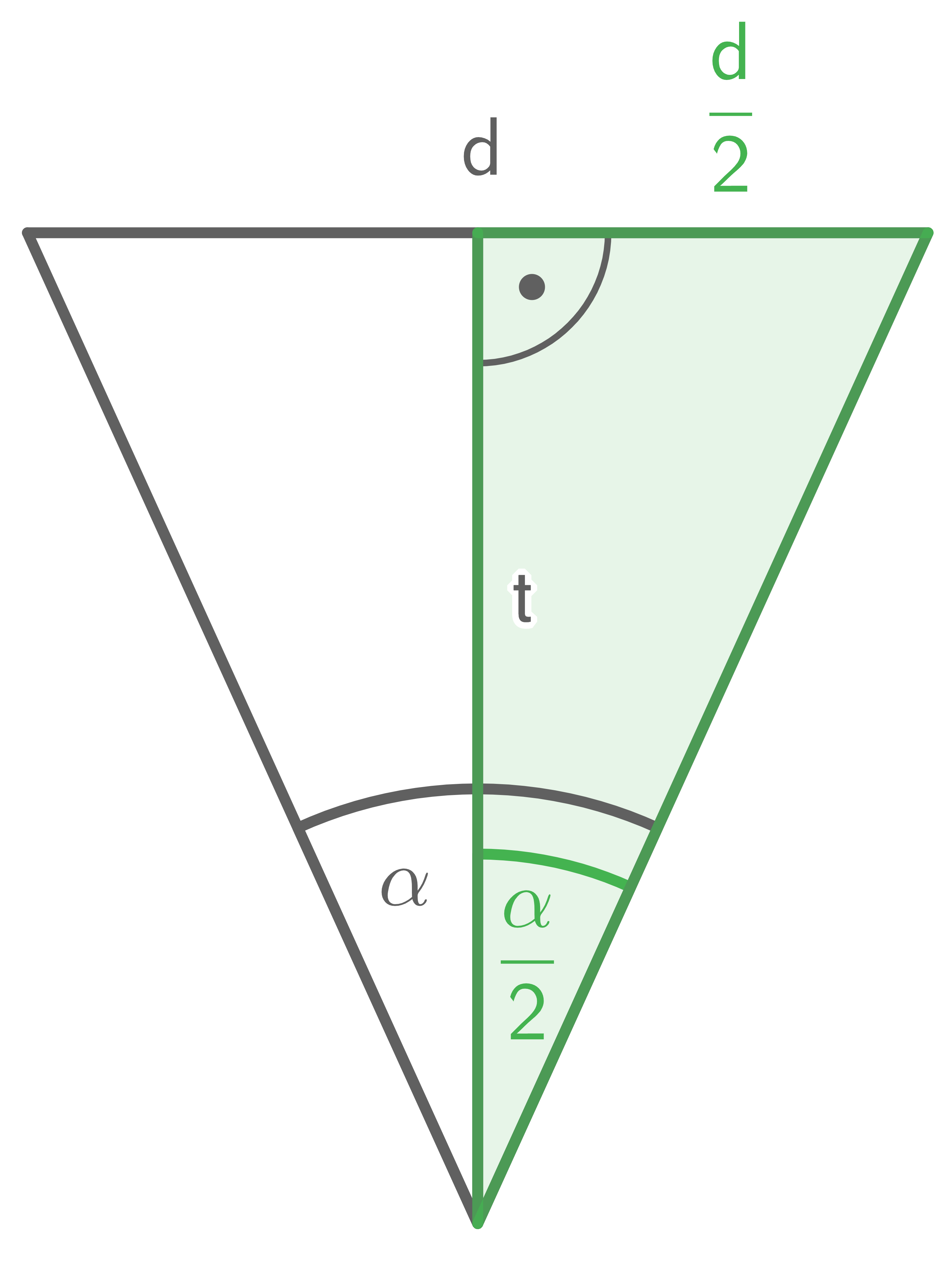
Projektion des Kegels in die Ebene
In dem gekennzeichneten Dreieck gilt:
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\alpha}{2}\right)&=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \\[5pt]
\tan\left(\dfrac{\alpha}{2}\right)&=& \dfrac{\frac{d}{2}}{t}
\end{array}\)](https://mathjax.schullv.de/33c271fcbf266a9e5c7b60ce96dcbf87a1cd72cf0e18bfd2e87822e27d581b32?color=5a5a5a)
Umstellen dieser Gleichung nach 
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\alpha}{2}\right)&=& \dfrac{\frac{d}{2}}{t} \quad \scriptsize \mid\;\cdot t \\[5pt]
\tan\left(\dfrac{\alpha}{2}\right)\cdot t&=& \dfrac{d}{2} \quad \scriptsize \mid\;:\tan\left(\dfrac{\alpha}{2}\right) \\[5pt]
t&=& \dfrac{\frac{d}{2}}{\tan\left(\dfrac{\alpha}{2}\right)} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/75b6fb443e2e4d0314bec21eef0a173b8e669604369025fd89cbd04f8d007820?color=5a5a5a)
Fassungsvermögen berechnen
Zunächst muss die Tiefe
b)
Länge der Mantellinie berechnen
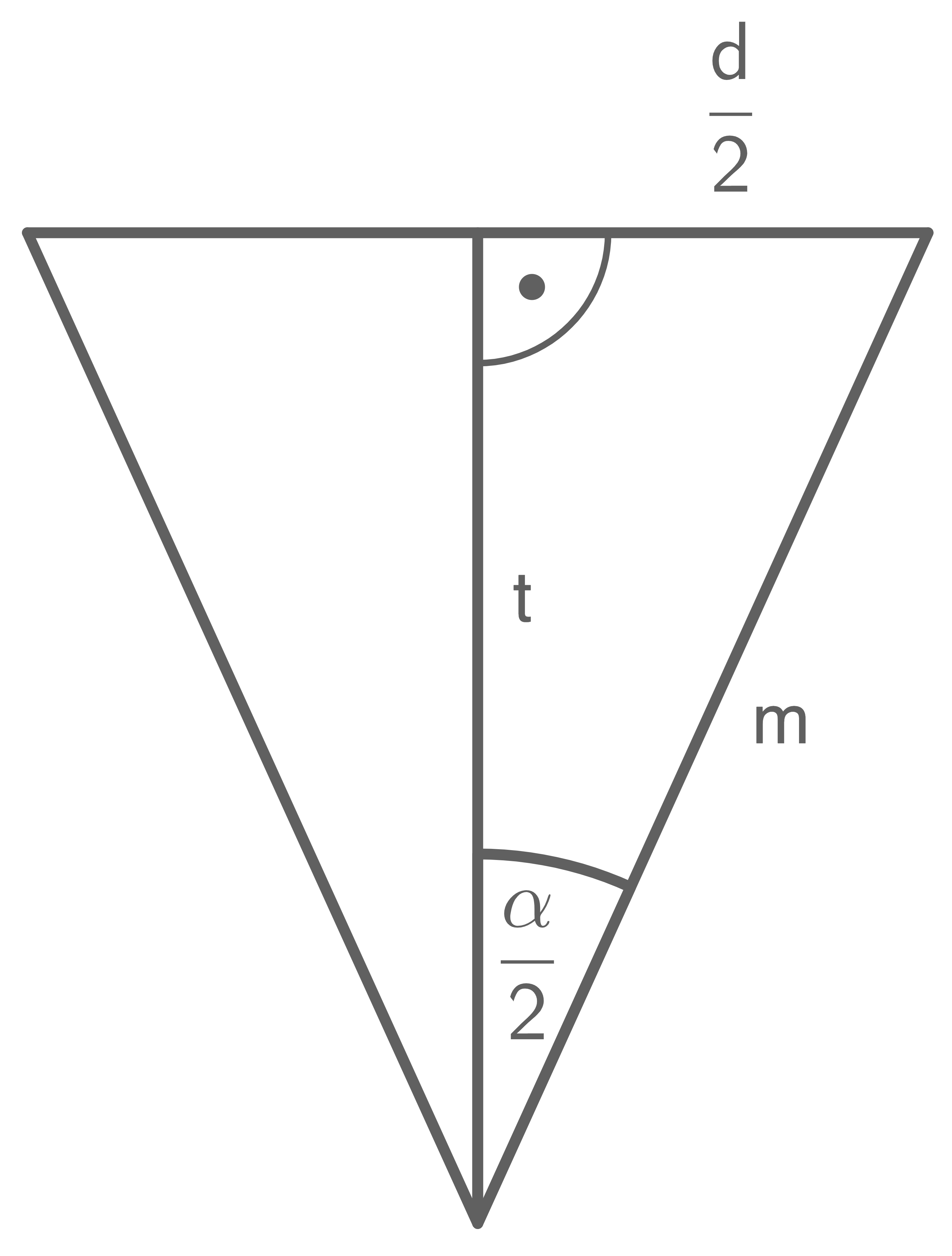
Der Abstand von der 
-Markierung zum oberen Rand beträgt 
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rll}
m^2&=& t^2+\left(\dfrac{d}{2}\right)^2 \\[5pt]
m^2&=& 15,03^2+\left(\dfrac{10}{2}\right)^2 \quad \scriptsize \mid\, \sqrt{\,} \\[5pt]
m&=&\sqrt{15,03^2+5^2} &\quad \scriptsize \\[5pt]
m&\approx& 15,84
\end{array}\)](https://mathjax.schullv.de/2bcba280c7fb513c6ffdd77368579e5cba722e732c47f0a62671d441870972ea?color=5a5a5a)
Die Mantellinie des Messbechers ist 
lang.
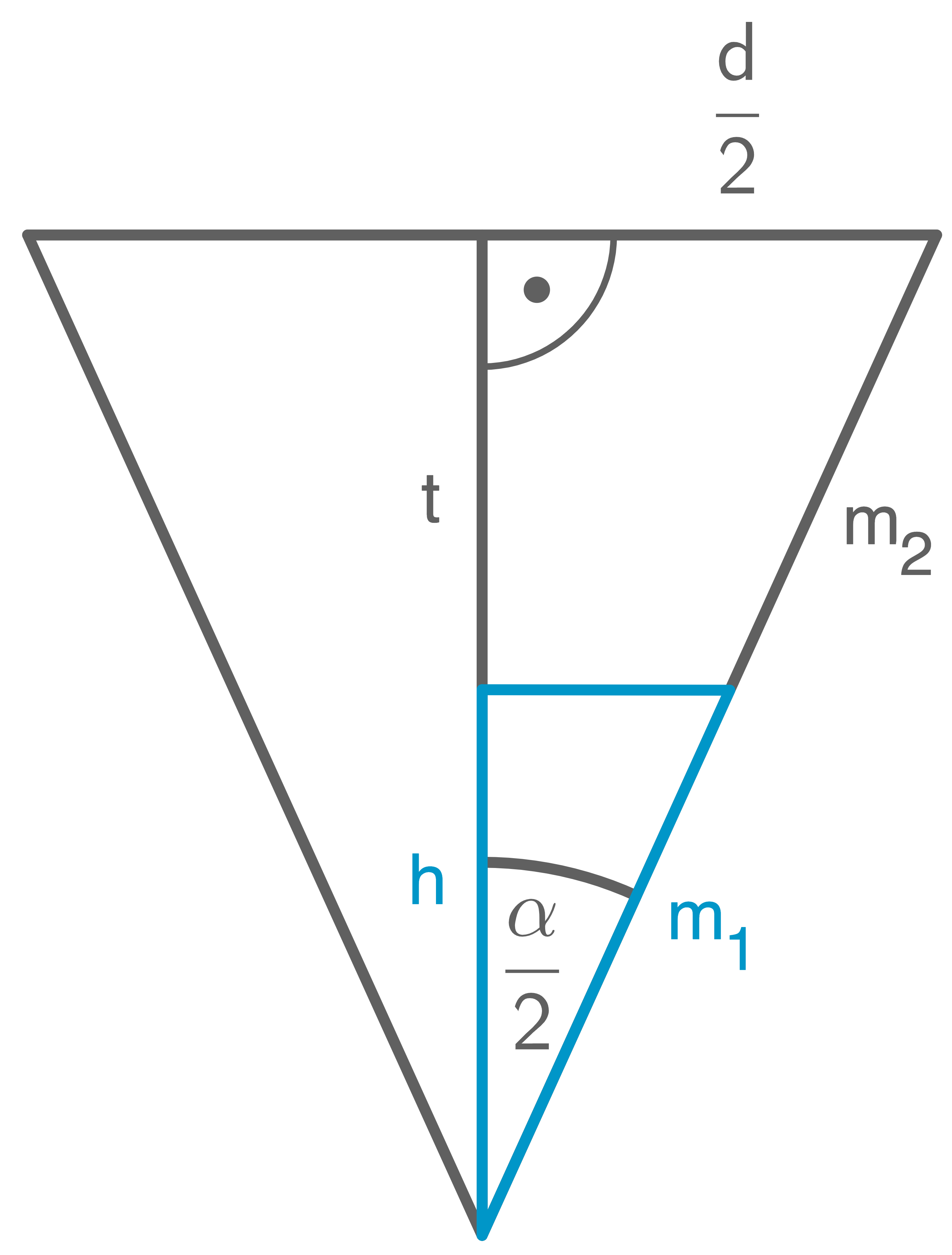
Berechnen der Entfernung der Markierung zum Rand
Gesucht ist die Länge der Strecke 
in der Abbildung. Dazu muss zunächst die Länge der Strecke 
berechnet werden. Es gilt:
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\alpha}{2}\right)&=& \dfrac{h}{m_1} \quad \scriptsize \mid\;\cdot m_1 \\[5pt]
\cos\left(\dfrac{\alpha}{2}\right)\cdot m_1&=& h \quad \scriptsize \mid\; :\cos\left(\dfrac{\alpha}{2}\right) \\[5pt]
m_1&=& \dfrac{h}{\cos\left(\dfrac{\alpha}{2}\right)} \\[5pt]
m_1&=& \dfrac{13,7\,\text{cm}}{\cos\left(\dfrac{36,8^°}{2}\right)} \\[5pt]
m_1 &\approx& 14,44\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/a69f8d45f972d60f50943b541185935fc30d2aaeb90a658a56ddcd4fc0680968?color=5a5a5a)
Damit folgt: