Aufgabe 6: Kugelstoßen
Emil und Franz trainieren an der Sportschule Kugelstoßen.
Während des Trainings wurde eine Flugbahn von Emils Kugel aufgezeichnet. Die Tabelle zeigt zu drei Zeitpunkten die horizontale Entfernung
der Kugel vom Abwurfpunkt und die zugehörige Höhe 
der Kugel über dem Boden.
Während des Trainings wurde eine Flugbahn von Emils Kugel aufgezeichnet. Die Tabelle zeigt zu drei Zeitpunkten die horizontale Entfernung
| Horizontale Entfernung x in m |
1 | 2 | 6 |
|---|---|---|---|
| Höhe h(x) in m | 3,5 | 4,7 | 1,5 |
a)
Die Flugbahn der Kugel kann durch eine Gleichung der Form 
beschrieben werden.
Zeige rechnerisch, dass der Punkt 
auf der Flugbahn der Kugel mit der Gleichung 
liegt.
Gib die Bedeutung des absoluten Gliedes 
im Sachzusammenhang an.
(3 P)
b)
Im Diagramm ist die Flugbahn der Kugel dargestellt.
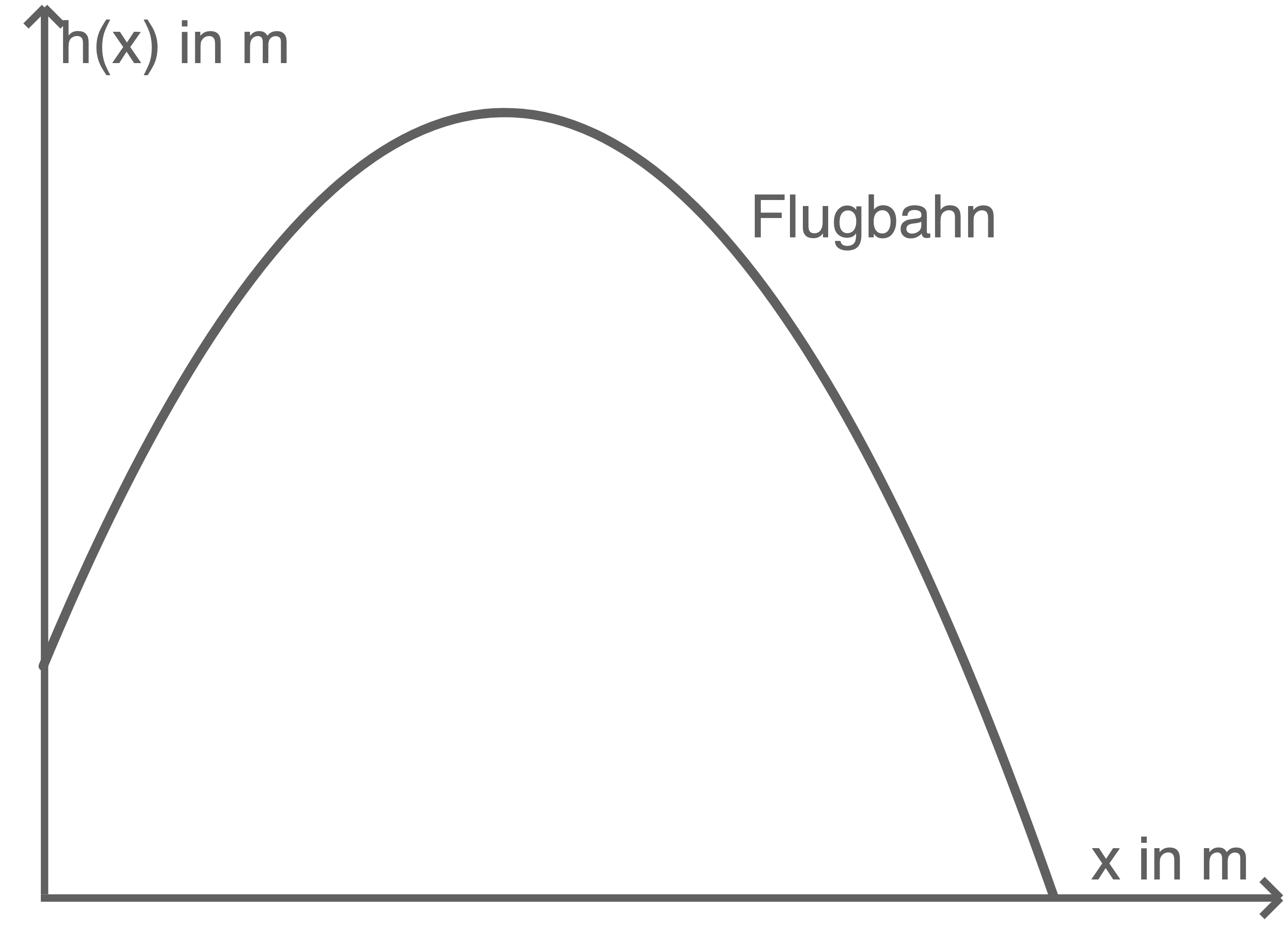
- Skaliere die Achsen des Koordinatensystems.
- Gib die maximale Höhe der Kugel bei diesem Wurf an.
(3 P)
c)
Franz hat die Stoßweite dieser Kugel folgendermaßen berechnet.
![\(\begin{array}[t]{rll}
0&=& -0,4x^2+2,4x+1,5&\quad \scriptsize \; \\[5pt]
0 &=&x^2-6x-3,75 &\quad \scriptsize\; \\[5pt]
x_{1/2} &=&3\pm\sqrt{9-3,75} &\quad \scriptsize \; \\[5pt]
x_1&=&5,29 &\quad \scriptsize \; \\[5pt]
x_2&=&0,71
\end{array}\)](https://mathjax.schullv.de/55c6c25bdab696f50dc0470a480bfb898567aaf19847f56f211f0c57e6b1f63c?color=5a5a5a)
Sein Ergebnis stimmt nicht mit der grafischen Darstellung der Flugbahn überein.
- Beschreibe den Fehler in der Rechnung.
- Berechne die Stoßweite dieser Kugel.
(3 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Zeigen, dass Punkt 
auf Graph von 
liegt
-Koordinate von Punkt 
in Gleichung von einsetzen:
![\(\begin{array}[t]{rll}
h(2)&=& -0,4\cdot2^2+2,4\cdot2+1,5 &\quad \scriptsize \\[5pt]
h(2)&=& 4,7
\end{array}\)](https://mathjax.schullv.de/c1d2840551c3fc7414967f4e19c229d1ea5bfee7b2a08faeb9b6caa9cbb1ea2f?color=5a5a5a)
Der Punkt liegt auf der Flugbahn der Kugel.
Bedeutung des absoluten Gliedes im Sachzusammenhang
beschreibt die Höhe, in der die Kugel abgeworfen wird.
b)
Achsen skalieren
Die Achsen lassen sich mit Hilfe des Scheitelpunkts skalieren. Dieser kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
h(x)&=& -0,4 x^2+2,4 x+1,5 \\[5pt]
&=& -0,4\cdot (x^2-6 x-3,75) \\[5pt]
&=& -0,4\cdot (x^2-6 x+9-9-3,75) \\[5pt]
&=& -0,4\cdot ((x-3)^2-9-3,75) \\[5pt]
&=& -0,4\cdot ((x-3)^2-12,75) \\[5pt]
&=& -0,4\cdot(x-3)^2+5,1
\end{array}\)](https://mathjax.schullv.de/4cd6da6980763a579fb20e7da85189139e8f231d6b3623c3cbb10e06b29167f1?color=5a5a5a)
Aus der Scheitelpunktform lassen sich direkt die Koordinaten 
des Scheitelpunkts ablesen.
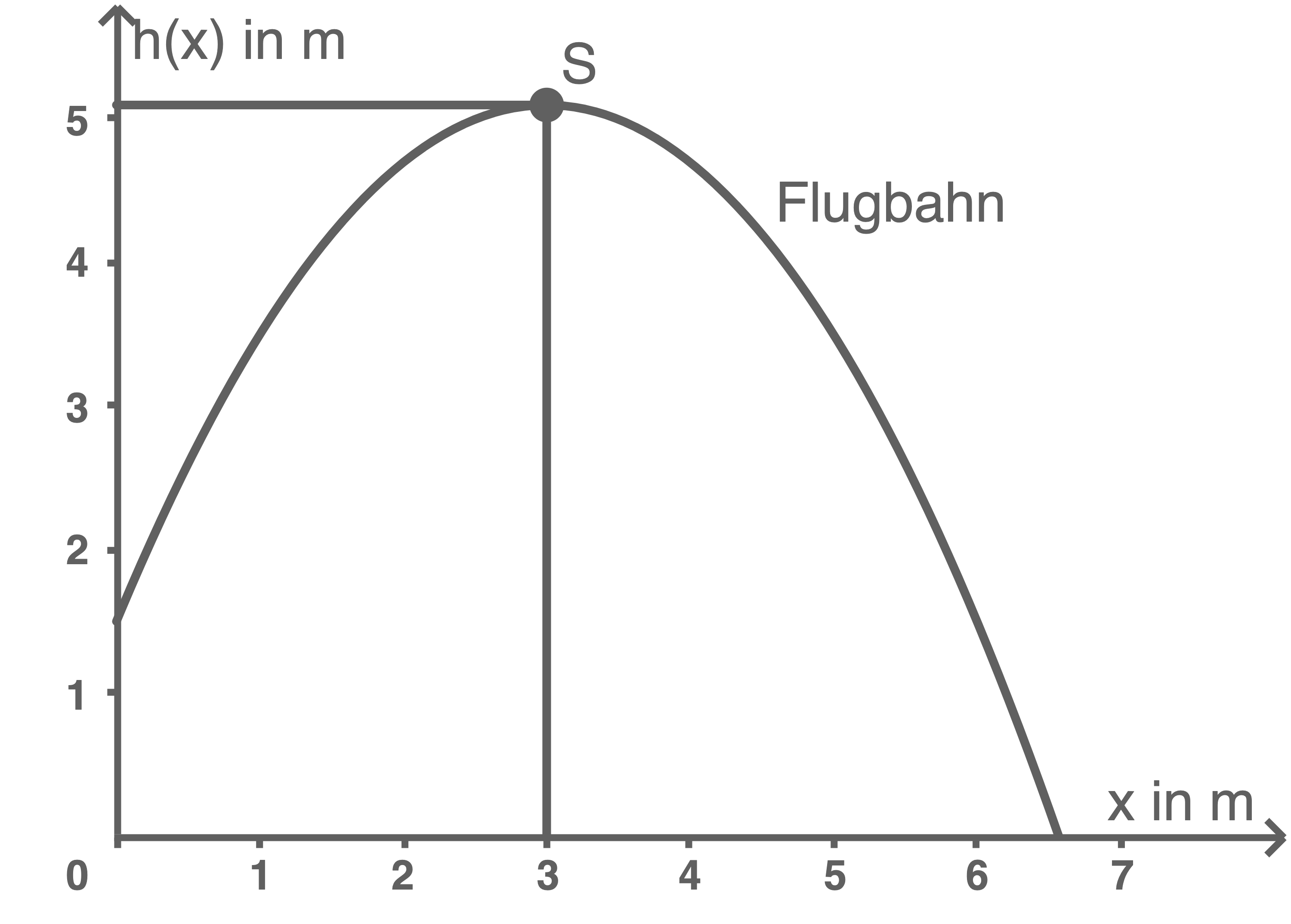Maximale Höhe der Kugel berechnen
Die maximale Höhe erreicht die Kugel im Scheitelpunkt. Sie beträgt 
c)
Der Fehler in der Rechnung ist das Minus in der 
-Formel. Da der Parameter 
selbst ein negatives Vorzeichen hat, muss sich unter der Wurzel eine Addition ergeben. Die richtige Rechnung lautet:
![\(\begin{array}[t]{rll}
0&=& -0,4x^2+2,4x+1,5&\quad \scriptsize \; \\[5pt]
0 &=&x^2-6x-3,75 &\quad \scriptsize\; \\[5pt]
x_{1/2} &=&-\dfrac{-6}{2}\pm\sqrt{\left(\dfrac{-6}{2}\right)^2-(-3,75)} &\quad \scriptsize \; \\[5pt]
x_{1/2} &=&3\pm\sqrt{9+3,75} &\quad \scriptsize \; \\[5pt]
x_1&=&6,57&\quad \scriptsize \; \\[5pt]
x_2&=&-0,57
\end{array}\)](https://mathjax.schullv.de/447537e0f4847de3c9931db396933d2d59fdc8b48471f9477614f36ab93698cc?color=5a5a5a)
Die Stoßweite der Kugel beträgt 