Aufgabe 5: Algerien
Algerien hat eine Fläche von 
Im Unterricht wurde die Fläche des Landes durch das unregelmäßige Sechseck
angenähert und in ein Dreieck, ein Trapez und ein unregelmäßiges Viereck zerlegt.
Folgende Längen und Winkel sind bekannt:
Im Unterricht wurde die Fläche des Landes durch das unregelmäßige Sechseck
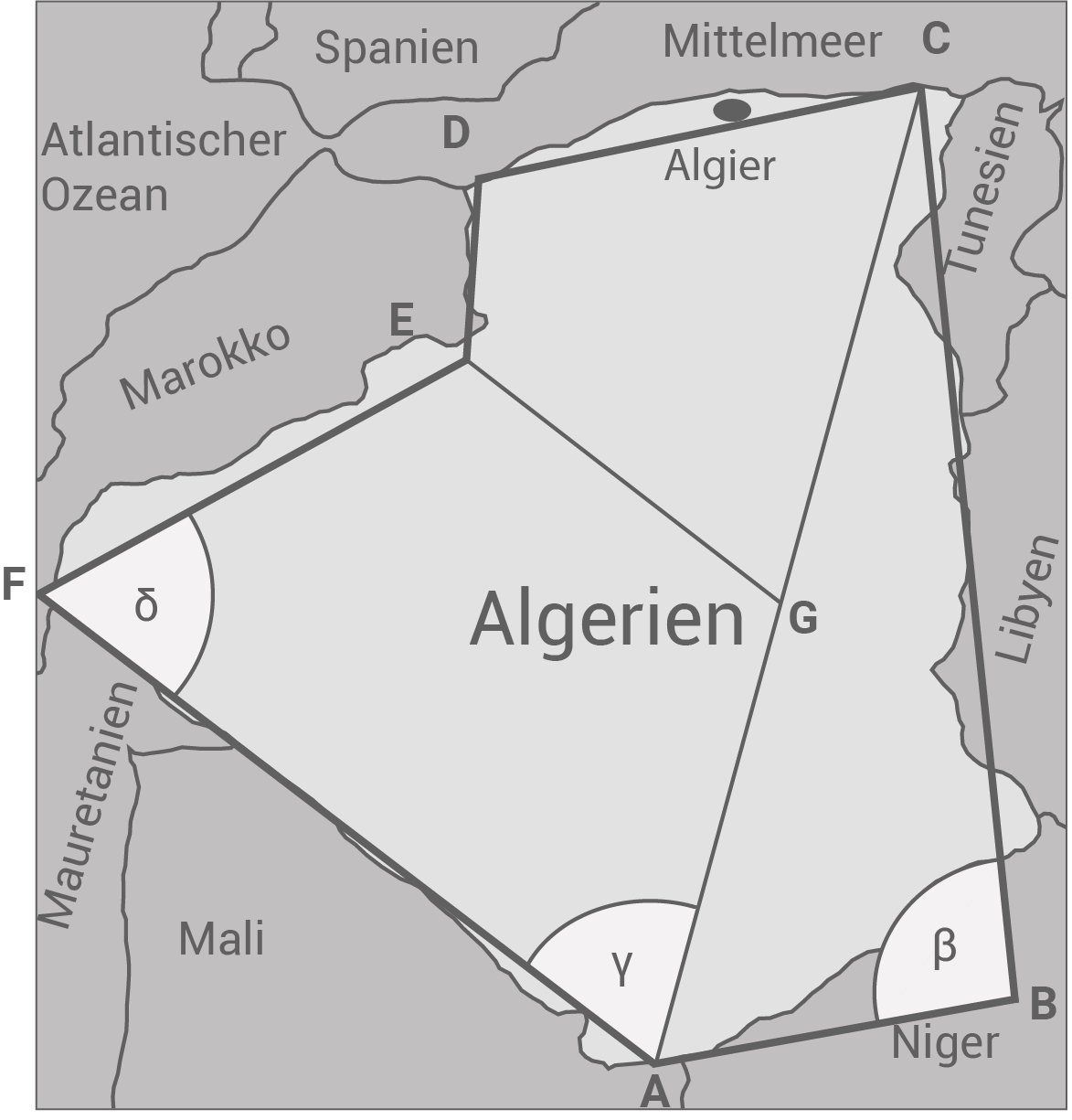
(Skizze nicht maßstabsgerecht)
a)
Der nördlichste Punkt des Landes kann modellhaft durch den Punkt 
und der südlichste durch den Punkt 
beschrieben werden.
Zeige, dass die Entfernung der Punkte und etwa 
beträgt.
Zeige, dass die Entfernung der Punkte
(2 P)
b)
Der Punkt 
ist der Mittelpunkt der Strecke 
und es gilt 
.
Ein Teil der Landesgrenze wird modellhaft durch die Strecke
beschrieben.
Begründe, dass dieser Teil eine Länge von
hat.
Ein Teil der Landesgrenze wird modellhaft durch die Strecke
Begründe, dass dieser Teil eine Länge von
(3 P)
c)
Die Größe der Fläche des Fünfecks 
wurde im Unterricht mit 
berechnet.
Zeige, dass der Flächeninhalt des Sechsecks weniger als 
von der tatsächlichen Fläche Algeriens abweicht.
(4 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Da das Dreieck 
rechtwinklig ist, gilt mit dem Satz des Pythagoras:
![\(\begin{array}[t]{rll}
\overline{AC}^2&=& \overline{AB}^2 + \overline{BC}^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\overline{AC}&=& \sqrt{\overline{AB}^2 + \overline{BC}^2} \\[5pt]
\overline{AC}&=& \sqrt{(695\,\text{km})^2 + (1980\,\text{km})^2} \\[5pt]
\overline{AC} &\approx& 2098,43\,\text{km} \approx 2100 \,\text{km} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eee6806b1b52e5be73ca9f049dcd94405bdeca20b1147e2dc996ee0e6d894405?color=5a5a5a)
b)
Wegen 
handelt es sich bei der Fläche 
um ein Trapez, das wegen 
gleichschenklig ist. Es gilt also 
![\(\begin{array}[t]{rll}
\overline{EF}&=& \overline{AG} &\quad \scriptsize \\[5pt]
&=&\dfrac{\overline{AC}}{2} &\quad \scriptsize \\[5pt]
&=&\dfrac{2100\,\text{km}}{2} &\quad \scriptsize \\[5pt]
&=& 1050\,\text{km}
\end{array}\)](https://mathjax.schullv.de/59bd6da7dc8137d54ecd4f2ecafe0b4f10db5c0a36dd46229eb83ffbd5e29b46?color=5a5a5a)
c)
1. Schritt: Flächeninhalt des Dreiecks 
berechnen
![\(\begin{array}[t]{rll}
A_{ABC}&=& \dfrac{1}{2}\cdot \overline{AB}\cdot \overline{BC} &\quad \scriptsize \\[5pt]
A_{ABC}&=& \dfrac{1}{2}\cdot 695\,\text{km}\cdot 1980 \,\text{km} &\quad \scriptsize \\[5pt]
A_{ABC}&=& 688\;050 \,\text{km}^2
\end{array}\)](https://mathjax.schullv.de/48ffcec28a4ccae7025f21965e9cbd913eb3fb46cd858f7f98e7d9a81940ef89?color=5a5a5a)
2. Schritt: Flächeninhalt des Sechsecks 
berechnen
![\(\begin{array}[t]{rll}
A&=& A_{ABC}+ A_{ACDEF} &\quad \scriptsize \\[5pt]
A&=& 688\;050 \,\text{km}^2 + 1\;739\;232\,\text{km}^2 &\quad \scriptsize \\[5pt]
A&=& 2\;427\;282\,\text{km}^2
\end{array}\)](https://mathjax.schullv.de/bd5b9e7dc8891d54cf1ed890818ea8e2e90d3f05a2ed2e10b1aa274326122cb7?color=5a5a5a)
3. Schritt: Aussage nachweisen
Da 
ist, ist die Aussage nachgewiesen.