Aufgabe 3: Quadratische Funktionen
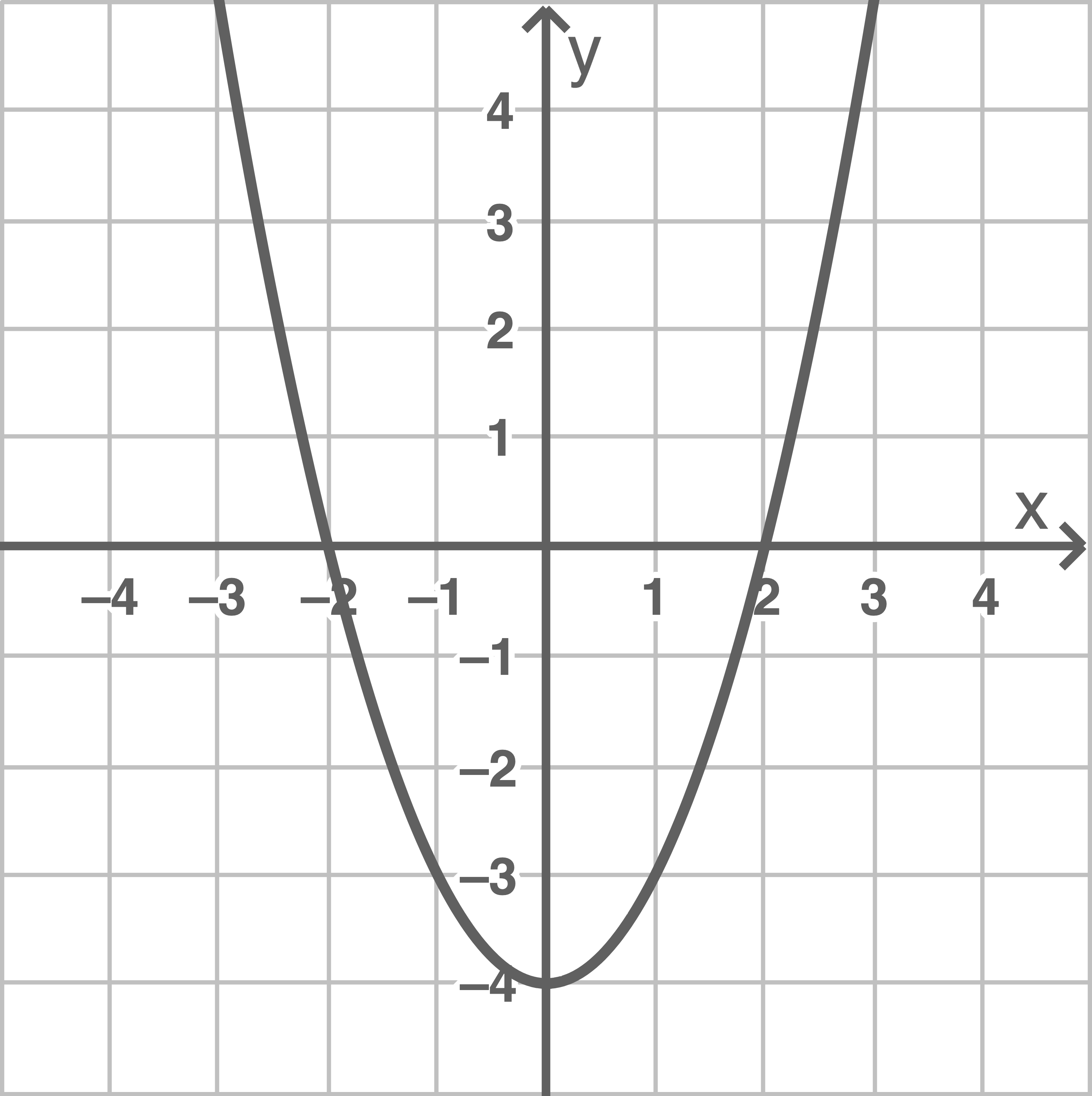
Gegeben ist die Funktion  mit
mit  . Der Graph der Funktion
. Der Graph der Funktion  ist im Koordinatensystem dargestellt.
ist im Koordinatensystem dargestellt.

a)
Weise rechnerisch nach, dass der Punkt  auf dem Graphen von
auf dem Graphen von  liegt.
Der Punkt
liegt.
Der Punkt  liegt ebenfalls auf dem Graphen von
liegt ebenfalls auf dem Graphen von  . Gib die fehlende Koordinate
. Gib die fehlende Koordinate  an. Begründe deine Angabe ohne Rechnung.
an. Begründe deine Angabe ohne Rechnung.
(3 P)
b)
Zeige rechnerisch, dass  und
und  Nullstellen der Funktion
Nullstellen der Funktion  sind.
sind.
(2 P)
c)
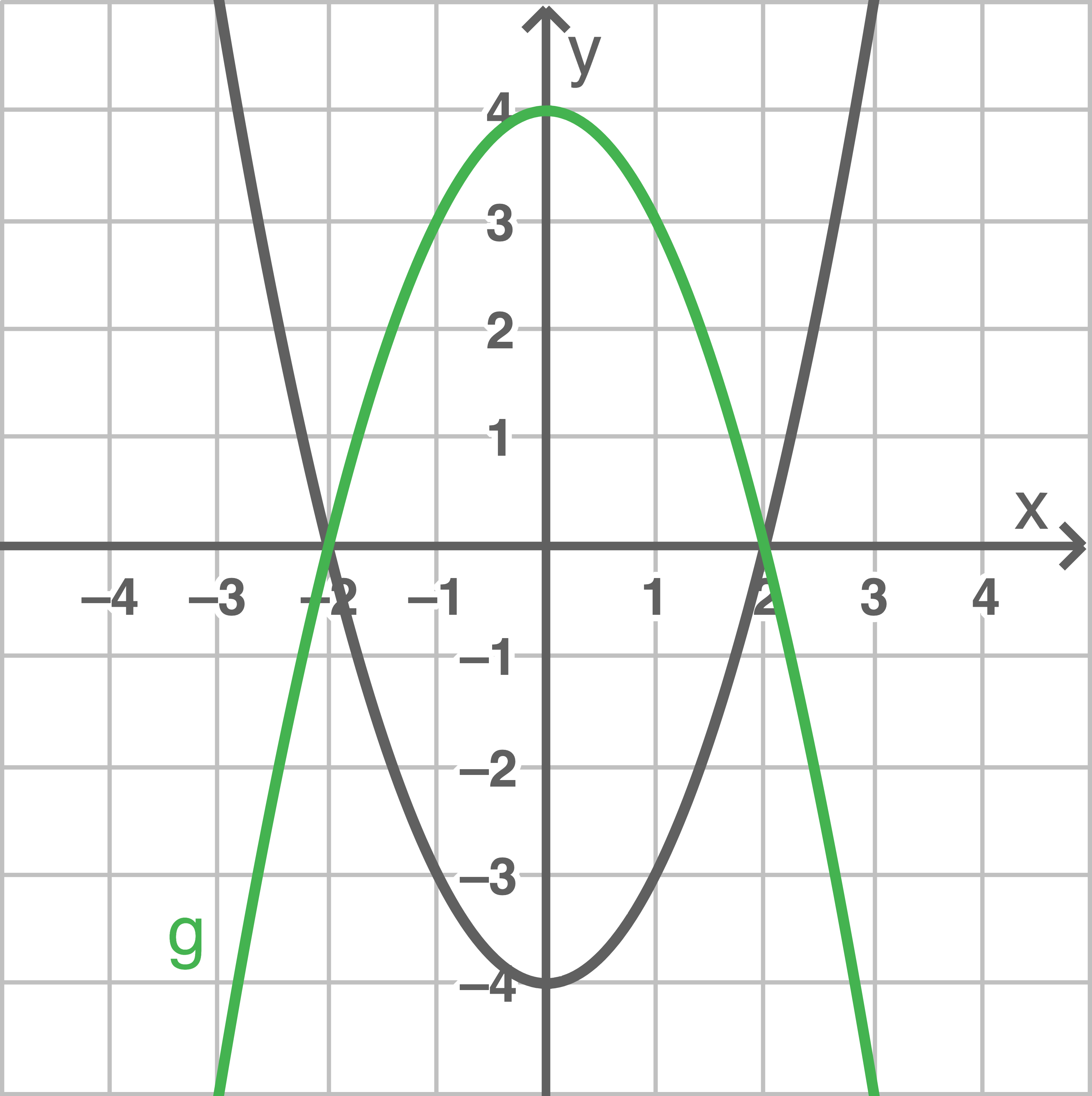
Der Graph der Funktion  entsteht durch Spiegelung des Graphen der Funktion
entsteht durch Spiegelung des Graphen der Funktion  an der
an der  -Achse.
-Achse.
- Zeichne den Graphen der Funktion
in das gegebene Koordinatensystem ein.
Gib eine Gleichung der Funktionan.
- Die Schnittpunkte der Graphen der Funktionen
und
mit den beiden Koordinatenachsen sind Eckpunkte eines Vierecks.
Zeichne dieses Viereck in das gegebene Koordinatensystem ein. Berechne den Flächeninhalt dieses Vierecks.
(6 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Nachweisen, dass der Punkt auf dem Graphen liegt
Punktprobe durchführen:
 Fehlende Koordinate angeben und begründen
Die fehlende Koordinate ist durch
Fehlende Koordinate angeben und begründen
Die fehlende Koordinate ist durch  gegeben, da der Graph von
gegeben, da der Graph von  symmetrisch zur
symmetrisch zur  -Achse ist.
-Achse ist.
b)
c)
Graphen von  einzeichnen und Funktionsgleichung angeben
einzeichnen und Funktionsgleichung angeben
 Viereck einzeichnen und Flächeninhalt berechnen
Viereck einzeichnen und Flächeninhalt berechnen
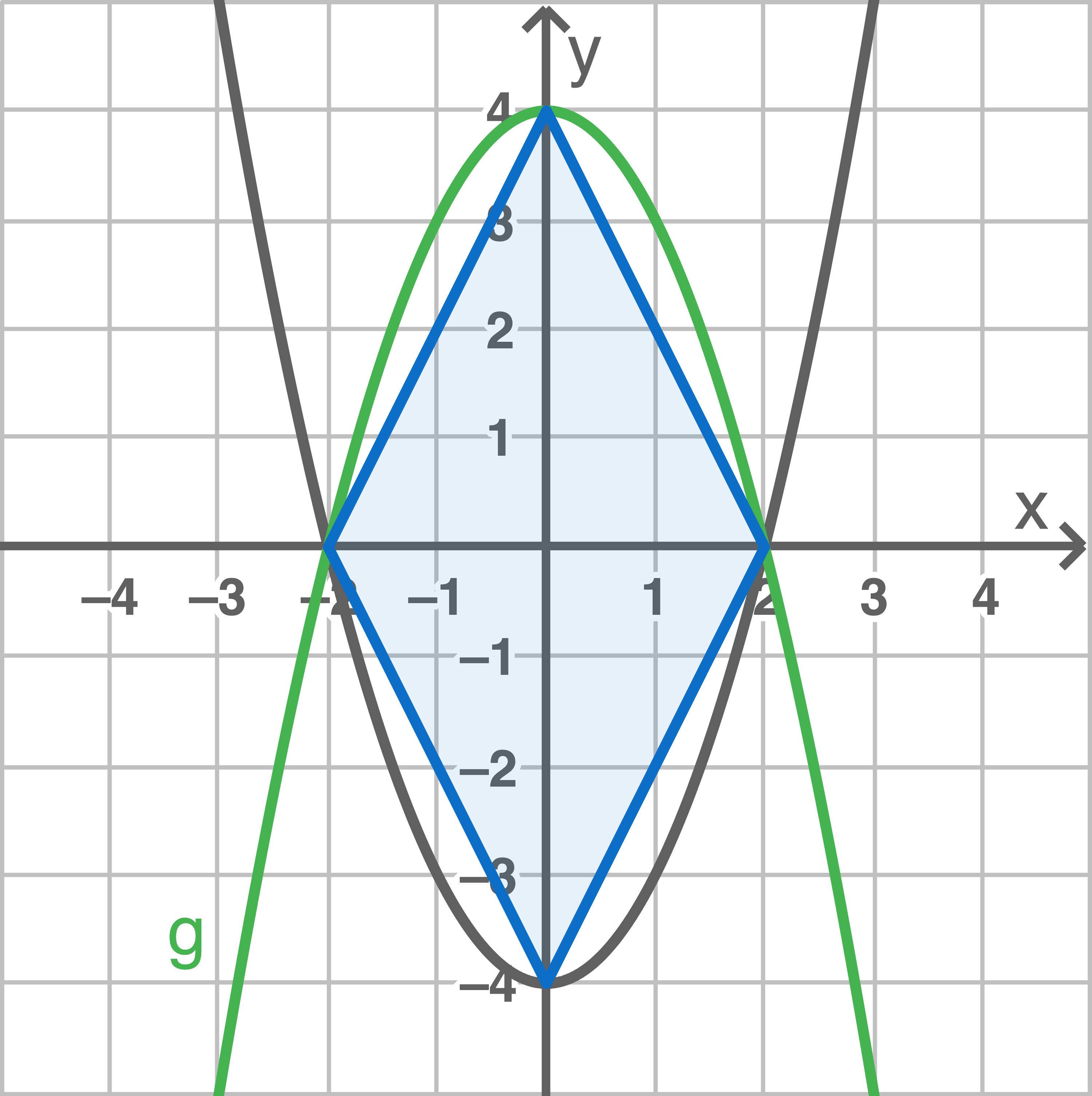 Das Viereck kann in vier rechtwinklige Dreiecke unterteilt werden. Der Flächeninhalt des Vierecks lässt sich damit wie folgt berechnen:
Das Viereck kann in vier rechtwinklige Dreiecke unterteilt werden. Der Flächeninhalt des Vierecks lässt sich damit wie folgt berechnen:
![\(A = 4\cdot \left(\dfrac{1}{2}\cdot 2\cdot 4\right) =16\,\text{[FE]}\)](https://www.schullv.de/resources/formulas/319d76e9cddc638e8506c0e982b4792f6e96a97b31d6cb99d5821d81296fa4d7_light.svg)

