A – Pflichtaufgaben

Analysis (Niveau 1)

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ durch $f_a(x)=x \cdot \mathrm e^{-a \cdot x^2}$ mit $a \in \mathbb{R}$ und $\mathrm{a}\gt0.$ Jeder Graph der Schar verläuft durch den Koordinatenursprung.

1.1

Zeige, dass alle Graphen der Schar im Koordinatenursprung die gleiche Steigung haben.

(2 BE)

1.2

Zeige, dass alle Graphen der Schar punktsymmetrisch zum Koordinatenursprung sind.

(3 BE)

Analysis (Niveau 1)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{1}{4} x^3-3 x.$

2.1

Es gilt $\(f$ Zeige, dass $2$ eine Extremstelle von $f$ ist.

(2 BE)

2.2

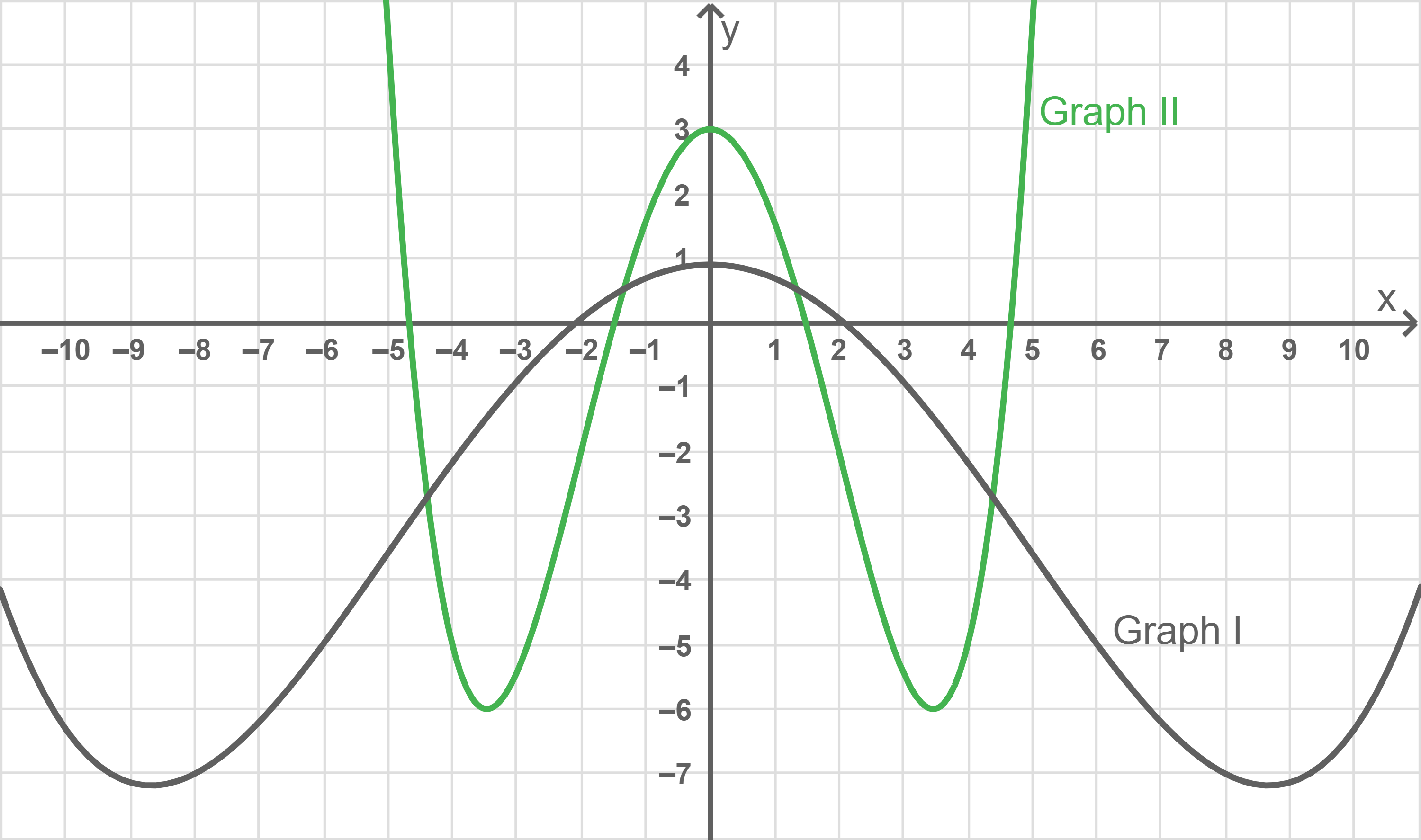
Einer der Graphen I und II in der Abbildung ist der Graph einer Stammfunktion von $f.$ Gib diesen Graphen an und begründe deine Angabe.

(3 BE)

Lineare Algebra/Analytische Geometrie (Niveau 1)

Gegeben sind der Vektor $\overrightarrow{v}=\pmatrix{6\\a}$ mit $a\gt0$ und die Matrix $M=\pmatrix{0 & b\\2 & 0}$ mit $b \in \mathbb{R}.$

3.1

Bestimme den Wert von $a,$ sodass $\vert\overrightarrow{v}\vert=10.$

(2 BE)

3.2

Ermittle für $a=5$ den Wert von $b,$ sodass die Vektoren $\overrightarrow{v}$ und $M\cdot \overrightarrow{v}$ zueinander orthogonal sind.

(3 BE)

Stochastik (Niveau 1)

Bei einem Spiel wird ein (fairer) Würfel zweimal geworfen. Die Seiten des Würfels sind mit den Zahlen von 1 bis 6 durchnummeriert.

4.1

Begründe, dass die Wahrscheinlichkeit dafür, bei keinem der beiden Würfe die Zahl 3 zu erzielen, $\frac{25}{36}$ beträgt.

(2 BE)

4.2

Der Einsatz bei diesem Spiel beträgt 2 Euro. Je nachdem, wie oft dabei die Zahl 3 erzielt wird, werden folgende Auszahlungen getätigt:

Anzahl der Würfe, bei denen die Zahl 3 erzielt wird	Auszahlung in Euro
$0$	$0$
$1$	$5$
$2$	$x$

Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen. Ermittle den Wert von $x.$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Analysis (Niveau 1)

1.1

Für die Ableitung von $f_a$ folgt mit der Produktregel:

$\(\begin{array}[t]{rlll} f_a$

Einsetzen von $x=0$ liefert:

$\(\begin{array}[t]{rlll} f_a$

Somit haben alle Graphen der Schar im Ursprung die gleiche Steigung.

1.2

$\begin{array}[t]{rlll} f_a(-x)&=&(-x)\cdot\mathrm e^{-a\cdot(-x)^2} \\[5pt] &=&-x\cdot\mathrm e^{-a\cdot x^2} \\[5pt] &=&-f_a(x) \end{array}$

Analysis (Niveau 1)

2.1

Für die erste Ableitung von $f$ gilt:

$\(\begin{array}[t]{rlll} f$

Einsetzen von $x=2$ liefert:

$\(\begin{array}[t]{rlll} f$

Somit ist die notwendige Bendingung für Extremstellen in $x=2$ erfüllt. Da die hinreichende Bedingung für Extremstellen bereits in der Aufgabenstellung gegeben ist, folgt somit, dass $2$ eine Extremstelle von $f$ ist.

2.2

Da $f$ bei $x=2$ eine Extremstelle besitzt, hat jede Stammfunktion von $f$ bei $x=2$ eine Wendestelle. Aus der Abbildung folgt somit, dass Graph II der Graph einer Stammfunktion von $f$ ist.

Lineare Algebra/Analytische Geometrie (Niveau 1)

3.1

$\begin{array}[t]{rlll} \left\vert\overrightarrow{v}\right\vert&=&10 \\[5pt] \sqrt{6^2+a^2}&=&10 &\mid\;^2 \\[5pt] 36+a^2&=&100 &\mid\;-36 \\[5pt] a^2&=&64 &\mid\;\sqrt{\;}\\[5pt] a&=&\pm8 \end{array}$

Da $a\gt0$ gelten soll, folgt somit $a=8.$

3.2

$\begin{array}[t]{rlll} M\cdot\overrightarrow{v}&=&\pmatrix{0 & b\\2 & 0}\cdot\pmatrix{6\\5} \\[5pt] &=&\pmatrix{5b\\6\cdot2} \\[5pt] &=&\pmatrix{5b\\12} \end{array}$

Damit folgt für den gesuchten Wert von $b:$

$\begin{array}[t]{rlll} \overrightarrow{v}\circ M\cdot\overrightarrow{v}&=&0 \\[5pt] \pmatrix{6\\5}\circ\pmatrix{5b\\12}&=&0 \\[5pt] 30b+60&=&0 &\mid\;-60 \\[5pt] 30b&=&-60 &\mid\;:30 \\[5pt] b&=&-2 \end{array}$

Stochastik (Niveau 1)

4.1

Die Wahrscheinlichkeit, bei einem einzelnen Wurf keine 3 zu würfeln, beträgt $\frac{5}{6}.$ Damit beträgt die Wahrscheinlichkeit in beiden Würfen keine 3 zu erzielen $\frac{5}{6}\cdot\frac{5}{6}=\frac{25}{36}.$

4.2

Die Wahrscheinlichkeit, in beiden Würfen eine 3 zu erzielen, beträgt $\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{36}.$ Zusammen mit der Wahrscheinlichkeit aus Teilaufgabe 4.1 ergibt sich somit $1-\frac{26}{36}=\frac{10}{36}$ als Wahrscheinlichkeit für genau eine 3 in zwei Würfen.
Die erwartete Auszahlung pro Spiel soll gleich dem Einsatz, d.h. $2\,\text{€},$ sein. Somit folgt für $x:$

Rechenweg anzeigen

$x=22$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?