B2 - Analysis

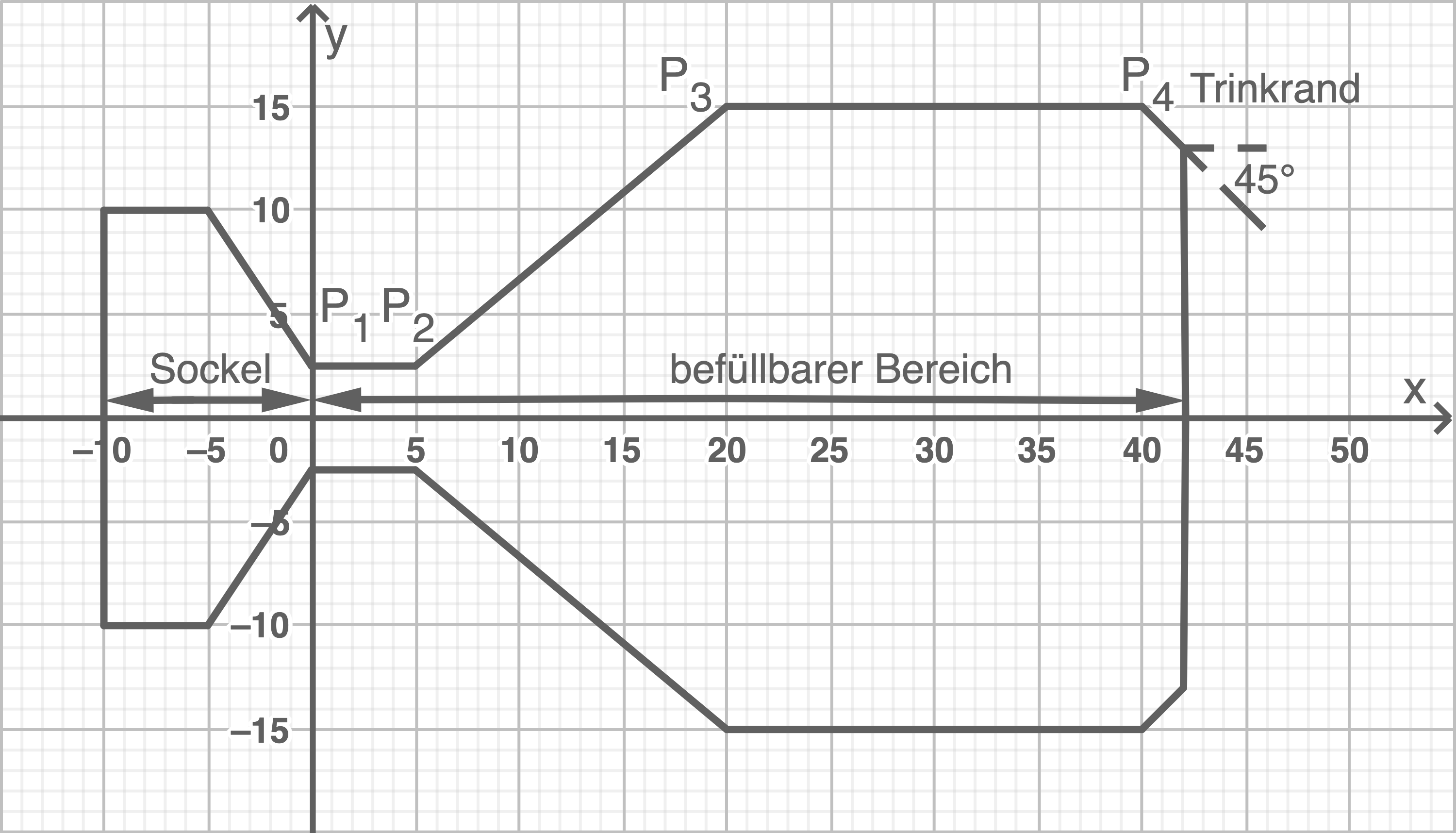
Für den Pokal einer Sportveranstaltung soll ein Rotationskörper entworfen werden, der aus einem $10\,\text{cm}$ hohen Sockel und einem befüllbaren Bereich zusammengesetzt ist. Der Pokal soll insgesamt $52\,\text{cm}$ hoch sein. Material 1 zeigt den Querschnitt eines schematischen Entwurfs eines um $90^\circ$ nach rechts gekippten Pokals. Der Querschnitt enthält die Symmetrieachse des Pokals. Im Querschnitt sind die markanten Eckpunkte der Profillinie des Sportpokals $P_1(0\mid 2,5),$ $P_2(5\mid 2,5),$ $P_3(20\mid 15)$ und $P_4(20\mid 15)$ durch die in Material 1 eingezeichneten Strecken verbunden. Bei den folgenden Modellierungen wird versucht, die eckige Profillinie des befüllbaren Bereichs abzurunden. Alle Maße sind in $\text{cm}$ angegeben.

Berechne den Inhalt der Querschnittsfläche des befüllbaren Bereichs. (Material 1)
[zur Kontrolle: $A = 943,5\,\text{cm}^2$ ]

(5 BE)

2.1

Ermittle die Funktionsgleichung einer ganzrationalen Funktion vierten Grades $f$ , deren Graph die Profillinie des befüllbaren Bereichs oberhalb der $x$ -Achse unter Einhaltung folgender Vorgaben modelliert:

Die Profillinie verläuft durch die Punkte $P_1(0\mid 2,5)$ , $P_2(5\mid 2,5)$ , $P_3(20\mid 15)$ und $P_4(40\mid 15)$ , der Winkel am Trinkrand soll $45^\circ$ betragen (Material 1).

Die Parameter in der Funktionsgleichung sollen auf $6$ Nachkommastellen gerundet werden. Begründe, dass der Grad der ganzrationalen Funktion nicht kleiner als vier sein kann.

(10 BE)

2.2

Bestimme das bei Verwendung der Funktion $f$ entstehende Gesamtvolumen des befüllbaren Bereichs des Pokals. Die Dicke der Wandstärke des Pokals soll nicht berücksichtigt werden.

[Falls du die Funktionsgleichung in Aufgabe 2.1 nicht bestimmen konntest, verwende die Ersatzfunktion $f_E$ mit

$f_E(x)=...$ .]

Gleichung anzeigen

(3 BE)

Der Graph der Funktion $f$ aus Aufgabe 2.1 legt die Vermutung nahe, dass man die Profillinie des befüllbaren Bereichs auch durch eine geeignete trigonometrische Funktion $s$ mit $s(x)=A\cdot \sin(k\cdot x-b)+c$ modellieren kann.

3.1

Erläutere folgende Überlegungen zur Bestimmung des Parameters $c:$

(1)

Zunächst werden die Nullstellen von $\(f$ im Intervall $[0;42]$ bestimmt.

(2)

Dann werden die Funktionswerte an diesen beiden Nullstellen bestimmt.

(3)

Der Parameter $c$ wird als Mittelwert der in (2) bestimmten Funktionswerte bestimmt.

Erläutere, wie man auf der Grundlage dieser Überlegungen anhand des Graphen von $f$ den Parameter $k$ der Funktion $s$ bestimmen kann.

(8 BE)

3.2

Für einen möglichen Entwurf des Pokals sind folgende Werte für die Parameter der Funktion $s$ gegeben: $A=8,79$ ; $b=8,165$ ; $c=10,739$ Die Periodenlänge beträgt $55,7613$ .

Bestimme unter Angabe einer Stammfunktion mit diesen Werten den Inhalt der Querschnittsfläche des befüllbaren Bereichs des Pokals für die Modellierung mit der Funktion $s$ .

(4 BE)

3.3

Untersuche bei welcher der beiden Modellierungen der Profillinie (Aufgabe 2.1 und Aufgabe 3.2) die größere relative Abweichung des Inhalts der Querschnittsfläche von dem in Aufgabe 1 ermittelten Wert auftritt.
[Falls du die Funktionsgleichung in Aufgabe 2.1 nicht bestimmen konntest, verwende die Ersatzfunktion $f_E$ mit

$f_E(x)=...$ .]

Gleichung anzeigen

(7 BE)

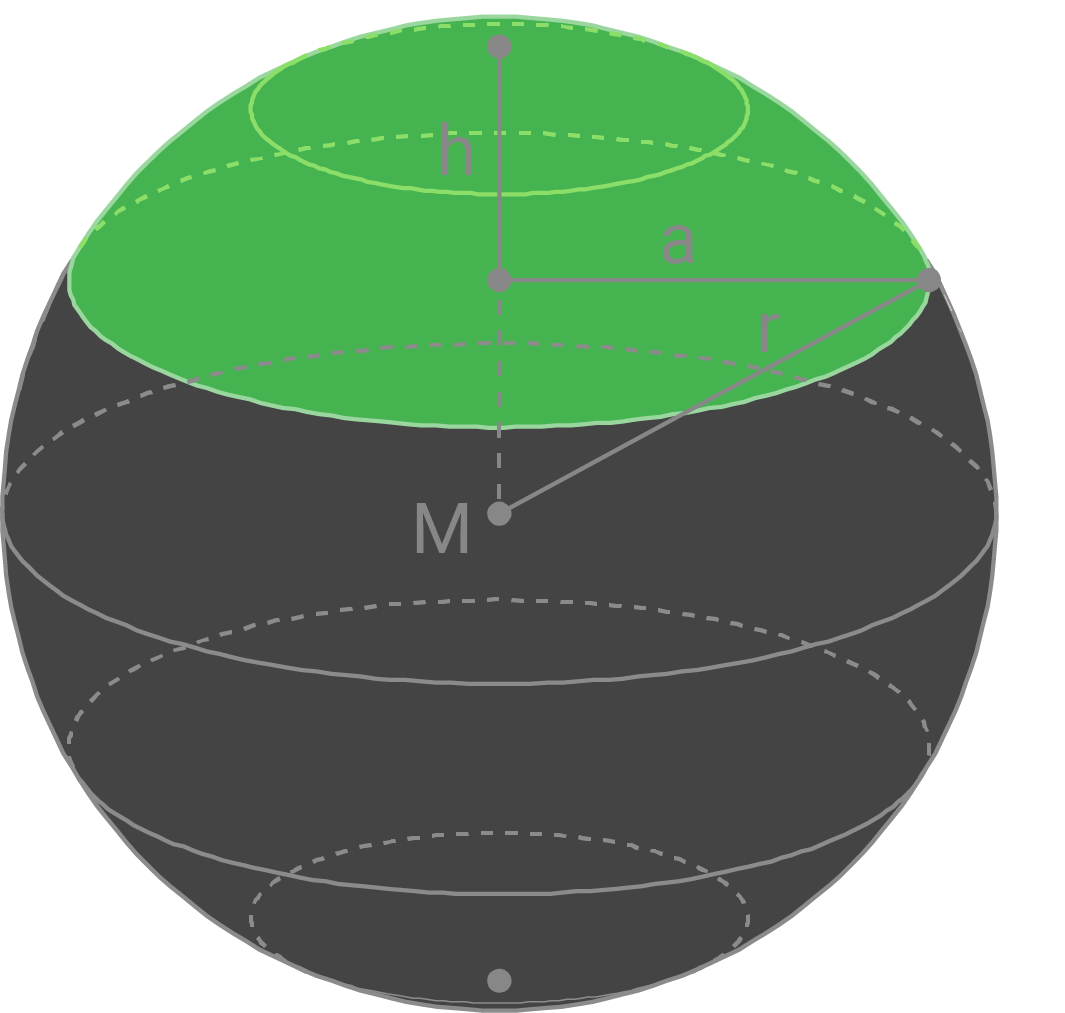
Für einen Sportpokal, dessen Profillinie mithilfe der Sinusfunktion $s$ aus Aufgabe 3.2 modelliert wird, soll ein Deckel in Form einer Kugelkappe angefertigt werden. (Material 2)

4.1

Bestimme den Wert für $a$ . (Bezeichnung gemäß Material 2)

(3 BE)

4.2

Leite aus der Skizze in Material 2 folgenden Zusammenhang der Größen $r$ , $a$ und $h$ her:

$r=\dfrac{a^2+h^2}{2h}$

(3 BE)

4.3

Der Graph der Funktion $k$ mit $k(x)=\sqrt{r^2-x^2}$ bildet die Randlinie eines Halbkreises mit dem Radius $r$ und dem Mittelpunkt im Ursprung des Koordinatensystems. Erkläre die Bedeutung der Zeilen (1) bis (3) und deute das Ergebnis für $K$ im Sachzusammenhang.

(1)

$K=\pi\cdot\displaystyle\int_{r}^{r-h}\left(r^2-x^2\right)dx$

(2)

$K=\pi\cdot h^2\cdot\left(r-\dfrac{h}{3}\right)$

(3)

$K=\pi\cdot h^2\cdot\left(\dfrac{a^2+h^2}{2\cdot h}-\dfrac{h}{3}\right)$

(7 BE)

Material 1

$P_1(0\mid 2,5),$ $P_2(5\mid 2,5),$ $P_3(20\mid 15)$ und $P_4(40\mid 15)$

Material 2

Bildunterschrift

$\begin{array}[t]{rll} A_1 &=& 2\cdot 42\cdot y_{P_1} \\[5pt] &=& 2\cdot 42 \cdot 2,5 \\[5pt] &=& 210\,\left[\text{cm}^2\right] \\[5pt] \end{array}$

$A_2 =93,75\,\left[\text{cm}^2\right]$

Rechenweg anzeigen

$A_3= 273\,\left[ \text{cm}^2\right]$

Rechenweg anzeigen

Für den Gesamtflächeninhalt folgt:

$A= 943,5\, \left[ \text{cm}^2\right]$

Rechenweg anzeigen

Der Inhalt der Querschnittsfläche des befüllbaren Bereichs beträgt $943,5\,\text{cm}^2.$

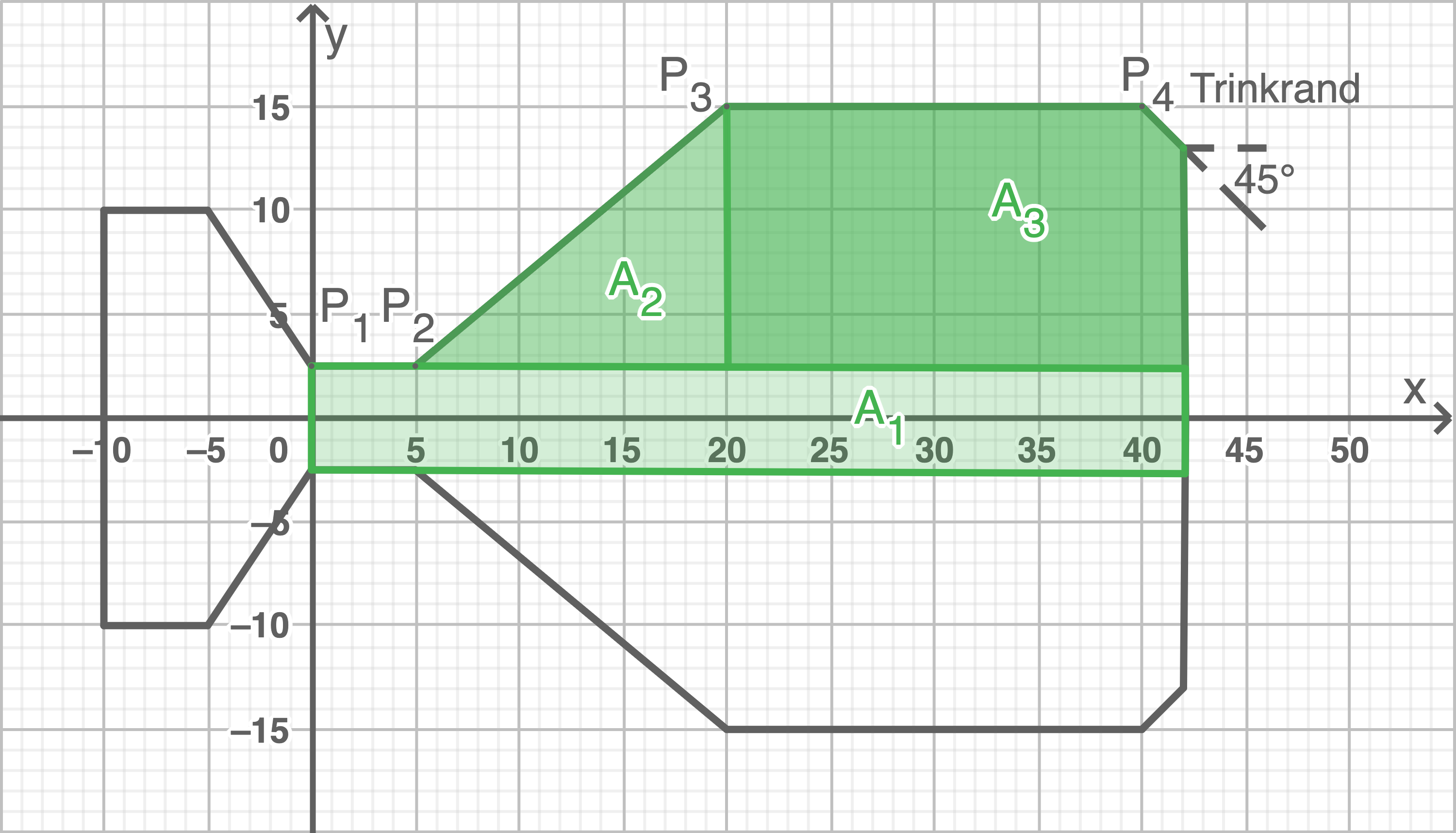
Hilfsskizze

2.1

Funktionsgleichung ermitteln

Ganzrationale Funktion anzeigen

Durch Einsetzen der gegebenen Koordinaten in die Funktion $f$ ergibt sich folgendes Gleichungssystem:

Gleichungssystem anzeigen

Damit der Winkel am Trinkrand $45^{\circ}$ beträgt, muss gelten:

$\(f$

Es gilt: $\(f$

Somit folgt die fünfte Gleichung des LGS:

Gleichung anzeigen

Mit dem CAS kann das Gleichungssystem nun gelöst werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 3: Algebra $\to$ 7

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math1 $\to$ $\{^{\Box}_{\Box}$

Es ergeben sich folgende Werte für die Parameter:

$\begin{array}[t]{rll} a &\approx& 0,000027 \\[5pt] b &\approx& -0,003386 \\[5pt] c &\approx& 0,112186 \\[5pt] d &\approx& -0,479649 \\[5pt] e &=& 2,5 \end{array}$

Eine ganzrationale Funktion vierten Grades ist somit gegeben durch:

$f(x)=...$

Vollständige Funktion anzeigen

Mindestgrad begründen

Da die Funktion verschiedene Funktionswerte annehmen muss, kann sie schon einmal nicht vom Grad Null sein.

Da aber trotzdem beispielsweise in den Punkten $P_1$ und $P_2$ der gleiche Funktionswert angenommen werden soll, muss zwischen diesen beiden Punkten ein Extrempunkt liegen. Gleiches gilt für die beiden Punkte $P_3$ und $P_4.$

Die Funktion $f$ muss also mindestens dritten Grades sein. Zusammen mit dem geforderten Winkel am Trinkrand, ergibt sich ein Gleichungssystem, das für eine Funktion dritten Grades nicht lösbar ist. Sie muss also mindestens vierten Grades sein.

2.2

Mit der Formel für das Volumen von Rotationskörpern gilt:

$V = \pi \cdot \displaystyle\int_{0}^{42}(f_E(x))^2\;\mathrm dx$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

Mit dem CAS folgt:

$\begin{array}[t]{rll} V&\approx& 25\,811\,\left[\text{cm}^3 \right] \end{array}$

Bei Verwendung der Funktion $f$ ergibt sich für den befüllbaren Bereich ein Gesamtvolumen von ca. $25\,811\,\text{cm}^3.$

3.1

Überlegungen erläutern

(1)

Die Nullstellen von $\(f$ sind die Stellen, an denen das notwendige Kriterium für lokale Extremstellen von $f$ erfüllt ist. In diesem Schritt werden also die lokalen Extremstellen von $f$ bestimmt.

(2)

Die Funktionswerte an diesen beiden Nullstellen entsprechen nun den $y$ -Koordinaten der Extrempunkte von $f.$

(3)

Der Parameter $c$ beschreibt die Verschiebung des Graphen entlang der $y$ -Achse. Ist der Graph einer trigonometrischen Funktion nicht verschoben, ist also $c=0,$ so sind die $y$ -Koordinaten aller Extrempunkte betragsmäßig gleich. Die Tiefpunkte liegen dann unterhalb der $x$ -Achse, die Hochpunkte oberhalb der $x$ -Achse.
Durch die Mittelwertbildung der $y$ -Koordinate der beiden Extrempunkte des Graphen von $f$ wird $c$ so gewählt, dass die Hoch- und Tiefpunkte des Graphen von $s$ denen von $f$ entsprechen.

Bestimmung von $k$ erläutern

Der Parameter $k$ hängt von der Periodenlänge der Funktion $s$ ab. Die halbe Periodenlänge von $s$ ist der Abstand zweier aufeinanderfolgender Extremstellen.

Es muss also die Differenz $d$ der beiden in (1) bestimmten Nullstellen von $\(f$ bestimmt werden. Die Periodenlänge von $s$ ist dann $p=2\cdot d.$

Mithilfe der Formel $k = \dfrac{2\pi}{p}$ kann aus der Periodenlänge anschließend der Parameter $k$ bestimmt werden:

3.2

Aus der Periodenlänge $p$ erhält man:

$k= \dfrac{2\pi}{p} = \dfrac{2\pi}{55,7613} \approx 0,113$

$s(x)=...$

Vollständige Funktion anzeigen

Eine Stammfunktion von $s$ ist somit gegeben durch:

$S(x)=...$

Vollständige Stammfunktion anzeigen

Der Flächeninhalt zwischen der Funktion $s$ und der $x$ -Achse entspricht der halben Querschnittsfläche. Somit folgt:

$A_s \approx 1004,1\,\left[\text{cm}^2\right]$

Rechenweg anzeigen

Durch die Modellierung mit der Funktion $s$ erhält man für den Flächeninhalt der Querschnittsfläche des befüllbaren Bereichs des Pokals ca. $1004,1\,\text{cm}^2.$

3.3

Der in Aufgabe 1 ermittelte Flächeninhalt beträgt $943,5 \,\left[\text{cm}^2 \right].$

Relative Abweichung der Funktion $f:$

$A_f \approx 1048,4 \,\left[\text{cm}^2 \right]$

Rechenweg anzeigen

$\begin{array}[t]{rll} r_f&=& \dfrac{1048,4}{943,5} \\[5pt] &\approx& 1,1112 \\[10pt] \end{array}$

Relative Abweichung der Funktion $s:$

$\begin{array}[t]{rll} r_s &=& \dfrac{1004,1}{943,5} \\[5pt] &\approx& 1,0642 \\[10pt] \end{array}$

Die größere relative Abweichung des Flächeninhalts der Querschnittsfläche tritt also bei der Modellierung mit der Funktion $f$ auf.

4.1

Der Parameter $a$ beschreibt den Radius der Kugelkappe am Deckelrand.

Dieser muss dem Radius des Pokalrandes entsprechen, welcher der $y$ -Koordinate an der Stelle $x=42$ entspricht.

Somit folgt:

$a=s(42)\approx 13,15\,\left[ \text{cm}^2\right]$

4.2

Die Länge der vom Mittelpunkt ausgehenden -in der Skizze gestrichelt dargestellten- Linie beträgt $r-h.$ Die Strecken mit den Längen $a,$ $r$ und $r-h$ bilden ein rechtwinkliges Dreieck.

Mit dem Satz des Pythagoras folgt:

$(r-h)^2 +a^2 = r^2$

Rechenweg anzeigen

Somit folgt der Zusammenhang $r =\dfrac{a^2+h^2}{2h}.$

4.3

(1)

Es wird das Volumen des Rotationskörpers berechnet, der entsteht, wenn die Fläche, die die beschriebene Randlinie des Halbkreises mit der $x$ -Achse im Bereich $r-h\leq x \leq r$ einschließt, um die $x$ -Achse rotiert.

(2)

Das Integral wird mithilfe einer Stammfunktion von $k^2 = r^2-x^2$ umgeformt.

(3)

Der Zusammenhang aus 4.2 wird ausgenutzt. Für $r$ wird daher $r= \dfrac{a^2+h^2}{2h}$ eingesetzt. Der Term hängt also nur noch von $h$ und $a$ ab, nicht mehr direkt von $r.$

$K$ entspricht dem Volumen des Deckels in Form einer Kugelkappe. Der Term für das Volumen wurde soweit vereinfacht, dass dazu nicht in einem Zwischenschritt der Radius der zugehörigen Kugel berechnet werden muss, sondern direkt die Maße $a$ (Radius des Querschnitts der Pokalöffnung) und $h$ (Höhe des Deckels) verwendet werden können. Das Volumen des Deckels hängt also nicht vom Radius der zugehörigen Kugel ab.