B2 – Analysis

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_k$ mit $f_k(x)=\frac{1}{2 k} \cdot x^2 \cdot(x-2 k)^2$ und $k \in \mathbb{R}^{+}.$ Der Graph von $f_k$ wird mit $G_k$ bezeichnet.

1.1

Begründe, dass $f_k$ für jeden Wert von $k$ genau zwei Nullstellen hat, und gib diese an.

(3 BE)

1.2

Der Hochpunkt von $G_k$ hat zu den beiden Tiefpunkten von $G_k$ denselben Abstand. Bestimme diesen Abstand.

(4 BE)

1.3

Betrachtet wird die Fläche, die $G_k,$ die $x$ -Achse und die beiden Geraden mit den Gleichungen $x=-1$ und $x=1$ einschließen. Sie setzt sich aus mehreren Flächenstücken zusammen. Beurteile die folgende Aussage, ohne den Wert eines Integrals zu berechnen:

Für jeden Wert von $k$ gibt der Term $\displaystyle\int_{-1}^{1}f_k(x)\;\mathrm dx$ den Inhalt der betrachteten Fläche an.

(4 BE)

1.4

Für jeden Wert von $k$ schließen $G_k$ und der Graph der in $\mathbb{R}$ definierten Funktion $h_k$ mit $h_k(x)=\frac{k}{2} \cdot(x-2 k)^2$ eine Fläche ein, die sich aus zwei Flächenstücken zusammensetzt. Untersuche, ob die folgende Aussage richtig ist: Für $k\gt3$ ist der Inhalt der Fläche kleiner als $k^5.$

(5 BE)

Um Regenwasser zu speichern, wird es kontrolliert in ein unterirdisches Auffangbecken geleitet. Für ein bestimmtes Regenereignis wird die momentane Zuflussrate des Regenwassers in das Auffangbecken durch die in $\mathbb{R}$ definierte Funktion $r$ mit $r(x)=\mathrm e^x \cdot f_{2,5}(x)$ für $0 \leq x \leq 5$ modellhaft beschrieben. Dabei ist $x$ die Zeit in Stunden, die seit Beginn des Zuflusses in das Auffangbecken vergangen ist, und $r(x)$ die momentane Zuflussrate in $\frac{m^3}{h}$ (Kubikmeter pro Stunde). Die Funktion $f_{2,5}$ ist die Funktion der Schar aus Aufgabe 1 mit $k=2,5.$

2.1

Bestimme die größte und die kleinste momentane Zuflussrate im betrachteten Zeitraum.

(4 BE)

2.2

Im Intervall $[0 ; 5]$ besitzt r genau zwei Wendestellen $x_0$ und $x_1.$
Außerdem gilt $\(r$ und $\(r$ sowie $\(r$ und $\(r$
Beschreibe die Bedeutung des Wertes $\(r$ die sich aus diesen Informationen ergibt, im Sachzusammenhang.

(3 BE)

2.3

Die Abbildung zeigt den Graphen von $r$ mit einigen Eintragungen.

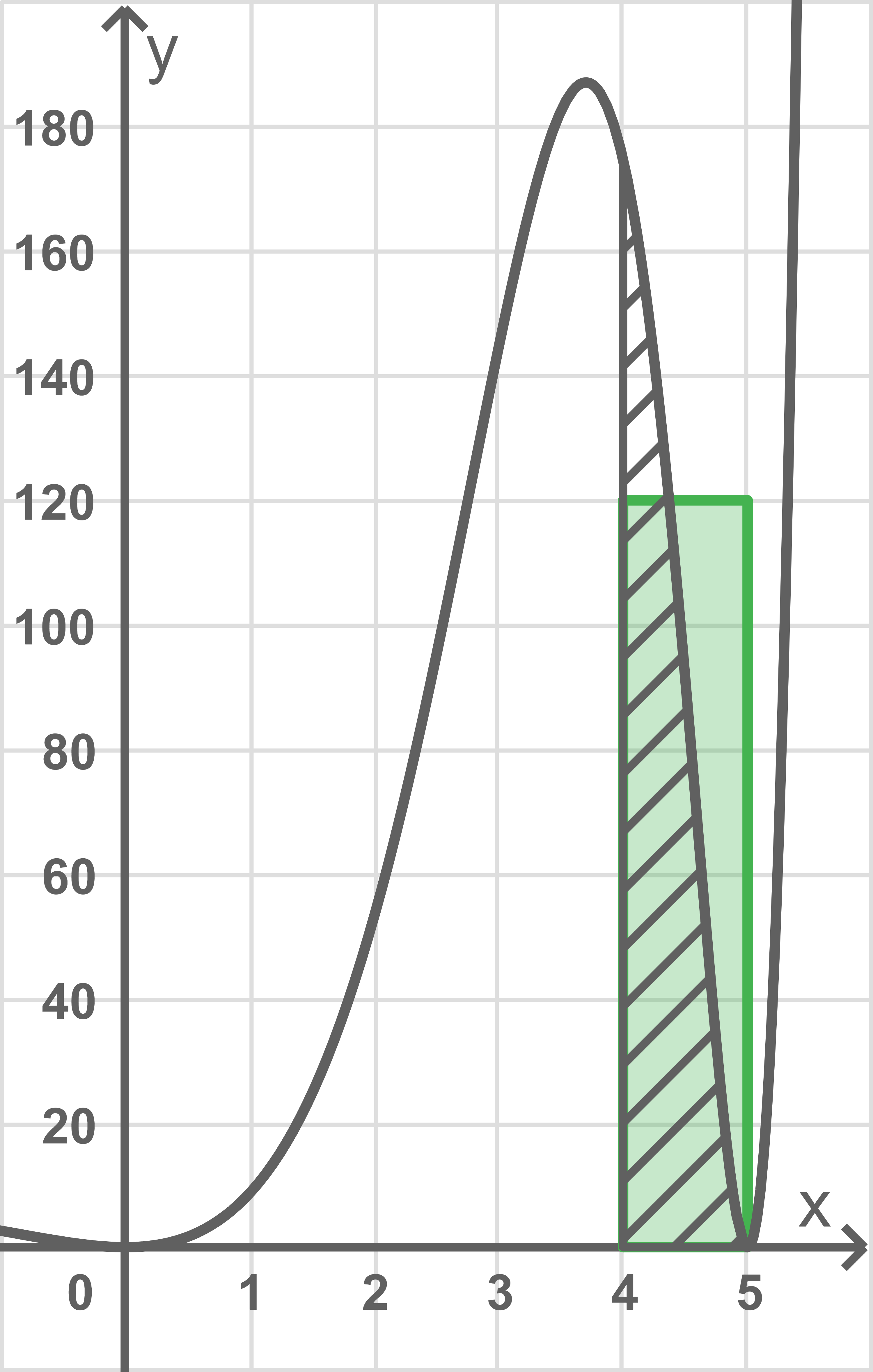
Erläutere, dass mit diesen Eintragungen die folgende Aussage begründet werden kann:

$\displaystyle\int_{4}^{5}r(x)\;\mathrm dx\lt120$

Interpretiere diese Aussage im Sachzusammenhang.

(4 BE)

2.4

Zu Beginn des Zuflusses ist das Auffangbecken bereits mit $186\;\text{m}^3$ Regenwasser gefüllt. Nach dreieinhalb Stunden wird eine Pumpe eingeschaltet. Diese pumpt bis zum Ende des betrachteten Zeitraums Wasser aus dem Auffangbecken mit einer konstanten Rate ab. Die momentane Zuflussrate des Regenwassers in das Auffangbecken wird dabei weiterhin durch $r$ beschrieben.
Gib einen Term an, der das Wasservolumen im Auffangbecken zu einem beliebigen Zeitpunkt nach dem Einschalten der Pumpe in Kubikmetern beschreibt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Nach dem Satz des Nullprodukts ergeben sich die Nullstellen von $f_k$ durch die Nullstellen der einzelnen Faktoren der Funktionsgleichung.
Der Faktor $\frac{1}{2k}$ wird für keinen Wert von $k$ Null, der Faktor $x^2$ besitzt die Nullstelle $x=0,$ und der letzte Faktor $(x-2k)^2$ wird genau dann Null, wenn die Klammer null ergibt, also für $x=2k.$
Da $k$ nur positive Werte annimmt, besitzt $f_k$ für jeden Wert von $k$ somit genau $2$ Nullstellen.

1.2

Für die erste Ableitung von $f_k$ folgt mit dem CAS:

$\(f_k$

Mit dem solve-Befehl des CAS liefert die notwendige Bedingung von Extremstellen $\(f_k$

$\begin{array}[t]{rlll} x_1&=&0 \\[5pt] x_2&=&k \\[5pt] x_3&=&2k \end{array}$

Da zwischen zwei Tiefpunkten immer ein Hochpunkt liegen muss und insgesamt drei Extrempunkte vorliegen, folgt, dass $x_2=k$ zum Hochpunkt von $G_k$ gehört. Damit folgt für de gesuchten Abstand $d$ mit dem CAS:

Rechenweg anzeigen

$d = k\cdot\sqrt{1+\dfrac{1}{4}k^4}$

1.3

Der Funktionsterm von $f_k$ besteht aus drei Faktoren, wobei $\frac{1}{2k}$ für alle $k$ positiv ist da $k$ stets positiv ist, und die anderen beiden nicht negativ sind, da sie geradzahlige Exponenten besitzen. Somit verläuft $G_k$ nie unterhalb der $x$ -Achse, d.h. die Aussage aus der Aufgabenstellung stimmt.

1.4

Mit dem solve-Befehl des CAS liefert $f_k(x)=h_k(x):$

$\begin{array}[t]{rlll} x_1&=&-k \\[5pt] x_2&=&k \\[5pt] x_3&=&2k \end{array}$

Mit der graphischen Darstellung des CAS folgt zudem, dass der Graph von $h_k$ zwischen $x_1$ und $x_2$ oberhalb, und zwischen $x_2$ und $x_3$ unterhalb des Graphen von $f_k$ verläuft. Somit folgt für den Inhalt $A$ der gesuchten Fläche mit dem CAS:

Rechenweg anzeigen

$A = \dfrac{29}{10}k^4$

Damit folgt:

$\begin{array}[t]{rlll} \dfrac{29}{10}k^4&\lt&k^5 &\mid\;:k^4 \\[5pt] \dfrac{29}{10}&\lt&k \end{array}$

Da $\frac{29}{10}\lt3$ gilt, ist die Aussage aus der Aufgabenstellung somit richtig.

2.1

Die Funktion $r(x)$ ergibt sich als:

$r(x)=\mathrm e^x\cdot\dfrac{1}{5}x^2\cdot(x-5)^2$

Damit folgt für die Ableitung von $r$ mit Hilfe des CAS:

$\(r$

Die Notwendige Bedingung für Extremstellen $\(r$ liefert mit dem solve-Befehl des CAS für $0\leq x\leq5:$

$\begin{array}[t]{rlll} x_1&=&0 \\[5pt] x_2&=&\dfrac{1+\sqrt{41}}{2} \\[5pt] x_3&=&5 \end{array}$

Nach Teilaufgabe 1.1 gilt $r(0)=0$ und $r(5)=0.$ Einsetzen von $x_2$ in $r(x)$ liefert:

Rechenweg anzeigen

$r\left(\dfrac{1+\sqrt{41}}{2}\right) \approx 187$

Da die Funktionswerte für sowohl $x_1$ als auch $x_3$ kleiner als $187$ sind, folgt, dass es sich bei $x_2$ um eine Hochstelle von $r$ handelt und zudem, dass $r$ an den Stellen $x=0$ und $x=5$ seinen im betrachteten Bereich minimalen Wert annimmt.

Die kleinste momentane Zuflussrate beträgt somit $0\;\frac{\text{m}^3}{\text{h}}$ und die größte ca. $187\;\frac{\text{m}^3}{\text{h}}.$

2.2

Der stärkste Anstieg der momentanen Zuflussrate im betrachteten Zeitraum ist durch $\(r$ pro Stunde gegeben.

2.3

Begründung der Aussage erläutern

Die in der Abbildung grün markierte Fläche ist ein Rechteck mit den Seitenlängen $1$ und $120$ und besitzt somit den Flächeninhalt $120.$ Zudem wird aus der Abbildung deutlich, dass die schraffierte Fläche, deren Inhalt dem Wert des in der Aufgabenstellung gegebenen Integrals entspricht, kleiner ist, als die grün markierte Fläche. Damit kann die Aussage aus der Aufgabenstellung begründet werden.

Aussage im Sachzusammenhang interpretieren

Innerhalb der letzten Stunde des betrachteten Zeitraums sind insgesamt weniger als $120\;\text{m}^3$ Regenwasser in das Auffangbecken geflossen.

2.4

Die Pumpe pumpt Wasser mit einer konstanten Rate ab. Wenn diese Rate mit $a$ bezeichnet wird, folgt für den gesuchten Term:

$186+\displaystyle\int_{0}^{x}r(t)\;\mathrm dx-a\cdot(x-3,5)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?