B1 - Analysis

Biologen untersuchen eine Bakterienkultur unter Laborbedingungen. Es kann festgestellt werden, dass sich die Entwicklung der Anzahl der Bakterien sehr gut durch die Funktion $f$ mit

$f(t)=\dfrac{4\cdot 10^6}{1+1000\cdot \mathrm{e}^{-2t}},$ $t\geq0,$ beschreiben lässt.

Dabei ist $t$ die Zeit in Stunden nach Beobachtungsbeginn und $f(t)$ ist die Anzahl der Bakterien.

1.1

Zeige rechnerisch, dass die Funktion $f$ auch durch die Funktionsgleichung

$f(t)=\dfrac{4\cdot 10^6\cdot \mathrm{e}^{2t}}{1000 + \mathrm {e}^{2t}}$ beschrieben werden kann.

(2 BE)

1.2

Gib die erste Ableitung der Funktion $f$ an und erkläre deren Bedeutung im Sachzusammenhang.

(2 BE)

1.3

Gib die Werte der Funktion $f$ sowie ihrer Ableitung $\(f$ zu Beobachtungsbeginn sowie $1,$ $2,$ $3,$ $4,$ $5$ und $6$ Stunden nach Beobachtungsbeginn in einer Wertetabelle an.
Zeichne die Graphen der Funktion $f$ sowie ihrer Ableitung $\(f$ in ein geeignetes Koordinatensystem.

(7 BE)

1.4

Bestimme den Zeitpunkt, an dem die Bakterienkultur am schnellsten wächst, und gib die maximale Wachstumsgeschwindigkeit an.

Hinweis: Die Überprüfung der notwendigen Bedingung ist ausreichend.

Bestimme die mittlere Wachstumsgeschwindigkeit im Intervall $[0;6].$

(6 BE)

1.5

Bestimme die Anzahl der Bakterien, der sich die Bakterienkultur langfristig annähert, und ermittle den Zeitpunkt, an dem die Bakterienkultur $95$ $\,\%$ dieser Anzahl erreicht.

(4 BE)

1.6

Die Biologen interessieren sich nicht nur für die Anzahl der Bakterien zu einem bestimmten Zeitpunkt, sondern auch für den Zuwachs an Bakterien über einen gewissen Zeitraum. Erkläre, warum das Integral $\(\displaystyle\int_{t_2}^{t_1}f$ mit $t_1 \gt t_2$ diesen Zuwachs angibt.

(3 BE)

Biologen verwenden zur Modellierung von Wachstumsprozessen häufig logistische Funktionen. Diese sind Funktionen vom Typ:

$h_{a,S,k}(t)=\dfrac{S\cdot \mathrm e^{kt}}{a+\mathrm e^{kt}}$ , $a, S, k \gt0$

2.1

Die Funktion $f$ aus Aufgabe 1 ist eine Funktion dieses Typs. Gib die Zahlenwerte von $a,$ $S$ und $k$ für die in Aufgabe 1 betrachtete Bakterienkultur an.

(3 BE)

2.2

Bestimme den Wendepunkt der Funktionenschar $h_{a,S,k}$ und die Steigung an der Wendestelle in Abhängigkeit von den Parametern $a,$ $S$ und $k.$
Gib die Bedeutung des Parameters $S$ bezogen auf das Wachstum an und beschreibe den Einfluss des Parameters $k$ auf die Wachstumsgeschwindigkeit im Wendepunkt.

(6 BE)

Für die folgenden Aufgaben wird die Funktionenschar $f_a$ eines Wachstumsprozesses in der Darstellung $f_a(t)=\dfrac{4\cdot 10^6\cdot \mathrm e^{2t}}{a+\mathrm e^{2t}}$ , $a\gt 0, t\geq 0,$ betrachtet.

2.3

Berechne einen Term, mit dem für einen gegebenen Anfangswert $f_a(0)=C$ der Parameter $a$ ermittelt werden kann.

(3 BE)

2.4

Untersuche das Monotonieverhalten der Funktionenschar $f_a$ und gib den Wertebereich von $f_a$ in Abhängigkeit von $a$ als Intervall an.

(4 BE)

Zur Modellierung der Entwicklung der Bakterienanzahl zu Beginn des Wachstums verwenden Biologen häufig eine einfache Exponentialfunktion.

3.1

Ermittle aus den beiden Punkten $P_1(0\mid f(0))$ und $P_2(3\mid f(3))$ eine Exponentialfunktion $g$ der Form $g(t)=b\cdot \mathrm e^{c\cdot t}.$ Verwende dazu den Funktionsterm $f(t)=\dfrac{4\cdot10^6}{1+1000\cdot \mathrm e^{-2t}}$ aus Aufgabe 1.

(3 BE)

3.2

Es soll angenommen werden, dass die Funktion $f$ aus Aufgabe 1 den Wachstumsprozess auf dem Intervall $[0;3]$ bestmöglich modelliert. Als Maß für die Güte der Modellierung des Wachstumsprozesses durch die Funktion $g$ soll daher im Intervall $[0;3]$ die maximale Abweichung $d_{\text{max}}$ der Funktionswerte von $g$ von den Funktionswerten von $f$ an einer Stelle betrachtet werden.

Bestimme das so definierte Gütemaß $d_{\text{max}}$ sowie die zugehörige prozentuale Abweichung der Funktionswerte der beiden Funktionen bezogen auf den Wert der Funktion $f$ an der zugehörigen Stelle $t_{\text{max}}$ .
Falls du die Funktion $g$ in Aufgabe 3.1 nicht bestimmen konntest, verwende stattdessen die Ersatzfunktion $g_E$ mit $g_E(t)=4000\cdot \mathrm e^{1,89t}$ .

(7 BE)

1.1

Durch Erweitern des Bruches mit $\mathrm e^{2t}$ folgt:

Rechenweg anzeigen

$f(t)=\dfrac{4\cdot 10^6\cdot \mathrm e^{2t}}{1000+\mathrm e^{2t}}$

1.2

Erste Ableitung bestimmen

Mit der Quotientenregel folgt:

$u(x)=4\cdot 10^6\cdot \mathrm e^{2t}$

$v(x)=1000+\mathrm e^{2t}$

$\(u$

$\(v$

Rechenweg anzeigen

$\( f$

Ableitung deuten

Da $f(t)$ der Anzahl der Bakterien $t$ Stunden nach Beobachtungsbeginn entspricht, beschreibt $\(f$ die momentane Änderungsrate, also die Wachstumsgeschwindigkeit, der Anzahl der Bakterien zum Zeitpunkt $t$ Stunden nach Beobachtungsbeginn.

1.3

Wertetabelle angeben

$\color{#fff}{x}$	$\color{#fff}{f(x)}$	$\(\color{#fff}{f$
$0$	$3996,00$	$7984,02$
$1$	$29339,43$	$58248,47$
$2$	$207086,08$	$392729,84$
$3$	$1149837,59$	$1638611,93$
$4$	$2995216,73$	$1504771,83$
$5$	$3826286,85$	$332338,18$
$6$	$3975573,23$	$48555,20$

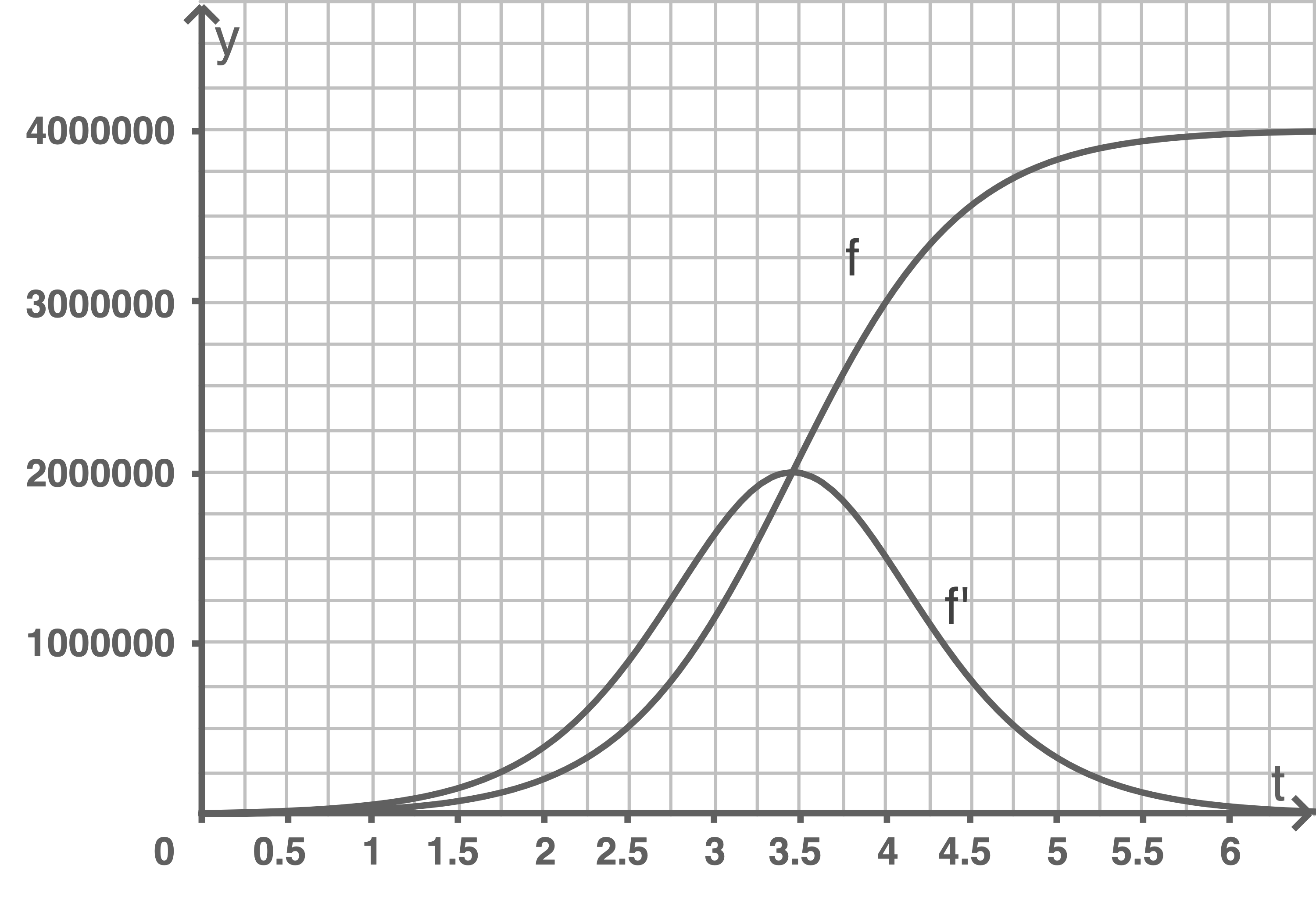
Graph von $f$ und $\(f$

1.4

Zeitpunkt bestimmen

Gesucht ist ein lokales Maximum von $\(f$

1. Schritt: Notwendige Bedingung anwenden

Für $\(f$ ergibt sich mit dem CAS:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

$\(\begin{array}[t]{rll} f$

2. Schritt: Hinreichende Bedingung prüfen

Da bereits gegeben ist, dass ein Hochpunkt existiert, und die Lösung eindeutig ist, muss die hinreichende Bedingung nicht mehr geprüft werden.

Folglich wächst die Bakterienkultur etwa $3,5$ Stunden nach Beobachtungsbeginn am stärksten.

3. Schritt: $y$ -Koordinate bestimmen

$\(f$

Die maximale Wachstumsgeschwindigkeit der Bakterienkultur beträgt also ca. $1\,999\,970\,\frac{\text{Bakterien}}{\text{h}}.$

Mittlere Wachstumsgeschwindigkeit bestimmen

Rechenweg anzeigen

$\dfrac{f(6) -f(0)}{6-0}\approx 661\;929,54$

Im Intervall $[0;6]$ beträgt die durchschnittliche Wachstumsgeschwindigkeit ca. $661\,929,54\,\frac{\text{Bakterien}}{\text{h}}.$

1.5

Langfristige Annäherung bestimmen

Wegen $\mathrm e^{-2t}\rightarrow 0$ folgt:

$\begin{array}[t]{rll} \lim\limits_{t\to\infty}f(t)&=& \lim\limits_{t\to\infty} \dfrac{4\cdot 10^6}{1+1000\cdot \mathrm e^{-2t}} & \\[5pt] &=&\dfrac{4\cdot 10^6}{1+0} & \\[5pt] &=& 4\cdot 10^6 \end{array}$

Langfristig nähert sich die Bakterienanzahl somit $4\,000\,000$ an.

Zeitpunkt ermitteln

$\begin{array}[t]{rll} f(t) &=& 0,95\cdot 4\,000\,000 & \\[5pt] \dfrac{4\cdot 10^6}{1+1000\cdot \mathrm e^{-2t}} &=& 3\, 800\,000 \end{array}$

Mit dem solve-Befehl des CAS folgt $t \approx 4,93.$

Nach etwa $5$ Stunden hat die Bakterienanzahl bereits $95\,\%$ ihres langfristigen Näherungswertes erreicht.

1.6

Die Funktion $\(f$ beschreibt die momentane Änderungsrate der Bakterienanzahl in $\frac{\text{Bakterien}}{\text{h}},$ also wie viele Bakterien exakt zum Zeitpunkt $t$ pro Stunde hinzukommen.

Mit dem Integral wird der Inhalt der Fläche zwischen dem Graphen von $\(f$ und der $t$ -Achse im Bereich $t_1 \leq t \leq t_2$ berechnet.

Der Inhalt dieser Fläche gibt damit die Summe der momentanen Änderungsraten an, also die Gesamtsumme der hinzugekommenen Bakterien im Zeitraum von $t_1$ bis $t_2.$

2.1

Aus der Darstellung von $f(t)$ aus Aufgabe 1.1 lassen sich folgende Werte ablesen:

$S= 4\cdot 10^6$

$a= 1000$

$k = 2$

2.2

Wendepunkt bestimmen

Mit dem CAS können die ersten drei Ableitungsfunktionen von $h_{a;S;k}$ gebildet werden.

1. Schritt: Notwendiges Kriterium für Wendestellen anwenden

Mit dem CAS folgt:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

$\(\begin{array}[t]{rll} h_{a;S;k}$

2. Schritt: Hinreichende Bedingung prüfen

$\(h_{a;S;k}$

An der Stelle $t= \dfrac{\ln a}{k}$ befindet sich also die Wendestelle von $h_{a;S;k}.$

3. Schritt: $y$ -Koordinate bestimmen

$h_{a;S;k}\left(\dfrac{\ln a}{k} \right)= \dfrac{S}{2}$

Die Koordinaten des Wendepunkts lauten also $W_{a;S;k}\left(\frac{\ln a}{k}\mid \frac{S}{2}\right).$

Steigung berechnen

$\(h_{a;S;k}$

Die Steigung im Wendepunkt beträgt folglich $\frac{S\cdot k}{4}.$

Parameter deuten

$S$ gibt die Wachstumsschranke an. Dies ist der Wert, dem sich die untersuchte Größe langfristig annähert, ihn aber nicht erreicht.
Die Wachstumsgeschwindigkeit im Wendepunkt beträgt $\frac{S\cdot k}{4}.$ Je größer also der Parameter $k$ ist, desto größer ist auch die Wachstumsgeschwindigkeit im Wendepunkt.

2.3

$\begin{array}[t]{rll} f_a(0)&=& C \\[5pt] \dfrac{4\cdot 10^6\cdot \mathrm e^{2\cdot 0}}{a+\mathrm e^{2\cdot 0}}&=& C \\[5pt] \dfrac{4\cdot 10^6}{a+1}&=& C &\quad \scriptsize \mid\;\cdot (a+1) \\[5pt] 4\cdot 10^6&=& C\cdot (a+1) &\quad \scriptsize \mid\;:C \\[5pt] \dfrac{4\cdot 10^6}{C} &=& a+1 &\quad \scriptsize \mid\; -1 \\[5pt] \dfrac{4\cdot 10^6}{C} -1 &=& a \end{array}$

Für einen gegebenen Anfangswert $C$ lässt sich der Parameter $a$ also wie folgt berechnen:

$a = \dfrac{4\cdot 10^6}{C} -1$

2.4

Monotonieverhalten untersuchen

Mit dem CAS erhält man:

$\(f_a$

Für $a \gt 0$ ist sowohl der Zähler als auch der Nenner für alle $t\in \mathbb{R}$ positiv. Die Steigung von $f_a$ ist demnach für alle $a \gt 0$ und alle $t\in \mathbb{R}$ positiv.

Jede Funktion $f_a$ ist also auf ganz $\mathbb{R}$ streng monoton wachsend.

Wertebereich angeben

Da $f_a$ streng monoton wachsend ist, ist der kleinste Wert gegeben durch den Anfangsbestand:

$f_a(0)= \dfrac{4\cdot 10^6\cdot \mathrm e^{2\cdot 0}}{a+\mathrm e^{2\cdot 0}} = \dfrac{4\cdot 10^6}{a+1}$

Der größte Wert ist die Wachstumsschranke $S=4\cdot 10^6,$ deren Wert aber niemals angenommen wird. Somit folgt:

$W= \left[\frac{4\cdot 10^6}{a+1};4\cdot 10^6\right]$

3.1

Es soll gelten:

$\begin{array}{lrll} \text{I}\quad& g(0) &=& f(0) \\ \text{II}\quad& g(3) &=& f(3) \\ \end{array}$

Mit dem solve-Befehl des CAS folgt aus $\text{I}$ :

$b\approx 3996$

Durch Einsetzen von $b$ in $\text{II}$ folgt mit dem CAS:

$c \approx 1,887$

Somit ist eine Exponentialfunktion $g$ gegeben durch $g(t) \approx 3996 \cdot \mathrm e^{1,887\cdot t}.$

3.2

Gütemaß bestimmen

$d(t)= \left| f(t)-g(t) \right|$

Die maximale Abweichung $d_{max}$ entspicht dem Hochpunkt der Funktion $d(t).$

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Mit dem CAS folgt:

$\(\begin{array}[t]{rll} d$

2. Schritt: Hinreichende Bedingung prüfen

Da lediglich das Intervall $[0;3]$ betrachtet wird, bleibt nur $t_2$ zu überprüfen.

Weil $g$ so bestimmt wurde, dass $g(0)\approx f(0)$ und $g(3)\approx f(3)$ gilt, muss das Maximum bei $t\approx 2,64$ liegen.

Die hinreichende Bedingung muss somit nicht mehr rechnerisch nachgewiesen werden.

3. Schritt: $y$ -Koordinate bestimmen

$d(2,64) \approx 74\,259,33$

Das Gütemaß der Funktion $d$ auf dem Intervall $[0;3]$ beträgt also $d_{\text{max}}\approx 74\,259,33$

Prozentuale Abweichung bestimmen

$\dfrac{74\,259,33}{f(2,64)} \approx 0,1131 = 11,31\,\%$